Break the Sequential Dependency of LLM Inference Using Lookahead Decoding

Created on December 19, 2023

2023   ·   attention   decoding   llm   paper-review   transformer   ·   paper-reviews

논문 정보

  • Date: 2023-12-19
  • Reviewer: hyowon Cho
  • Property: Decoding

Introduction

많은 초거대 언어모델들이 현실 세계의 application에 적용되고 있지만, 여전히 그들의 inference는 느리고 최적화하기도 어렵다. 대다수의 언어모델들은 하나의 time step 당 하나의 토큰을 만들어내는 autoregressive decoding에 의존하고 있으며, 당연히 decoding의 수는 response 길이에 의존한다. 즉 latency도 그만큼 늘어난다는 것이다.

문제를 더욱 심각하게 만드는 것은 각 decoding step은 현대 gpu의 parallel processing power를 전혀 활용하지 못한다는 것이다. 이는 현재 긴 시퀀스를 빠르게 만들어야하는 chatbot이나 personal assistant의 큰 도전과제가 된다.

오늘 발표에서는 Vicuna와 Arena를 발표한 LMSYS의 블로그에서, 현재 자신들이 사용하는 decoding이라며 소개한 Lookahead Decoding을 다룬다. 다음의 GIF에서 확인할 수 있듯, 아주 빠른 속도로 문장을 생성해낼 수 있다.

Lookahead Decoding은 huggingface/transformers와 호환가능하며, generate 함수를 조금 수정하는 정도로 구현 가능하다. Code Repository는 다음과 같다.

Lookahead Decoding을 다루기 전에, 2023년 여러 가지 decoding technique들이 등장하면서 lookahead decoding에 기여했는데, 이들을 먼저 소개한다.

BackGround

Speculative decoding

Fast Inference from Transformers via Speculative Decoding, ICML 2023

  • guess-and-verify strategy를 소개한 논문.

  • draft model이 여러 개의 potential future token을 생성함.

  • original LLM이 병렬적으로 이 guess들을 verify.

이를 통해 decoding step의 수를 줄여 latency issue를 완화했으나, 여러 가지 한계점이 존재.

  1. draft model이 얼마나 토큰을 잘 만드느냐에 따라서 maximum speedup에 한계가 있음.
  • guess들이 다 거절 당하는 경우
  1. creating an accurate draft model is non-trivial
  • 이 draft model을 만드는 데는 extra training + tuning이 필요함.

=> Draft model을 없애보자!

Jacobi Decoding

Accelerating Transformer Inference for Translation via Parallel Decoding, ACL 2023

해당 논문의 아이디어는 Jacobi iteration method를 사용하여, Draft model없이도 parallel한 token generation이 가능해진다는 것이다.

Jacobi iteration method

Jacobi는 Ax=b 형태의 선형 연립 방정식을 구하는 방법 중 하나인데, 해의 초기값을 가정한 후 반복 계산으로 이를 수렴시키는 것이 특징이다.

즉, Ax=b를 x=Cx+d, 더 엄밀하게는, xn = Cx{n-1}+d로 정의해 x_n을 반복적으로 찾아간다. 초기값은 설정하기 나름이다.

자세한 내용은 위키피티아 참고.

Method

Greedy Search의 경우, 다음과 같이 y_i를 선택한다.

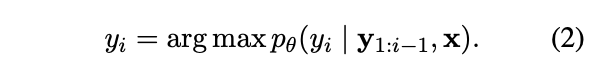
이 경우, m element를 만들기 위해, m inference steps을 sequentially 밟아야한다.

이를 해결하기 위해, 저자들은 다음과 같은 관점의 변화를 가진다. Equation (2)에 따르면, 전체 토큰에 대한 생성 절차는 다음과 같이 표현된다.

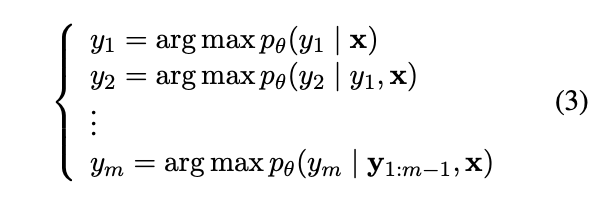
이 때, f(yi , y{1:i−1}, x) = yi − argmax pθ(yi|y{1:i−1}, x) 라고 정의하면 우리는 Equation (3)을 이렇게 다시 쓸 수 있다.

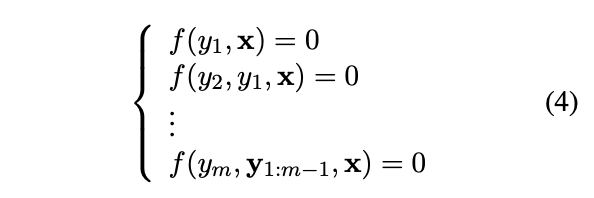
즉, 이 과정을 통해, sequential한 토큰의 생성은, 여러 개의 non-linear equations를 해결하는 시스템으로 개념화 가능하다.

구체적인 과정은 다음과 같다:

  1. Start with an initial guess for all variables [y_1, …, y_m]

  2. Calculate new y’ values for each equation with the previous y

  3. Update y to the newly calculated $y’$

  4. Repeat this process until a certain stopping condition is achieved (e.g. y’=y).

제공된 그림을 보면서 이야기해보자.

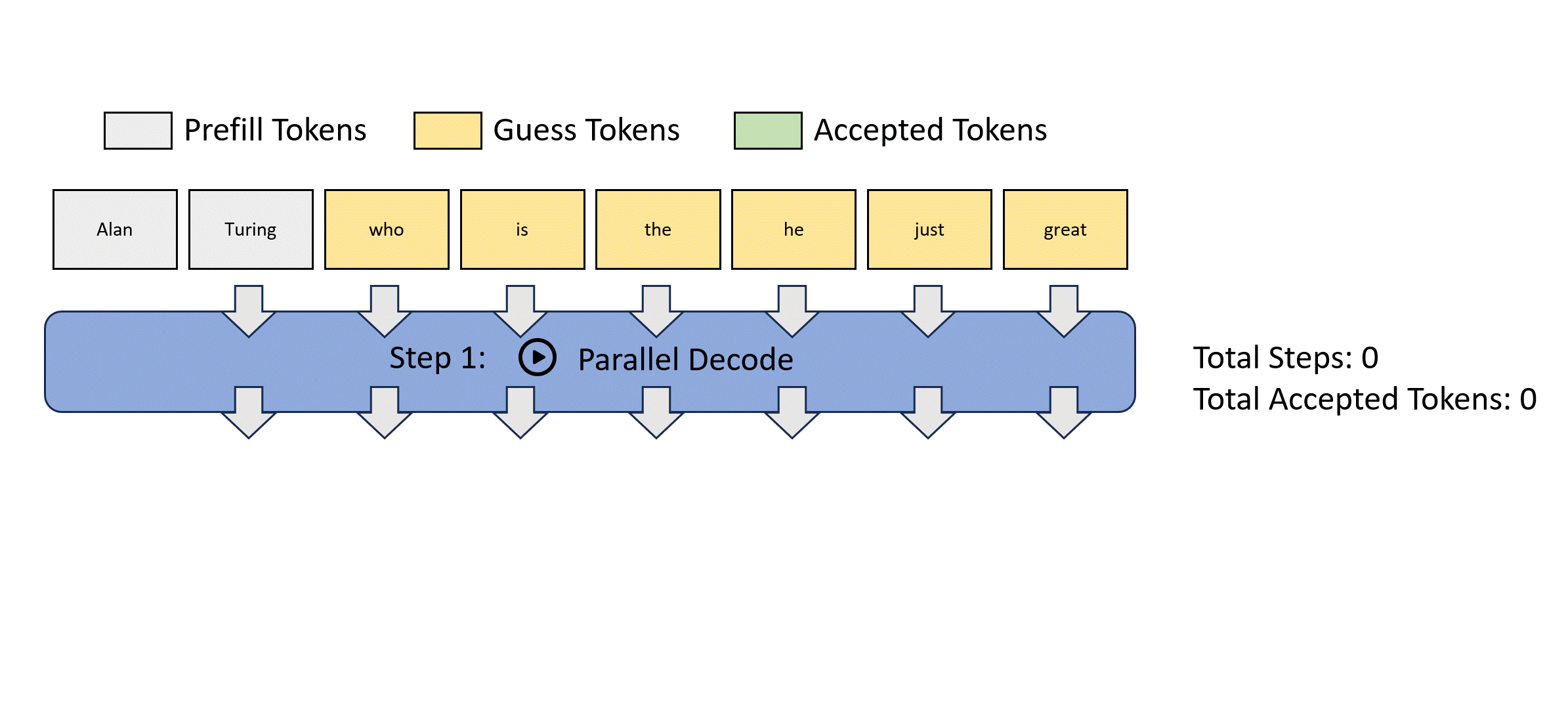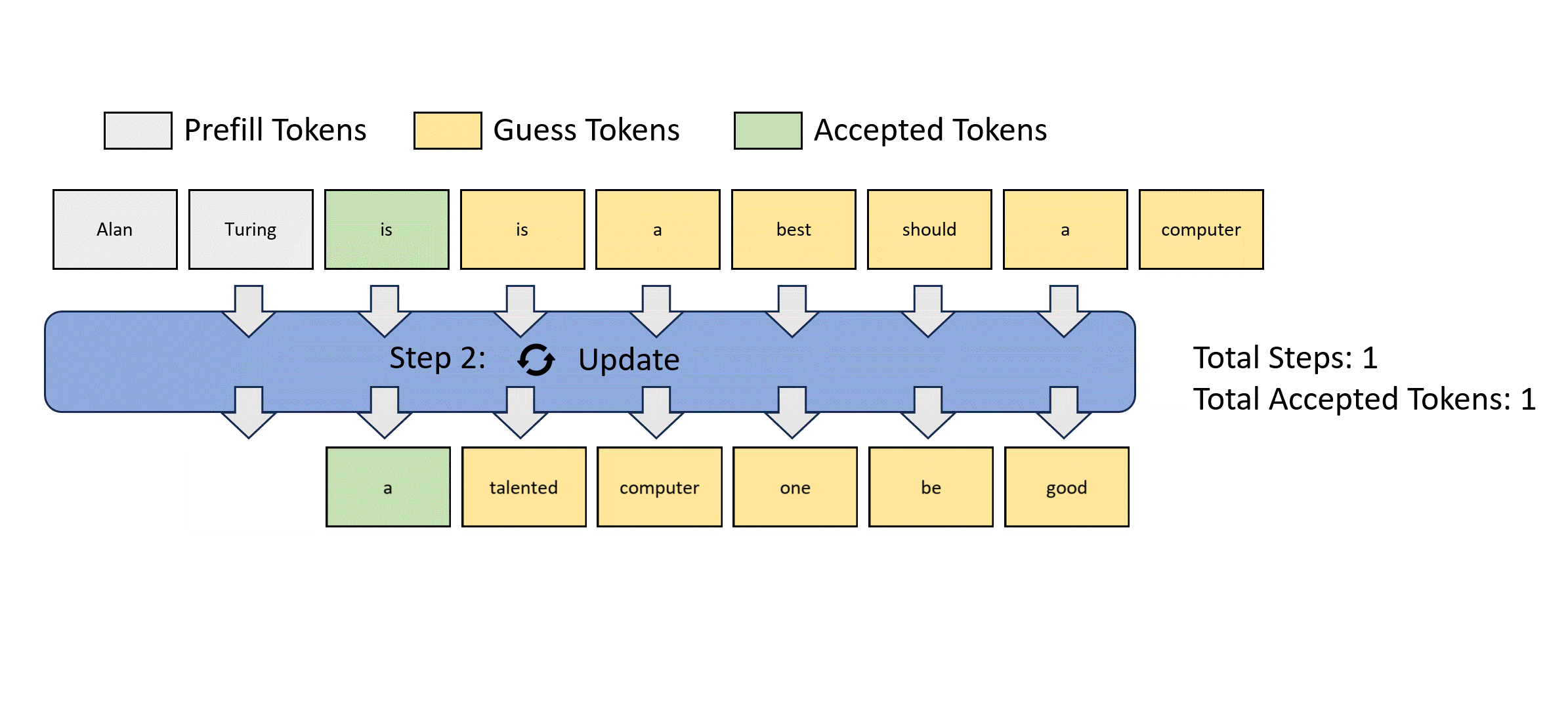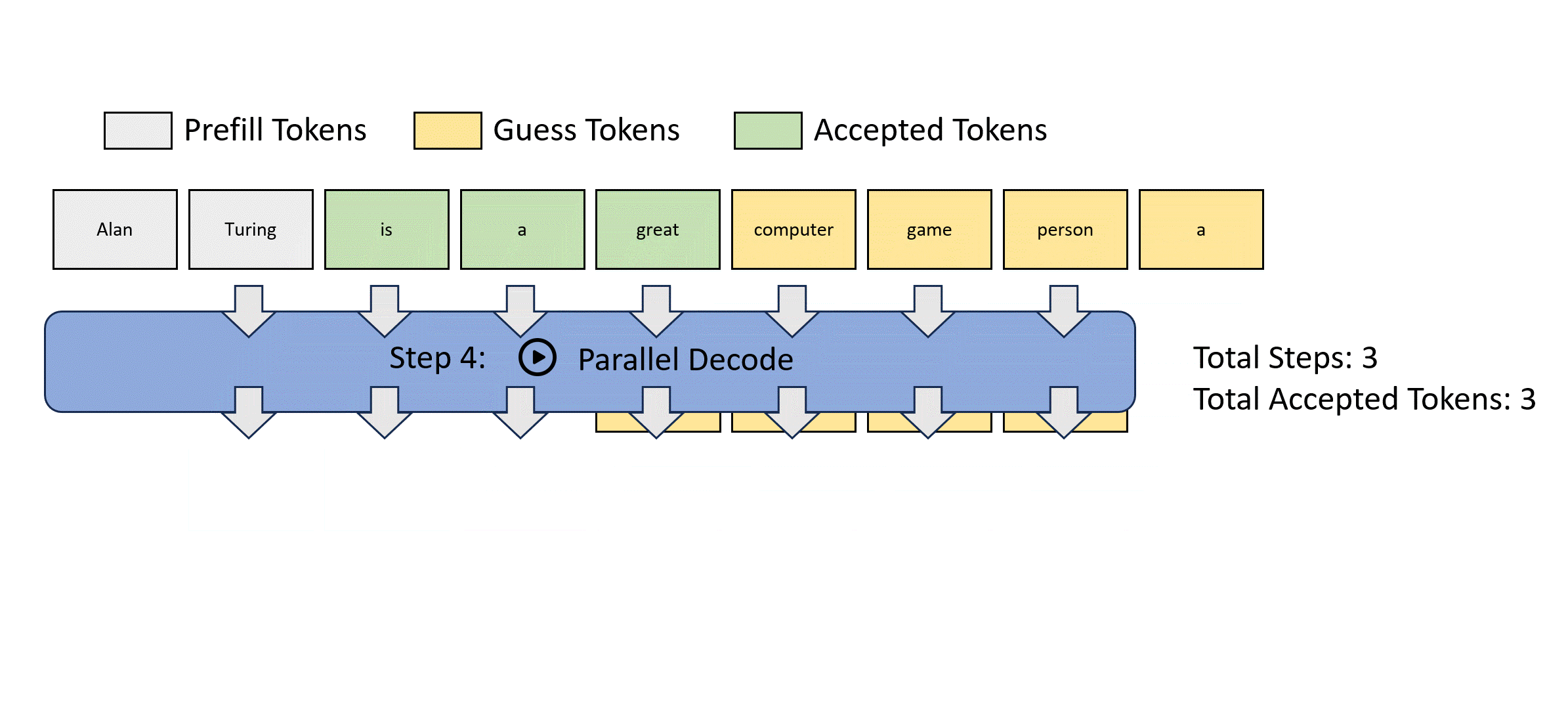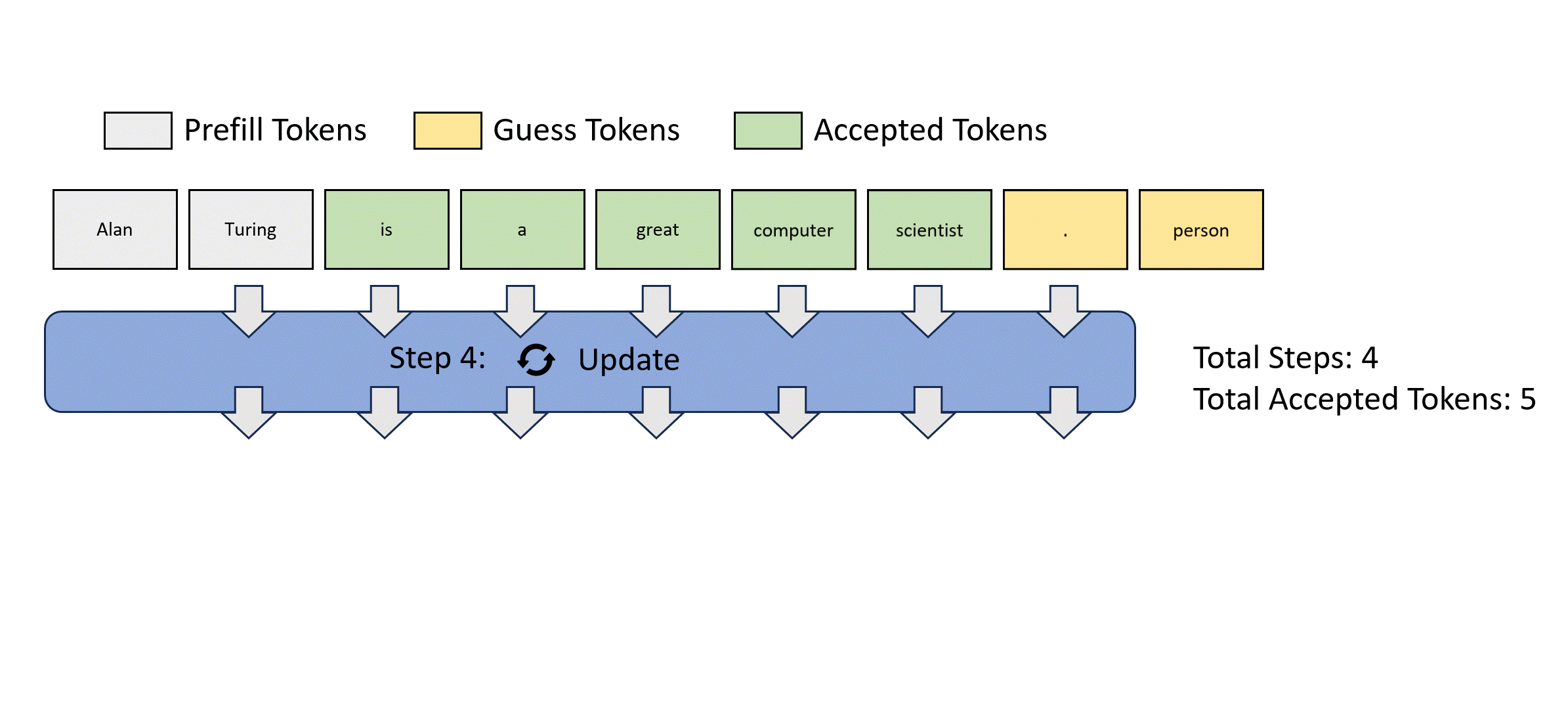
이러한 Jacobi decoding은 FLOPs의 관점에서 하나의 스텝에 더 많은 비용을 요구하지만, parallel processing을 사용할 수 있기 때문에, 속도면에서는 빨라진다.

한계점

토큰의 순서 정보를 고려하지 않기 때문에, 기존에 만들어낸 단어들이 n-gram 단위에서 옳은 애들이 있었어도 통으로 날리게 됨. 얘네들은 position의 수정만 해주면 되는 아이들임.

Lookahead Decoding

Jacobi decoding을 보면, 이전 iteration에서 다양한 n-gram historical value들이 생성되는 것을 확인할 수 있다. 예를 들어, three Jacobi iterations, a 3-gram can be formed at each token position.

Lookahead Decoding은 이렇게 생성된 n-gram을 재활용하는 모델이다. 즉, Jacobi iteration을 활용한 parallel decoding은 동일하나, future token들 뿐만이 아닌, cache에 저장된 n-gram까지 verify를 진행한다.

그림을 통해 살펴보자.

이 과정의 효율성을 높이기 위해, 하나의 lookahead decoding step은 두개의 branch로 나눠지게 된다: the lookahead branch and the verification branch.

Lookahead Branch

lookahead branch는 새로운 n-gram을 만드는 것을 목적으로 한다. 이는 fixed-sized, 2D window를 이용하는데, 각 dimension에 해당하는 파라미터는 다음과 같다:

  • window_size: how far ahead we look in future token positions

  • N-gram size: how many steps we look back into the past Jacobi iteration trajectory to retrieve n-grams.

Verification Branch

Simultaneous with lookahead branch, the verification branch selects and verifies promising n-gram candidates.

즉, 간단하게 이야기하면, n-gram의 시작 토큰이 last input token과 동일한 경우를 찾는 것. cache의 크기가 커질수록 찾는 것 자체의 비용이 커지기 때문에, 고려할 개수 G를 설정하여, W에 proportional하게 설정함.

Lookahead and Verify In The Same Step

위의 두 가지를 동시에 진행하기 위해, special attention mask를 씌움. 두 가지 규칙을 준수.

  1. The tokens in the lookahead branch cannot see tokens in the verification branch, and vice versa.

  2. Each token only sees its preceding tokens and itself as in a casual mask.

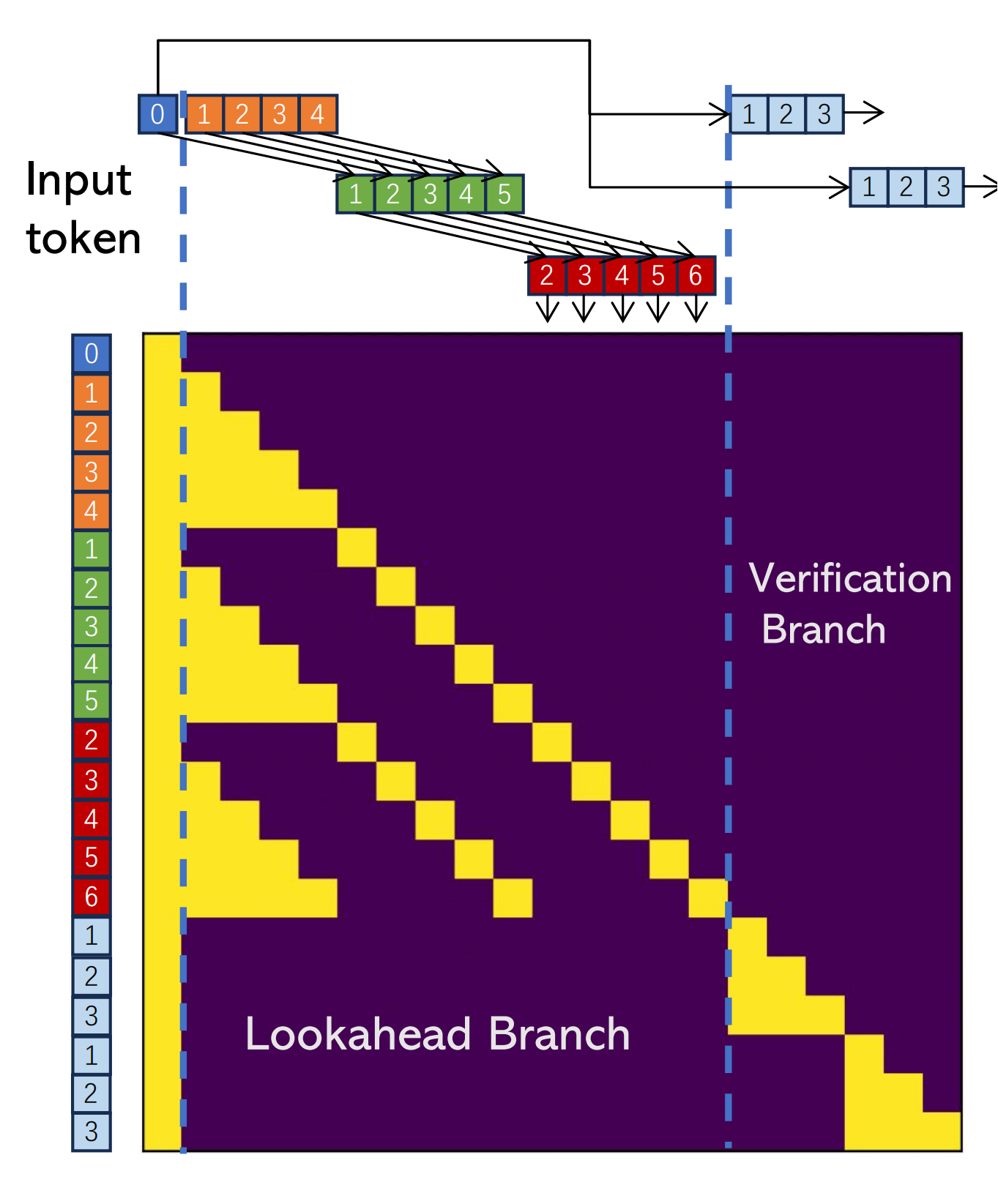
[Figure 5: Attention mask for lookahead decoding with 3-grams and window size 5. In this mask, two 3-gram candidates (bottom right) are verified concurrently with parallel decoding.]

  • blue token labeled 0 == the current input

  • orange = t-3 iteration

  • green = t-2

  • red = t-1

  • number on each token = position relative to the current input token

Scaling Law of Lookahead Decoding

W와 N의 크기가 커질수록 비용도 커짐. 하지만 이들이 커질수록, n-gram match를 통해 더 많은 단어들을 만들어낼 수 있음. 즉, lookahead decoding은 flops를 늘림으로써 latency를 줄일 수 있음.

이를 실험하기 위해, 특정 개수의 토큰들을 만들어내기 위해, 얼마만큼의 decoding stpe가 필요한지 확인해봄.

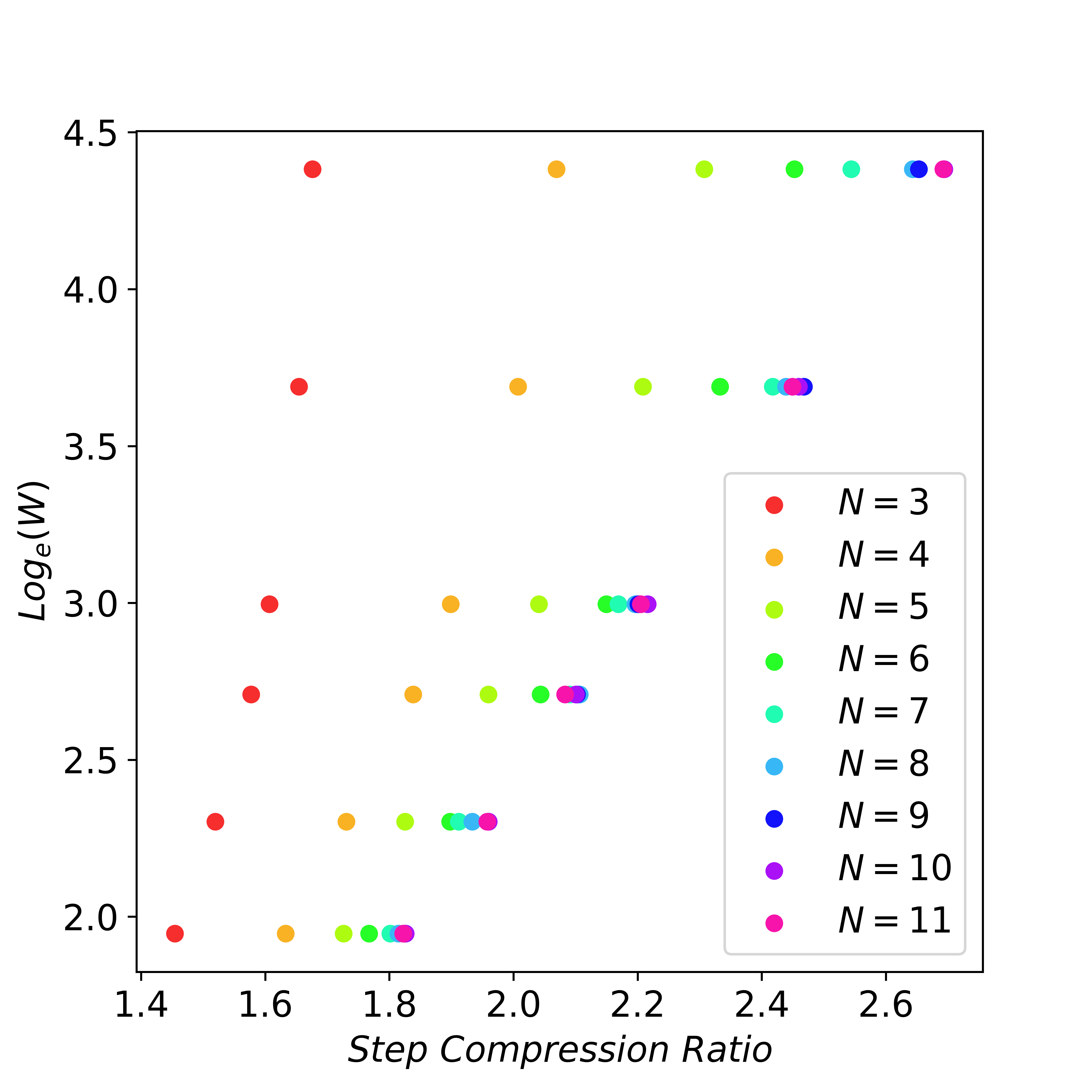
when N is large enough, an exponential increase in the W can result in a linear reduction of decoding steps.

Cost, Usage, and Limitations

For powerful GPUs (e.g., A100), lookahead decoding은 좋은 성능으로 이어질 수 있다. 하지만 여전히, W와 N이 너무 크다면, 하나의 step은 너무 느려질 것이다.

저자들을 A100에서 사용했을 때, 경험적으로 가장 좋았던 config를 공유한다.

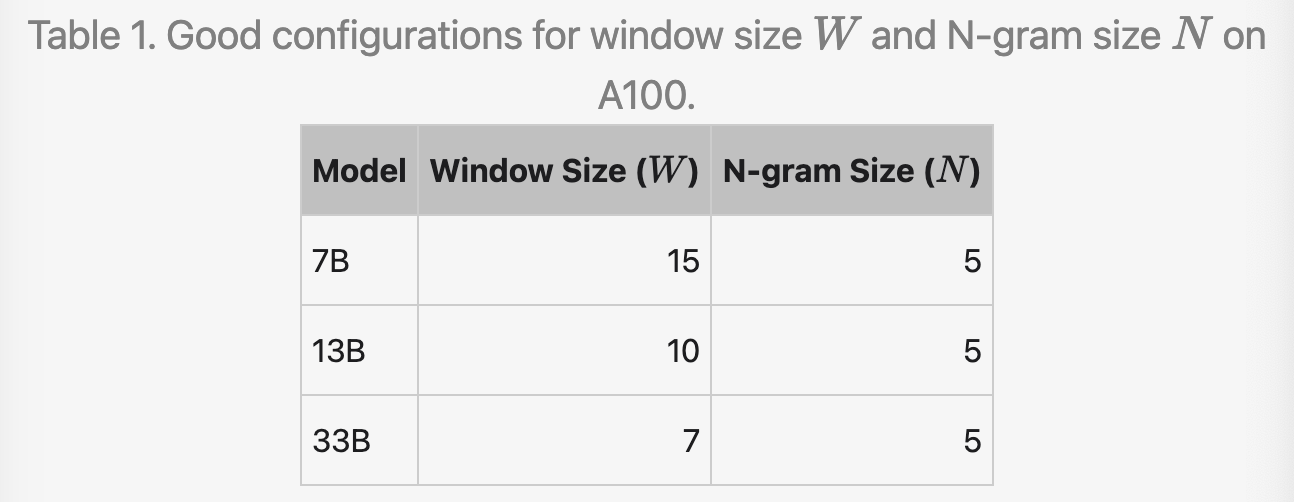
The 7B, 13B, and 33B models require 120x, 80x, and 56x extra FLOPs per step, respectively.

하지만 여전히 생각해야할 것은, 이러한 computational cost의 증가에도 불구하고 속도가 매우 빨라졌다는 것!

Experimental Result

  • 모델

    • LLaMA-2-Chat

    • CodeLLaMA

  • 데이터셋

    • MT-bench

    • HumanEval

    • GSM8K

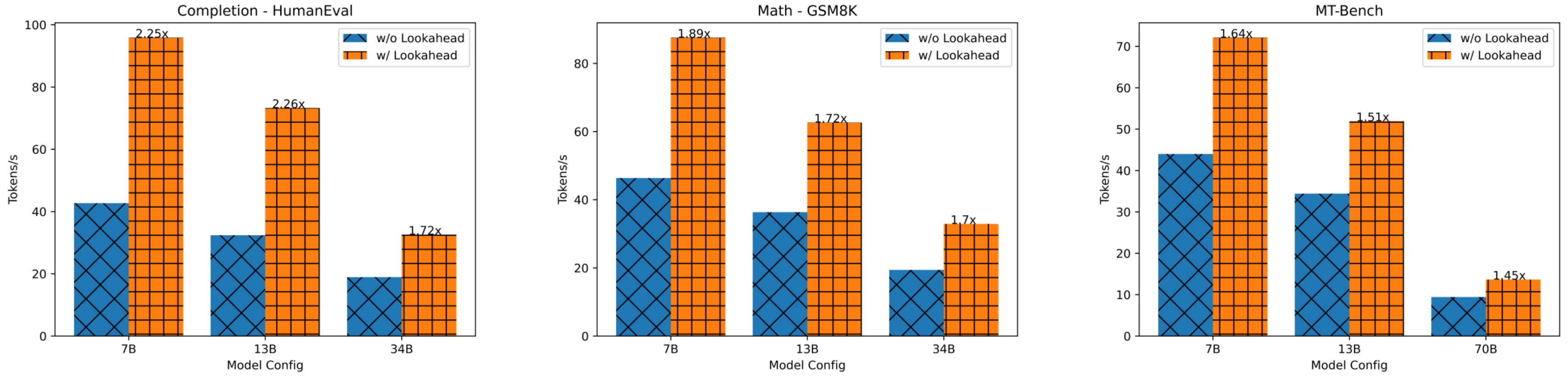
  • LLaMA-Chat on MT-Bench => 1.5x speedup

  • CodeLLaMA on HumanEval: 2x speedup. This is because many repeated N-grams are present in code which can be correctly guessed.

  • CodeLLaMA-Instruct on GSM8K: 1.8x latency reduction.