Resolving Interference When Merging Models
논문 정보
- Date: 2023-10-17
- Reviewer: hyowon Cho
- Property: Task Vectors
Introduction
각 태스크에 맞춰서 모델을 finetuning하는 것은 좋은 성능을 보장하나, 다음의 문제를 가진다.
-
새로운 application이 필요할 때마다 새로운 모델이 학습 및 저장되어야 함
-
단독으로 학습된 모델은 관련된 다른 태스크를 학습함으로써 얻을 수 있는 in-domain performance 상승효과 or out-of-domain generalization를 얻을 수 없다.
이를 방지하기 위해 Multitask learning이 흔히 사용되지만, 이 또한 다음의 문제를 가진다.
-
costly training and simultaneous access to all tasks.
-
또한, 모든 task에 도움이 되는 mix of datasets을 찾는 것은 복잡한 문제이다.
최근에는 이러한 문제점을 해결하기 위해 merging 도메인이 주목받고 있다. 대표적인 방법론들은 다음과 같다:
-
summing the individual model weights with different weighting schemes, either via a simple average
-
more sophisticated means that incorporate parameter importance
-
by task vectors
weighted averaging은 일정 수준 좋은 성능을 내고 있다는 사실을 입증했지만, 모든 언급한 방법론들은 업데이트되는 파라미터들이 내부적으로 방해가 되고, 이것이 모델의 성능 하락으로 이어질 가능성을 간과한다.
In this paper, we first demonstrate that interference can stem from two major causes:
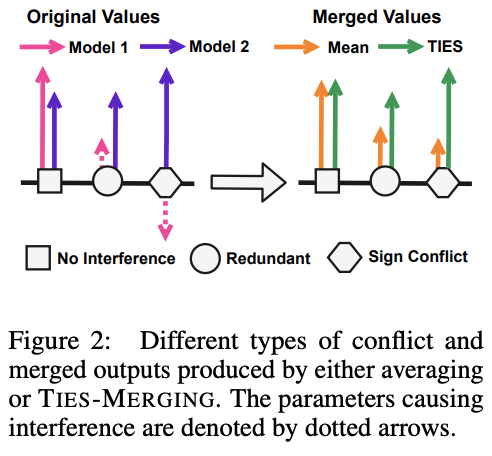
- INTERFERENCE FROM REDUNDANT PARAMETERS:
- model pruning과 관련된 기존 연구에서는 finetuning 과정에서 여러 모델 파라미터가 변경되지만 성능에는 미미한 영향을 끼칠 수 있다는 사실이 발견되었다. 하지만 한 모델에게 영향력을 미치는 파라미터가 다른 모델에게는 필요없어 불필요한 파라미터로 취급을 받을 시, 영향력있는 값이 가려져 전체 모델의 성능이 감소할 수 있다.
- INTERFERENCE FROM SIGN DISAGREEMENT
- 특정 파라미터는 어떤 모델에서는 양의 값을 가질 수 있고 다른 모델에서는 음의 값을 가질 수 있다. 따라서 간단한 평균을 취하는 것은 두 작업 모두에서 성능을 저해할 수 있다. 단순 평균은 Merged model에서 파라미터 값을 축소시키는 interference가 발생할 수 있기 때문이다. 영향력 있는 파라미터 간의 이러한 간섭이, 모델 merging과 멀티태스크 훈련 모델 간의 성능 차이가 모델 수가 증가함에 따라 증가하는 이유일 수 있다.
이러한 문제들을 해결하기 위해 저자들은 다음의 방법론을 제안한다: TIES-MERGING (TRIM, ELECT SIGN & MERGE). 이는 세 가지 스텝을 통해 만들어진 task vector를 이용하여 모델을 merging하는 방법론이다. 적혀 있듯이, 각 task vector에서 어떤 값을 trim할 지 정함으로써 redundant parameter 문제를 해결하고, 부호를 elect하여 sign conflict 문제를 해결하고, 마지막으로 merging을 시도한다.
저자들은 다양한 실험을 진행함으로써 해당 방법론이 효과적임을 입증한다.
-
different modalities, including language and vision benchmarks
-
distinct model sizes and families, such as T5-base and T5-large as well as ViT-B/32 and ViT-L/14
-
in-domain and out-of domain tasks,
-
full finetuning or parameter-efficient finetuning
결론적으로 Task Arithmetic, RegMean, Fisher Merging, and weight averaging과 같은 merging method들보다 훨씬 좋은 결과를 낸다는 사실을 확인했다. (하지만 multitask 만큼 도달하지는 못함!)
Background and Motivation
학습 방법: full finetuning or peft(IA3) Task vector = \theta{ft} - \theta{init}
Redundancies in Model Parameters
저자들이 먼저 강조하는 것은, 모델의 대부분의 파라미터들이 사실 태스크를 수행하는데에 redundant하다는 것이다.
다음의 그림은 11개의 task-specific task vector를 top-k의 largest magnitude value만 남기도록 trimming을 한 후, 그들의 평균 정확도를 보여준다.
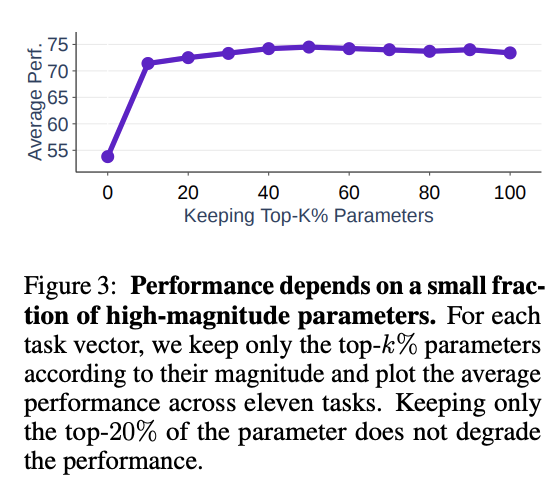
그림을 통해서 알 수 있듯, 전체 task vector의 20%만 남기는 것만으로도 전체 파라미터를 유지하는 것과 유사한 성능을 가지는 것을 확인할 수 있다. 즉, 이는 finetuning 과정에서 일어나는 대부분의 parameter change가 사실 상 redundant하다는 것을 의미한다.
따라서, 이러한 값들을 merging 시 무시하는 것은 task의 성능 저하에 크게 영향이 가지 않을 것이다.
Disagreement between Parameter Signs
각 finetuned model의 task vector는 각기 다른 부호를 가질 수 있다. 이는 merging시 interference를 일으킨다.
다음의 그림은 다양한 모델을들 merging할 시 일어나는 sign conflict의 빈도/퍼센트를 나타낸다. 해당 그림은 top-20%로 trimming을 시킨 후를 기준으로 한다.
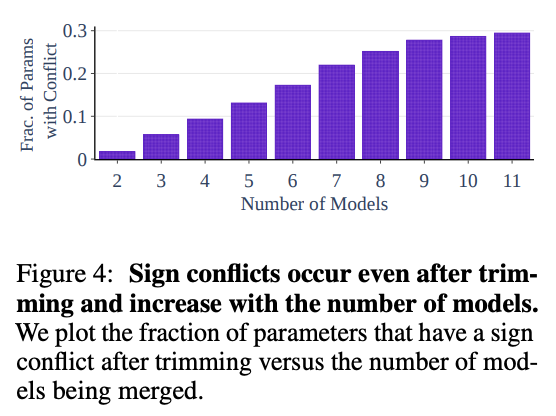
그림에서 볼 수 있듯, 단순히 두 개의 모델을 merging할 때도 sing conflict가 일어나며, 모델의 수가 늘어날수록 sign conflict가 일어날 가능성이 높아진다.
TIES-MERGING: TRIM, ELECT SIGN & MERGE
-
Notations:
-
\tau = task vector, == \gamma \odot \mu
-
\gamma = sign vector
-
\mu = magnitude vector
-
Steps in TIES-MERGING

-
Trim: keeping the top-k% values, reset others to 0
-
Elect: sign이 음수인 parameter는 그들대로, 양수인 parameter들을 그들대로 sum 구해서, 둘 중 더 큰 mass를 가지는 부호의 parameter들 만 남김
-
Disjoint Merge: 남겨진 param들의 mean을 취한다.
최종적인 모델은 \theta{init} + \lambda * \tau{m}이 되며 \lambda는 scaling hyperparamter.
Experimental Setup
-
Basslines
-
Simple Averaging: 전체 모델 파라미터 mean
-
Fisher Merging: 특정 task에 중요한 parameter를 찾기 위해 diagonal approximation of the Fisher Information Matrix Fˆt를 사용하는 방법론
-
RegMean: merged model과 individual model의 거리를 최소화시키면서 merging하는 방식
-
Task Artithmetic
-
individual fine-tuned models
-
multi-task model
-
Main Result
Merging PEFT Models
peft의 base model로는 t0-3b 사용함.
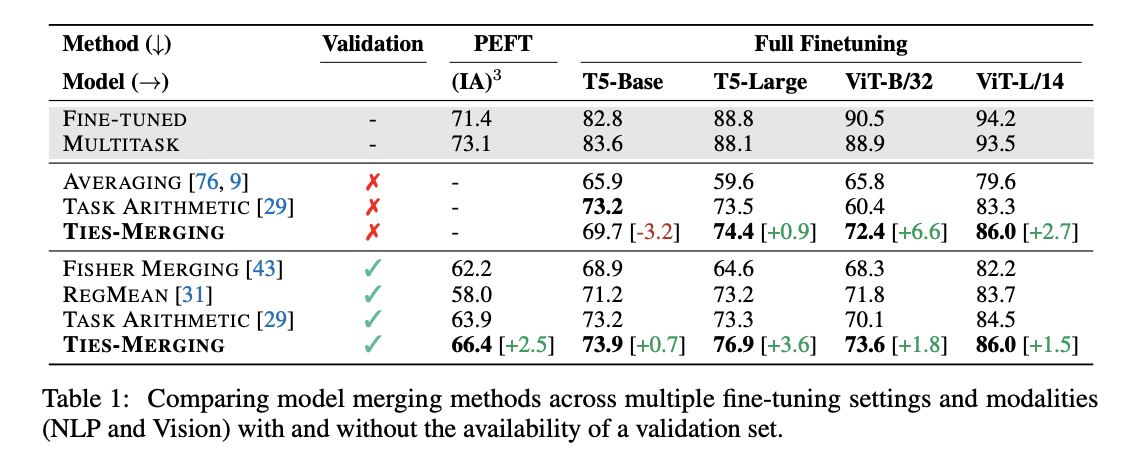
그림에서 볼 수 있듯, ties-merging을 할 시, 다른 거의 모든 merging 기법보다 좋은 성능을 보이는 것을 알 수 있다.
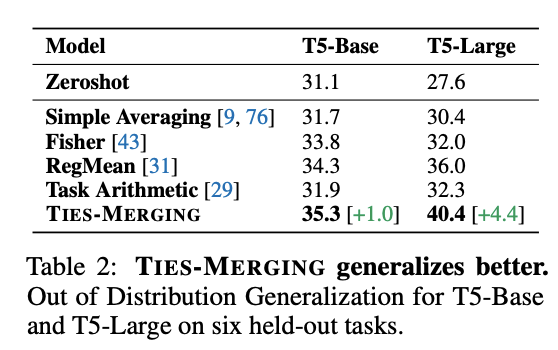
Out-of-Domain Generalization
대부분의 경우, multitask 모델은 학습에 사용되지 않은 다른 task에 더 빨리 domain shift가 일어나도록 하는 데 사용된다. 따라서, 이 실험에서는 7개의 task vector로 학습된 T5 모델을 6개의 다른 태스크에 적용해본다.
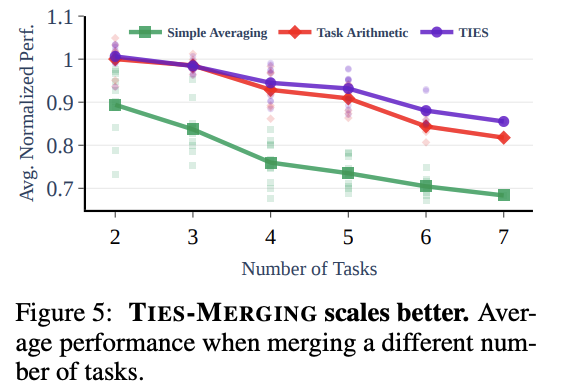
Merging Different Number of Tasks.
이번 실험에서는 task 개수가 늘어날 때의 영향력에 대해서 평가한다.
-
태스크 개수가 늘어나면 모든 method의 performance 감소
-
두 개의 태스크를 merging할 때, ties-merging과 task arithmetic의 성능 차이 미미
-
하지만 개수가 늘어날 수록 성능 차이 확실
Additional Results and Analysis
Types of Interference and Their Effect on Merging
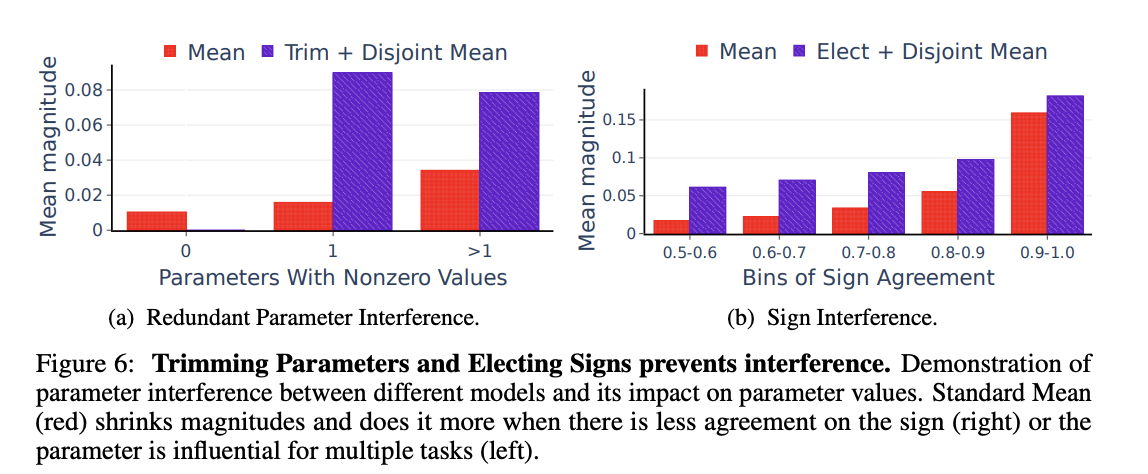
(a) Importance of Removing Redundant Parameters.
redundant parameter의 영향력을 실험하기 위해, 파라미터를 세 개의 그룹으로 나눈다
-
redundant parameters (using a trimming threshold of 20%)
-
parameters that are influential to exactly one model
-
parameters that are influential to more than one model
다음으로 두 가지를 비교한다: directly merged vs when they are first trimmed and then (disjointly) merged without electing signs.
(a) figure를 통해서 알 수 있듯, 단순 merging을 시킬 경우 어떤 특정한 task에만 중요한 vector의 중요도가 크게 감소하는 것을 볼 수 있다. 하지만 ties-merging을 통해서는 이것이 유지된다. 또한, 여러 개의 모델이 중요하다고 여긴 경우에도, 이러한 양상이 유지되는 것을 확인할 수 있다.
(b) Importance of Resolving Sign Interference.
Sign Interference의 영향력을 확인하기 위해, 파라미터를 그들의 부호에 따라 그룹화한다. 0.5는 서로 다른 모델 간의 특정 파라미터의 양의 부호와 음의 부로가 동일한 개수임을 나타내고, 1은 모든 매개변수가 동일한 부호를 가진다는 것을 의미한다. 비교하는 것은 두 가지, 부호 불일치가 해결된 후 병합되는 것과 단순 병합되는 것의 차이이다.
(b)를 통해서 확인할 수 있듯, ties-merging을 통해 부호 불일치를 해결했을 때, magnitude를 보존함을 보인다.
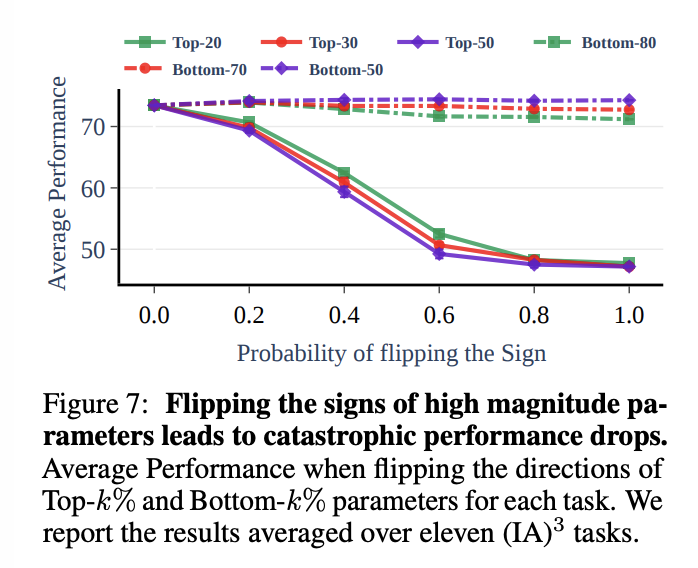
Relevance of Signs of the Top-k% Parameters
해당 실험에서는 IA3에서 top-k parameter와 그들의 direction이 task performance에 어떠한 영향을 끼치는지 정량화한다. 각 task vector에서 top-k parameter를 뽑아내고 그들의 sign을 반대로 적용한다. 그리고 이 task vector를 이용해 모델을 만들어 실험을 진행한다. Baseline으로 (100-k)% parameter를 뒤집어 만든 task vector model도 함께 report 한다.
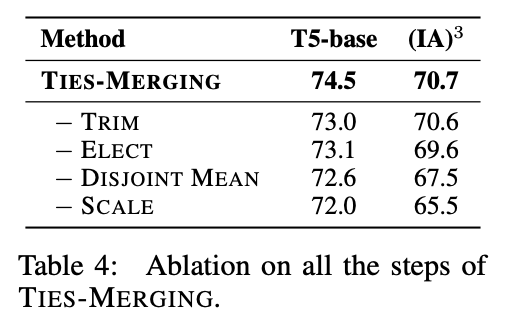
Ablation of TIES-MERGING Components
각 프로세스애 따른 성능 변화. 모든 과정이 중요했음을 강조한다
Importance of Estimating Correct Signs When Merging Models
부호의 중요성을 더 확인해보기 위해, 저자들은 multitask model을 만들어 task vector를 만들고, 이의 sign을 추출한다. 그 뒤, trim 과정을 통해 만들어진 vector에 해당 sign을 이용하여 elect&mean 을 수행한다.

결과는 놀랍다. 거의 multittask model에 준하는 결과를 얻을 수 있었다. 이것은 모델의 수정 방향만 얻을 수만 있다면 더 좋은 결과로 이어질 수 있다는 것이다.