Does Fine-Tuning LLMs on New Knowledge Encourage Hallucinations?

Created on June 11, 2024

2024   ·   alignment   fine-tuning   knowledge   language-model   llm   paper-review   pre-training   rlhf   ·   paper-reviews

논문 정보

  • Date: 2024-06-11
  • Reviewer: 준원 장
  • Property: LLM, Knowledge

1. Introduction

  • Large Language Model Pretraining

    • pre-training: parameter에 factual knowledge를 넣기

    • supervised fine-tuning: instruction following task에 sft해서 model에 alignment behavior 부여

    • rlhf: model에 preference behavior 부여

  • SFT stage에서 human annotator에 의해서 model이 alignment를 배우기도 하는데, pre-training때 학습하지 않는 지식을 대답하도록 annotating이 될 수 있다.

  • 여기서 해당 논문의 RQ가 등장.

⇒ (1) 과연 모델이 이미 존재하지 않은 지식을 (2) (supervised) fine-tuning으로 학습할 경우 기존 모델이 가지고 있는 지식체계에 어떤 변화가 생길까?를 굉장히 체계적으로 분석한 논문.

⇒ 이를 위해서 single fine-tuning example을 model의 knowledge에 따라서 총 4단계로 분류하는 카테고리 체계를 제시.

⇒ Model의 Knowledge를 평가하기 위해서, 또 controlled experiment setting을 구축하기 위해서 EntityQuestion(QA dataset)을 활용한 것은 분명한 한계가 있지만, 역설적으로 가장 통제적인 실험을 하기 위한 세팅이 아니었나라는 생각.

  • 논문의 결론

⇒ LM이 Unknown fine-tuning example을 학습하는것도 pre-existing example에 대한 hallucination은 linear한 correlation 관계가 있다.

⇒ Unknown Example이 Known Example에 비해서 fitting되는데 시간이 오래걸리며, Unknown Example에 의한 hallucination을 제거하기 위해서 Early Stopping이 필요함을 실험적으로 계속해서 보임.

⇒ Known Example로 그 카테로리를 fine-grained하게 나눠서 LM에 미치는 효과를 분석.

⇒ LM은 대부분의 지식을 pre-training stage에서 배운다. Fine-tuning에서 새로운 지식을 학습시키면 결국 배우긴 하지만 pre-training stage에서 학습한 지식의 hallucination을 발생시킨다.

⇒ Fine-tuning은 pre-training때 학습한 지식을 활용하도록 mechanism을 설계해야 한다.

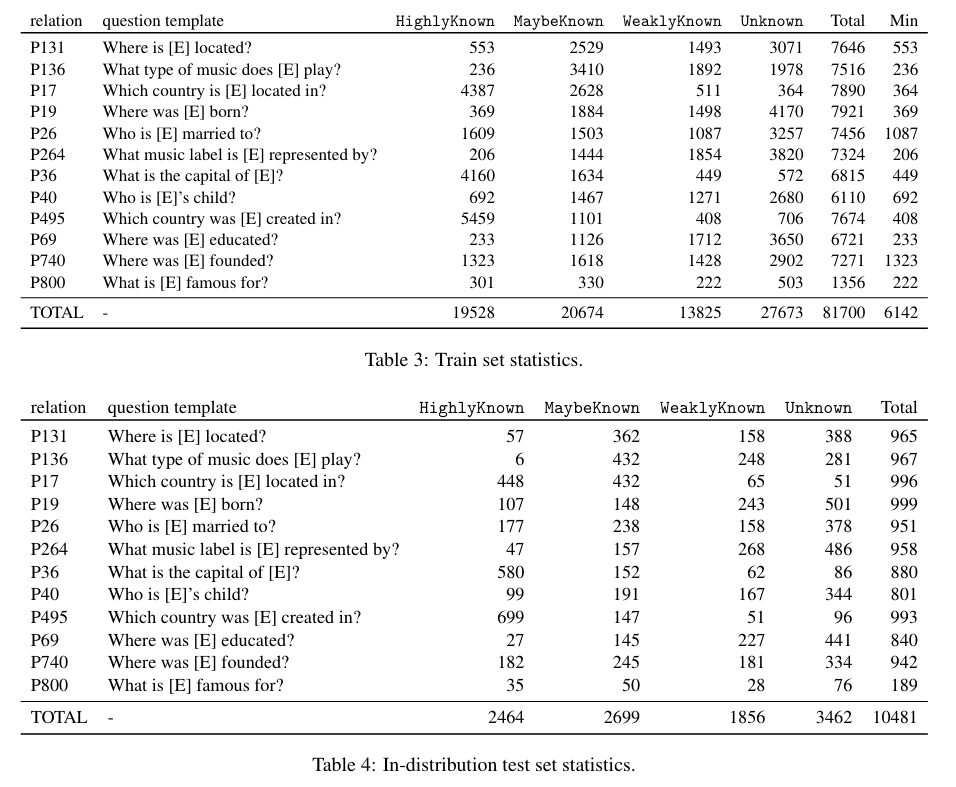
2. Study Setup

  • Fine-tuning dataset : D

    • ENTITYQUESTION (subject, relation, object)

    • q: Where is Paris located?

    • a: France

→ 12 relations를 LM에 태워서 UNK, KN sample (i.e., train sample)로 분리

→ (OOD) 7 relations를 LM에 태워서 UNK, KN sample (i.e., test sample)로 분리

  • Training Pipeline

    • M \rightarrow D={(q{i},a{i})}{i=1}^{N} \rightarrow M{D}

  • Model

    • PALM2-M

  • Metric

    • EM

3. Quantifying Knowledge in LLMs

  • D={(q{i},a{i})}_{i=1}^{N}에 있는 데이터가 M이 알고 있는지 아닌지 판단하는 과정

SLICK

⇒ M이 q를 집어 넣었을때 a를 잘 대답하는가?

  1. q와 유사한 (relation이 같은) few-shot exampler 4개 sampling

  2. temperature T 설정.

  3. 모델이 a를 제대로 맞출 확률 P_{correct}(q,a;M;T) estimate

  4. 각 example에 대해서 N_{ex}=10번씩 estimate.

  5. P_{correct}(q,a;M;T=0)

  6. greedy answer

  7. P_{correct}(q,a;M;T=0.5)

  8. highly logit에 더 높은 확률 주게 resampling

  9. Top 40에서 N_{sample}=16개를 sampling

  10. M \rightarrow D={(q{i},a{i})}{i=1}^{N} \rightarrow M{D}

⇒ P_{correct}(q,a;M;T) 로 knowledge 카테고리 분류

  • LM이 한번이라도 맞추면 Known, 아니면 Unknown으로 분류.

  • 여로 demonstration에 대해서 Greedy Decoding과 temperature sampling에 대해서 생성된 answer들을 가지고 Known 카테고리를 세분화

4. How Harmful are Unknown Examples?

  • D 를 고정하고 Unknown Example의 비율을 바꿔가면서 LM을 training해가면서 변화추이를 관측

  • Known Example은 일단 collectively하게 측정.

    • 이후에 ablation으로 fine-grained하게 측정.

⇒ Disjoint Test를 hallucination 척도로 활용

  • Disjoint setting이기 때문에 Test set에는 2개 type question이 존재

  1. UNK Question → 어떤 trainset으로 학습해도 모델이 맞추질 못함

  2. KNOWN Question → Training set 이후 모델이 맞추는지 확인이 가능함

⇒ Dev에서 수렴하면 Early Stopping

⇒ Training Dataset Acc 100% 달성하면 Early Stopping

#### Higher Unknown Ratio is Proportional to Performance Degradation

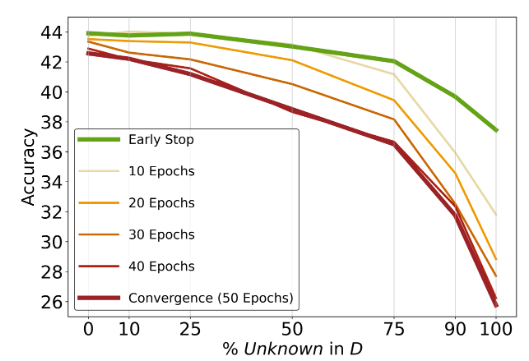
  • Unknown비율이 많을수록 성능이 악화됨 (training duration 상관 없이 같은 경향)

  • Unknown 비율이 높을때, Early Stopping이 risk of overfitting에 도움이 됨

#### Unknown Examples: Harmful or Neutral?

  • 위의 실험에서는 (1) Unknown example이 정말 LM의 parametric knowledge와 discrepancy가 커서 performance degradation이 일어나는지 (2) Known example 수가 줄어듦에 따라 Neutral한 효과를 주는것인지 불분명

  • D 에서 Unknown Example만 따로 빼서 D_{known} 구축 후 fine-tuning, 실험결과 추가로 plotting

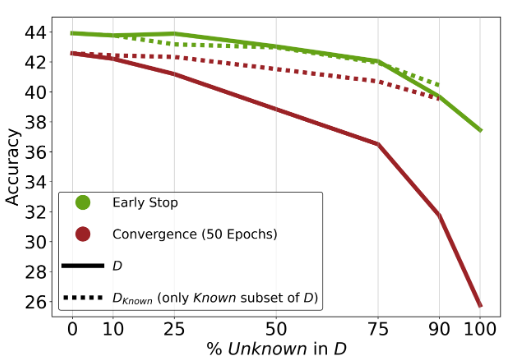
  • Early Stop을 할 경우 Unknown Example은 neutral한 효과를 가짐.

  • Convergence할 경우 Unknown Example은 harmful한 효과를 가져옴

  • Early Stop ↔ Convergence의 gap이 D_{known}보다 D에서 더 큰데, 이를 통해 Unknown sample이 overfitting에 취약함을 알 수 있다.

#### Unknown Examples are Fitted Slower than Known Examples

  • Early Stopping이 Unknown example이 later training stage에 fitting되어서 negative 영향을 미치는 것을 보았는데, training dynamics 분석을 통해 어떤 sampling이 fine-tuning stage에서 빠르게 fitting되는지 보다 명시적으로 분석함.

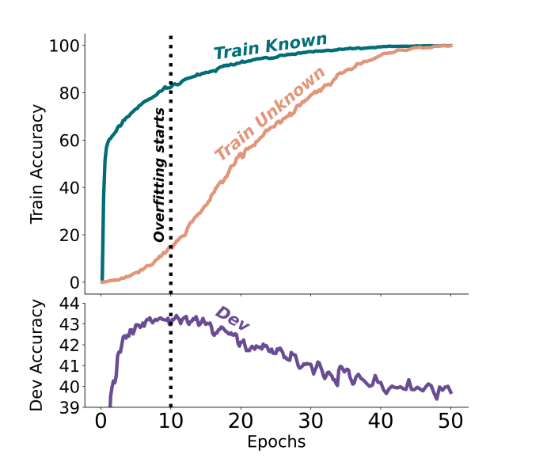
  • (UNK 50% vs KNOWN 50%) Known Samples가 Unknown Samples보다 훨씬 더 빠르게 fitting되고 Early Stop으로 끊는 위치에서 Training Known의 fitting 비율이 압도적으로 높은 것을 확인할 수 있다.

  • Known 카테고리를 변경해가면서 Early Stop 직후 Training sample 내 UNK vs KNOWN이 얼만큼 fitting 되어있냐를 확인해보면 (아래그림) Known이 압도적인 비율임을 확인함을 볼 수 있으며, 이전 Early Stoping의 Neutral Effect에 대한 해석을 제시함

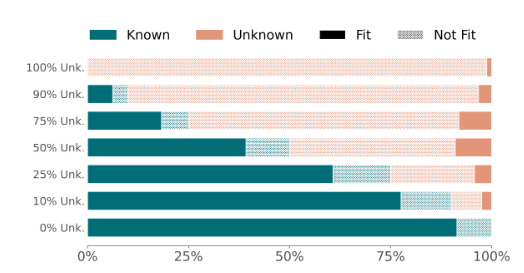
#### The Influence of Unknown vs Known on Accuracy: A Linear Model Perspective

  • Known Example과 Unknown Example 개수를 Test Acc와 linear 관계로 표현

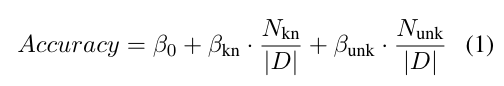
  • Unknown examples은 음수(hurts performance), Known examples는 양수(improves).

  • Test samples가 OOD(이 setting에서는 relation이 다름)이라도 경향성은 같음

  • In-Distribution

  • Out-of-Distribution
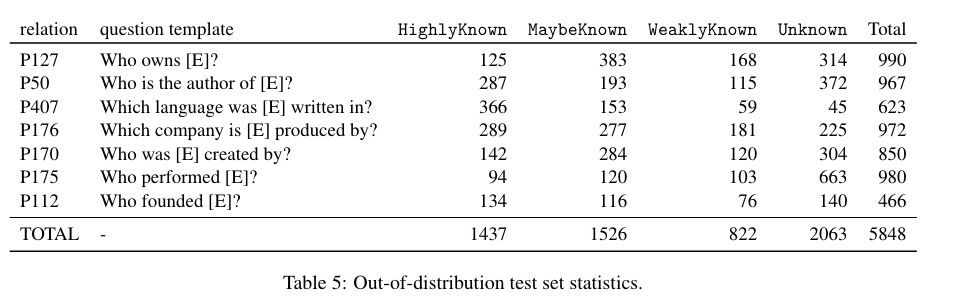
  • “Where is [E1] located?”라는 데이터로 convergence 시키면 “Who founded [E2]?”라는 질문에 hallucination을 일으킬 수 있음.

5. Understanding Knowledge Types: Their Value and Impact

  • 지금까지 진행했던 실험에 대해서 조금 더 fine-grained된 실험을 진행

  1. 각 training sample의 knowledge 카테고리가 test performance에 어떻게 영향을 미치는가?

  2. 2.에서 구축한 카테고리 별로 나눠서 gap이 D_{CAT}

  3. ENTITYQUESTION의 natural distribution 따르는 D_{natural}

  4. 각 test examples 카테고리별로 다를까?

  5. test example도 2.처럼 분류함

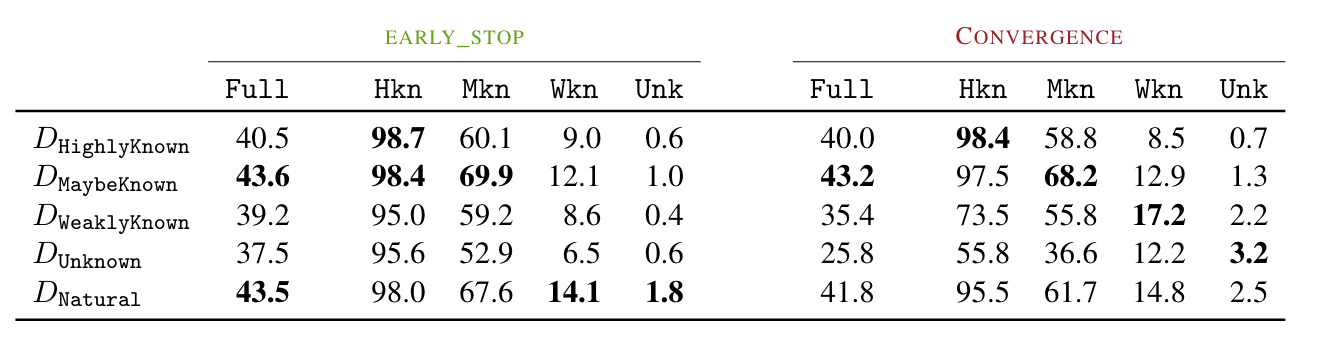
  • Highlyknown으로만 학습하는게 가장 좋을것 같지만, Highlyknown한 disjoint test에서만 가장 성능이 좋다.

  • 의외로 Maybeknown이라고 판정받은 training dataset으로 학습하는게 (Highly, Maybe) 전반적으로 가장 성능이 좋다.

  • Weakly Known과 Unknown으로만 학습할 경우 Early → Convergence로 갈 시 각각의 카테고리에서 큰 개선이 있지 않는것 대비 (8.6%→ 17.2% & 0.6% → 3.2%) Highlyknown과 Maybeknown처럼 이미 알고 있는 지식체계가 많이 파괴되는 것을 알 수 있다.

(Unknown으로 학습후도 disjoint test set의 Unknown이 낮아야 disjoint test에 대한 실험 타당성을 이야기할 수 있는데 장표를 보면 낮음(3.2%)

  • 같은 이야기지만 D{natural}이 D{maybeknown}에 비해서 EarlyStop 이후에 수직낙하하는 것을 D{natural}에 Weakly Known과 Unknown되어 있기 때문이라고 설명하며, D{maybeknown}이 overfitting 방지와 top performance에 좋다고 이야기함.

6. Conclusion

  • superficial hypothesis에 따르면 LLM이 지식을 pre-training때 학습하고 SFT는 단순 alignment를 학습한다고 주장 (LIMA).

  • 여기에 더해 LM이 UNK Example에 대해서 학습하기 어렵다는 것, Highlyknown을 추가적으로 학습하는게 suboptimal utilization으로 어이진다는 밝혀냄으로, superficial hypothesis에 힘을 실어 SFT 데이터를 구축할때 LM의 pre-existing KG를 고려할 것을 강조.