Stacking Your Transformers: A Closer Look at Model Growth for Efficient LLM Pre-Training
논문 정보
- Date: 2024-06-04
- Reviewer: 김재희
- Property: LLM, Pre-Training
1. Intro
-
TL;DR
-
큰 모델의 initial weight로 작은 모델의 weight를 stacking하는 것이 효과적
-
동일 자원 하에서 random init보다 더 빠르게 높은 성능 달성 가능
-
다양한 expansion 기법 중 vertical stacking이 가장 효과적
-
scaling law 관점에서 stacking timing도 함께 실험하여 제시
-
-
Related Works
-
Model Expansion: 학습된 모델에 대해 weight를 확장하여 성능 개선을 목표
-
BERT scale에서 pretrain 시 model expansion에 대한 연구들 존재
-
BERT Stack,
- 학습된 bert layer를 통으로 vertical하게 쌓는 방식 제안
-
-
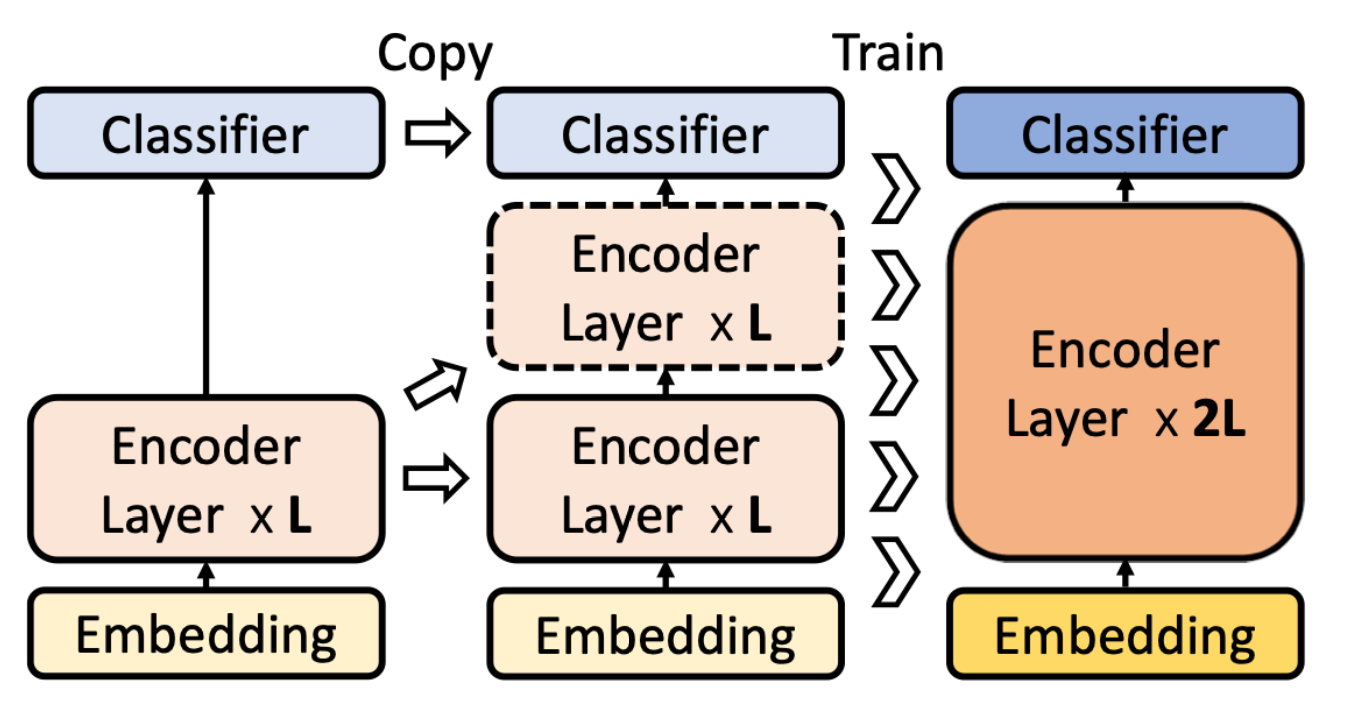
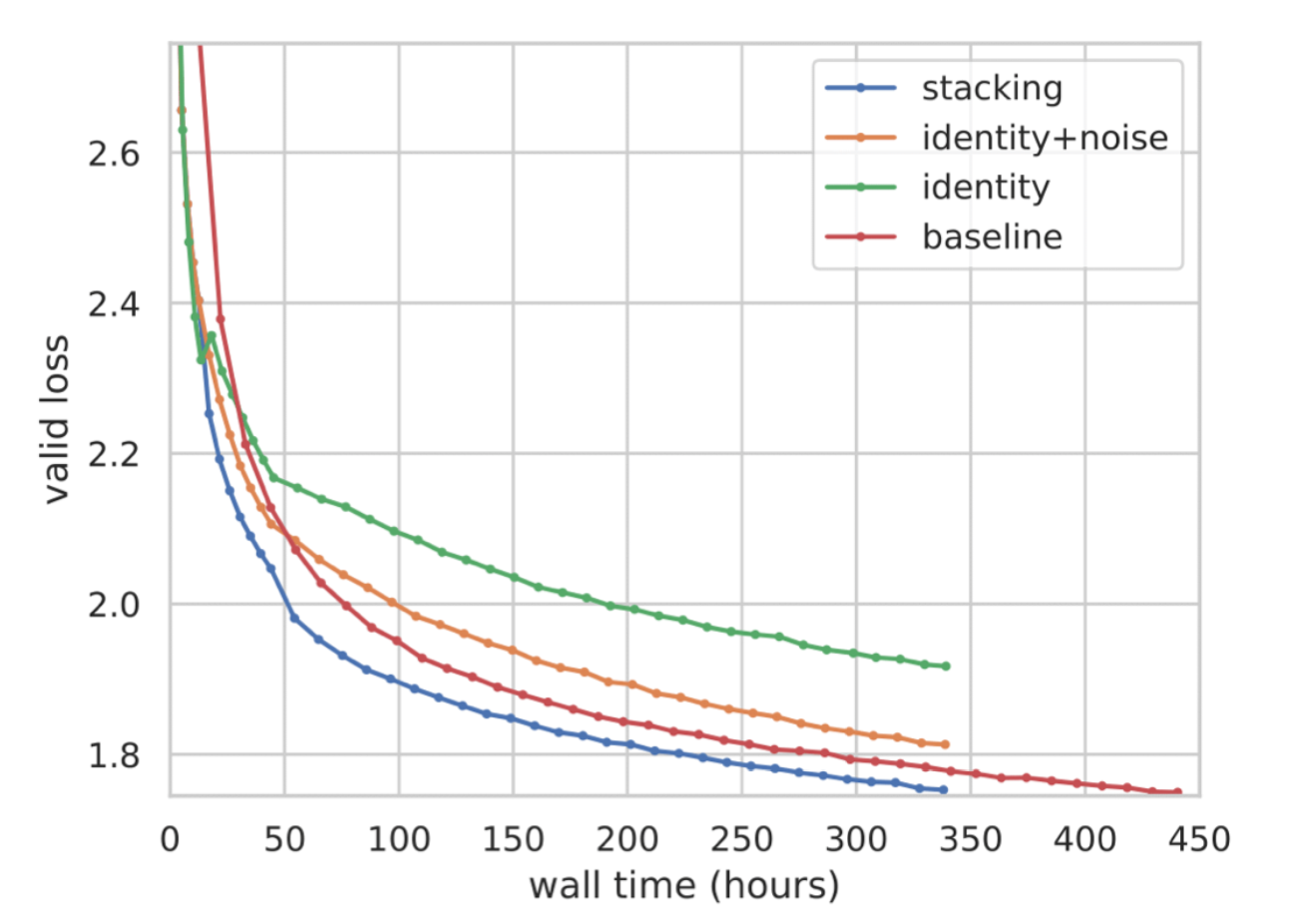
- 다양한 weight init 방식보다 효과적
- Progressive Stacking 2.0
- 모델의 초기 레이어부터 하나씩 학습시키면서 stacking
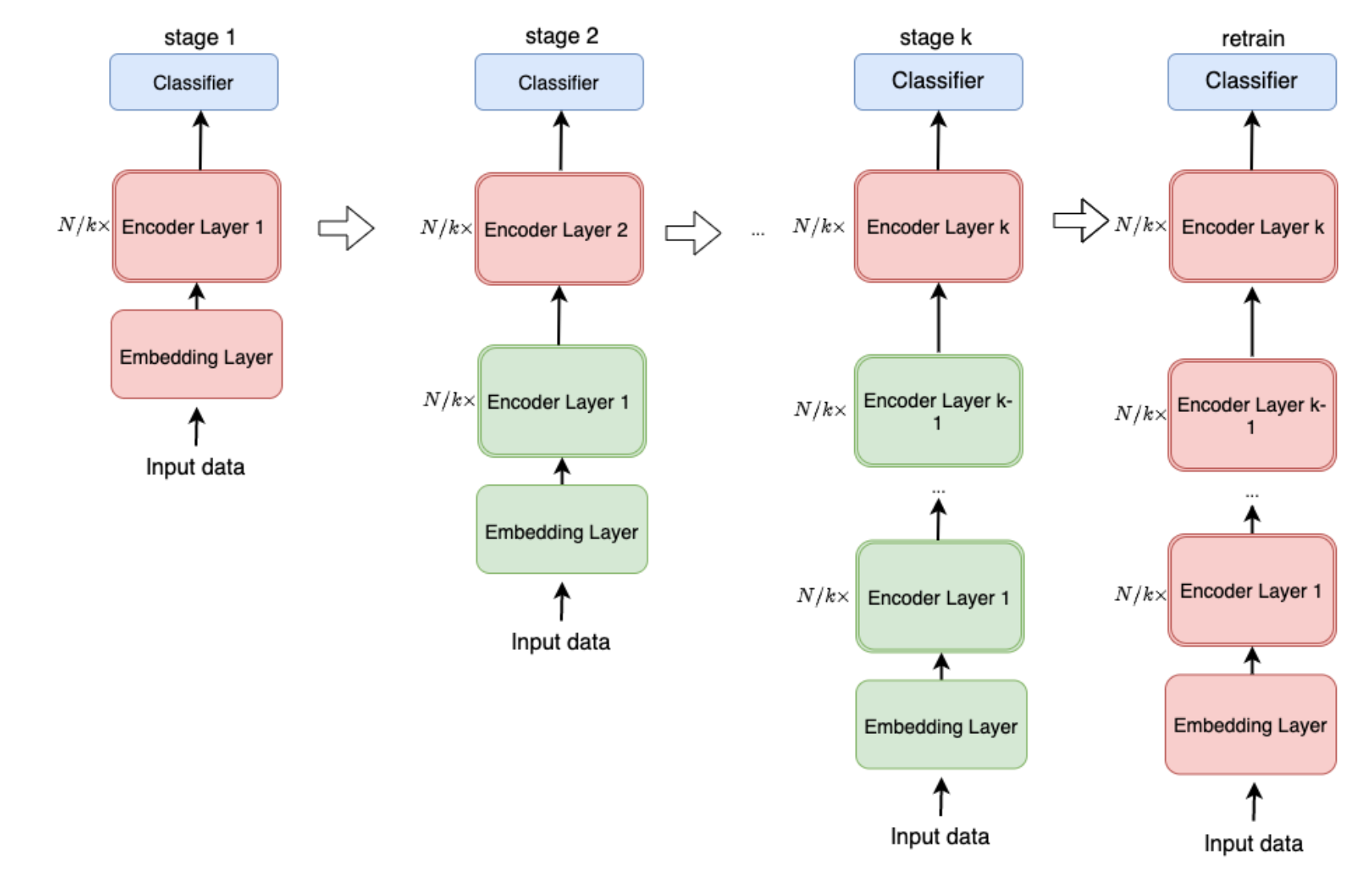
- 모든 레이어를 한번에 학습하는 것보다 1회 iteration이 빨라지게 됨
- 초기에는 적은 레이어만 forward/backward에 사용되니까

- LiGO
- 학습된 초기 모델의 weight를 이용하여 vertical, horizontal expansion 방법론 제시
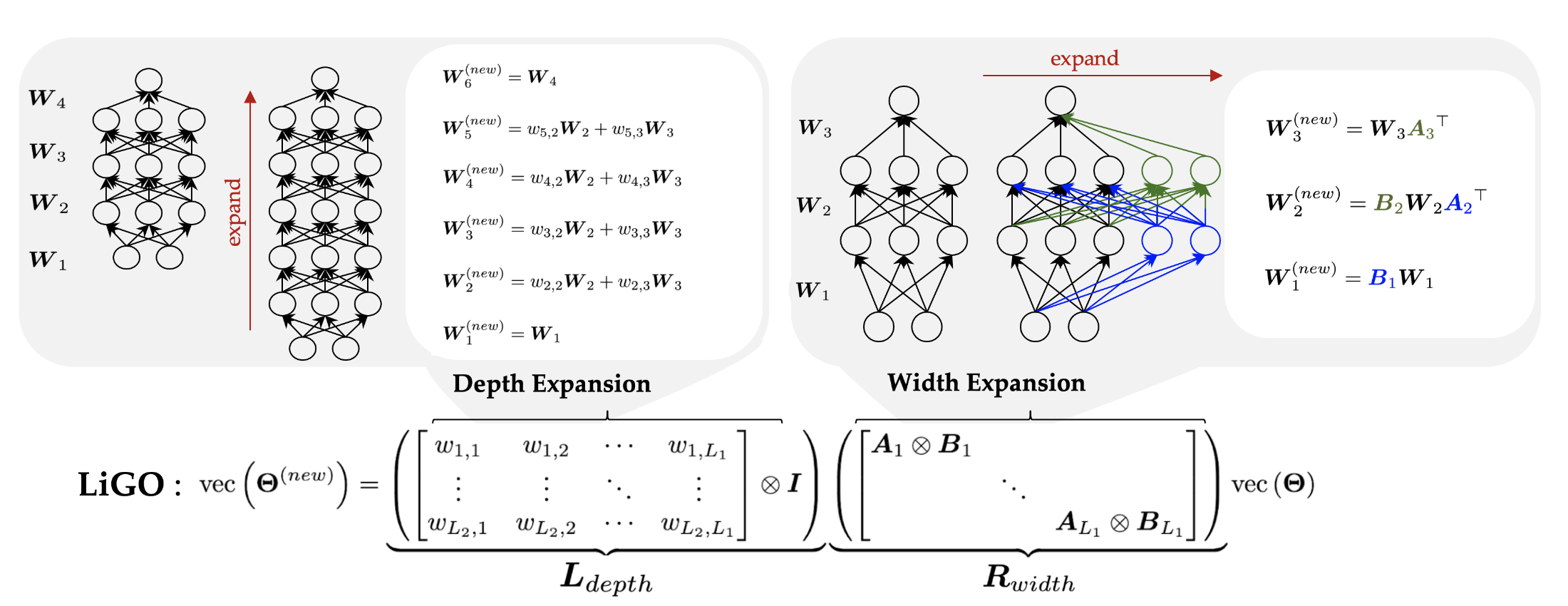
- 새로운 weight: 기존 weight의 knowledge를 보존할 수 있는 분해 방법론 사용
- 큰 모델을 한번에 from scratch로 학습하는 것보다 빠른 시간 내 학습
- 성능 개선 X, 학습 효율화

2. Expansion Method 비교 실험
Expansion methods
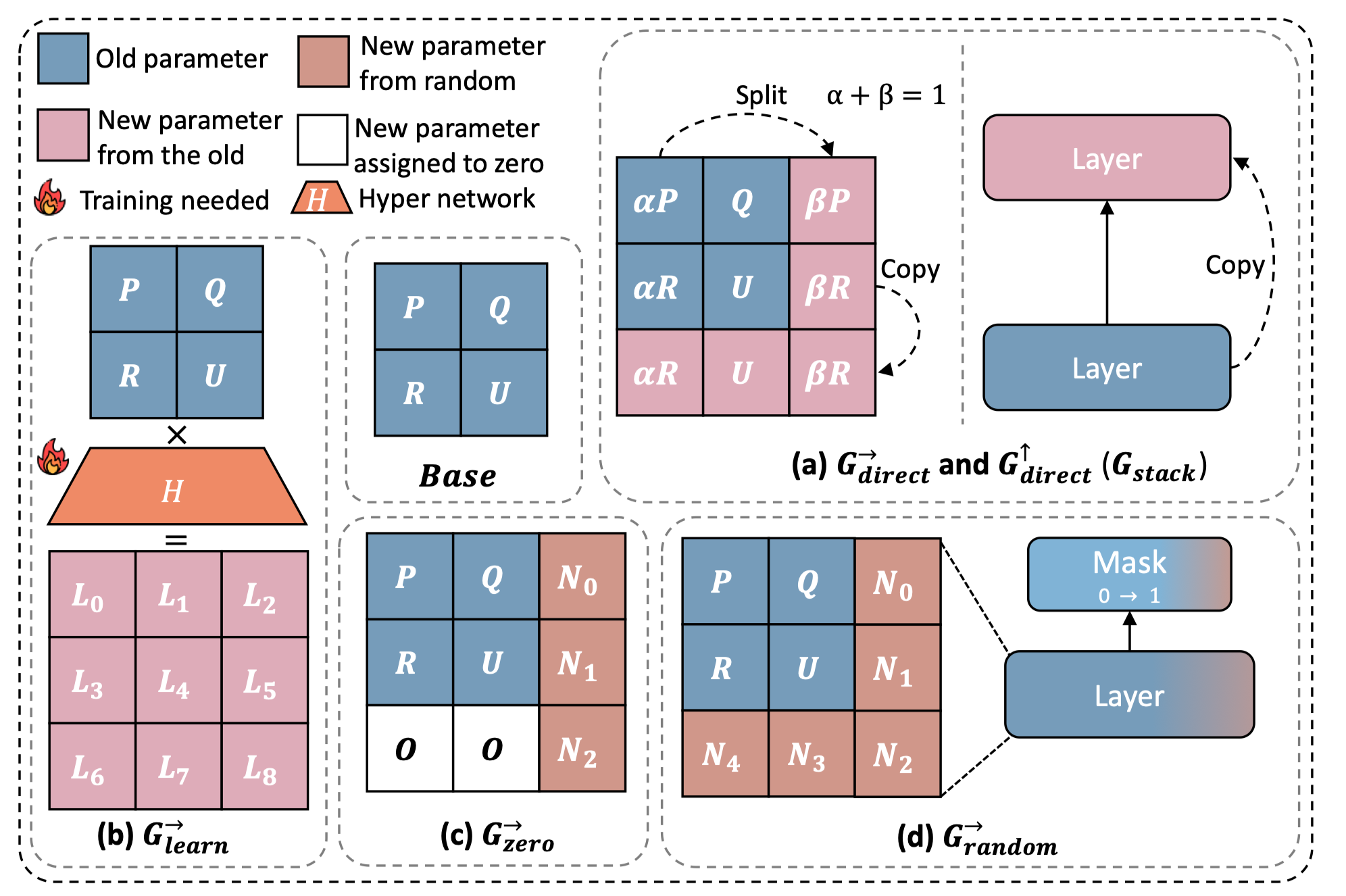
-
총 4가지 파라미터 확장 방법론을 실험 대상으로 선정, dimension: (in, out)
- 적용 layer: MLP, Multihead Attention
-
vertical stacking: 학습된 작은 모델의 weight를 복사하여 초기값으로 활용
-
G_stack: 새롭게 만드는 상위 레이어 파라미터를 작은 모델의 weight를 복사하여 사용
-
G_direct(→): 기존 레이어의 weight를 분할하여 새로운 weight의 초기값으로 활용
-
learnable expansion(G_learn): 학습된 작은 모델의 weight matrix에 대한 learnable parameter를 도입하여 확장된 weight matrix를 학습하는 방법론
-
zero init(G_zero): weight matrix의 파라미터 확장 시 random과 init을 함께 활용하는 방법론
-
random init(G_random): weight matrix의 파라미터 확장 시 모든 weight를 random으로 init하는 방법론
ffnn layer
-
(d_model, d_model*4)
-
relu
-
(d_model*4, d_model)
Training Small Model
- 초기 모델 학습 → expansion method를 적용하여 larger model 추가학습 진행
→ 동일한 초기 모델을 이용해서 큰 모델 초기값을 설정할 때, 적절한 expansion 전략 탐색 목적
-
초기 모델 크기: 400M
-
학습 데이터수: 10B token
-
400M → Expansion Method → 1.1B (107.5B token)
-
larger model 학습
-
모델 크기: 1.1B
-
97.5B token
-
-
from scracth 모델 학습
-
1.1B 모델을 scracth부터 학습 진행
-
baseline으로 사용
-
100B 토큰 학습 → 초기모델 + larger 모델과 동일한 연산량 학습
-
실험 결과
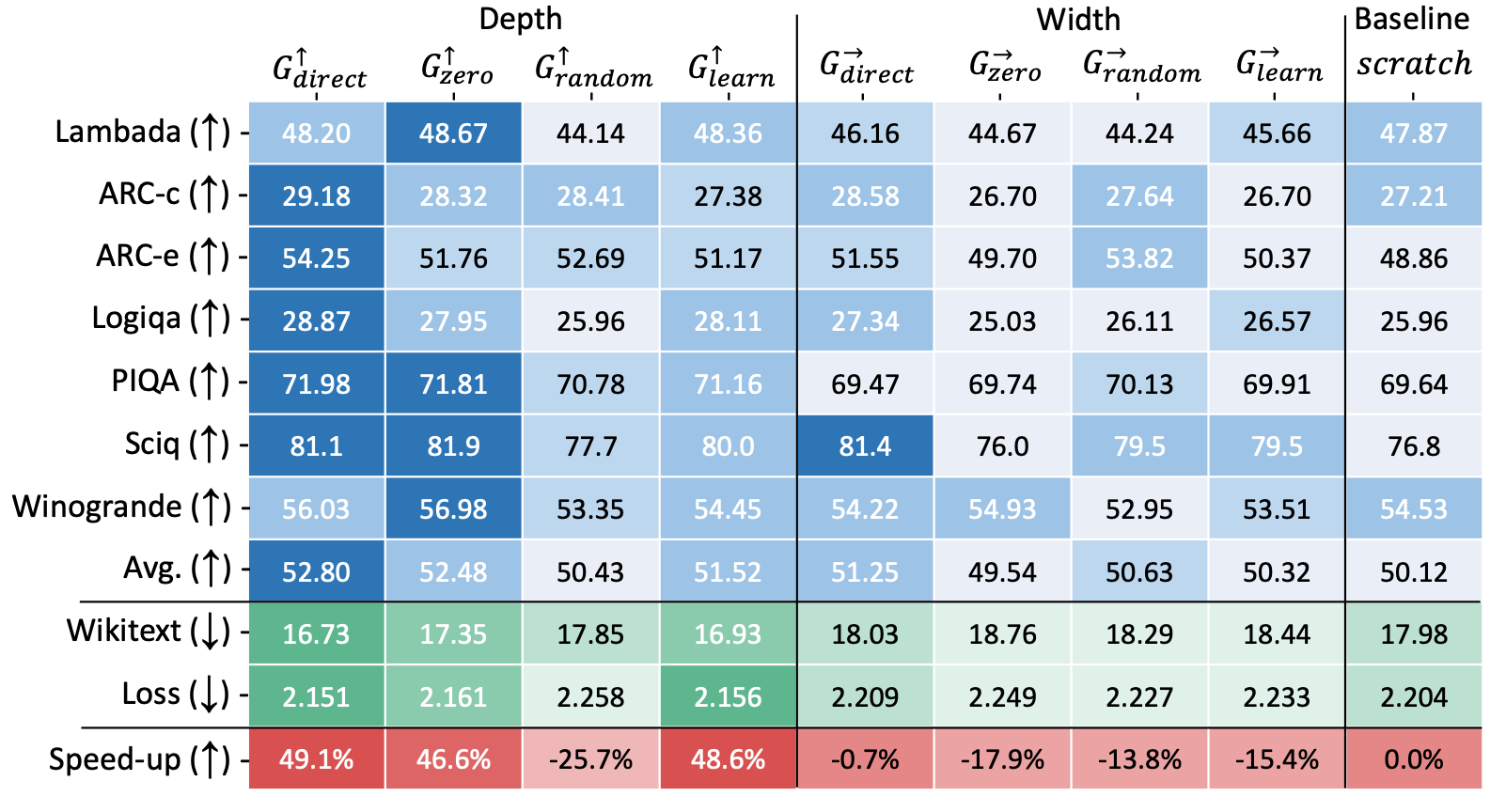
-
speed-up: scratch 모델과 동일 성능 도달을 위해 필요한 연산량(FLOPS)
-
양수: 해당 비율만큼 scratch모델보다 빠르게 성능 도달
-
음수: 해당 비율만큼 느리게 성능 도달
-
-
G_direct(up): 학습 속도 및 성능 측면 모두에서 타 방법론 및 scratch 성능 능가
-
거의 모든 지표에서 타 방법론 대비 높은 성능 달성
-
모든 지표에서 scratch 모델 대비 높은 성능 달성
-
-
vertical stacking 방법론이 horizontal stacking 방법론보다 높은 성능 달성
-
vertical stacking 시 zero가 random보다 높은 성능 달성
-
(재희): 기존 모델이 생성하는 representation에 대해 변화를 가하는 레이어를 추가했기 때문
-
random: noise에서 시작하여 의미있는 변화를 주는 방향으로 학습해야 함
-
zero: 변화를 주지 않는 것에서 시작하여 변화를 주는 방향으로 학습해야 함 → 훨씬 쉬움
-
-
3. Delving Deeper Into Vertical Stacking
growth factor(g)
-
기본 모델 M이 주어져 있을 때, stacking 횟수 인자
-
Vertical Stacking이 가장 성능이 좋은 것으로 나타났음
→ stacking 횟수 및 시점이 중요한 문제가 될 것
Scaling Model Size
-
3B와 7B larger model을 타겟으로 실험 진행
-
각각 (0.75B, 1.75B)를 가지는 기본 모델 훈련 진행 (w/ 10B token)
- 학습된 기본 모델을 4번 Stacking하여 300B token에 대한 추가학습을 진행
실험 결과
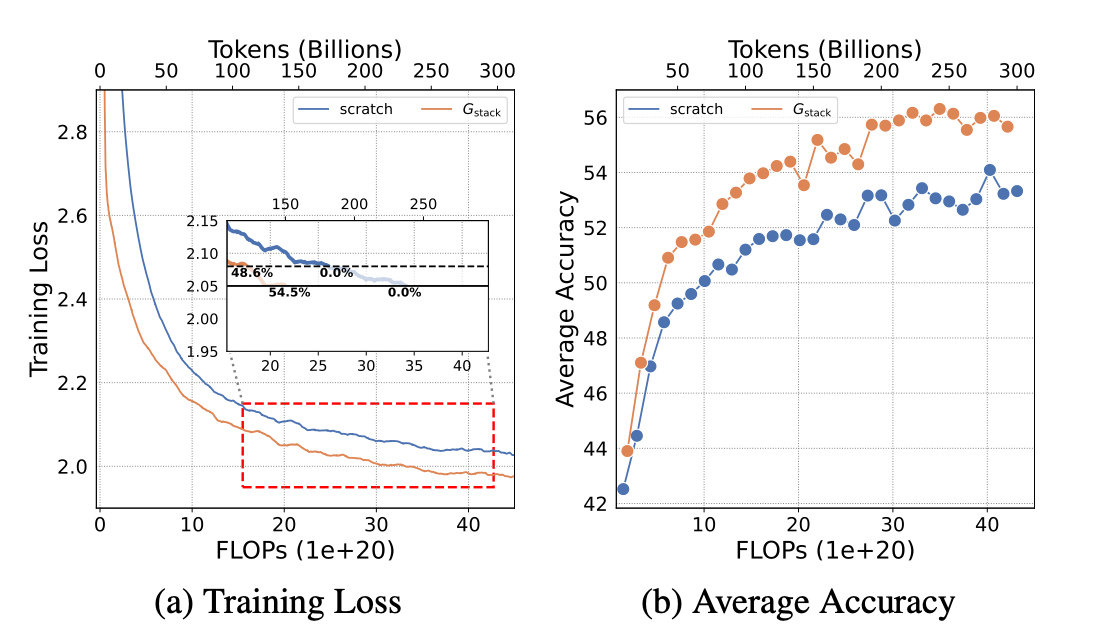
-
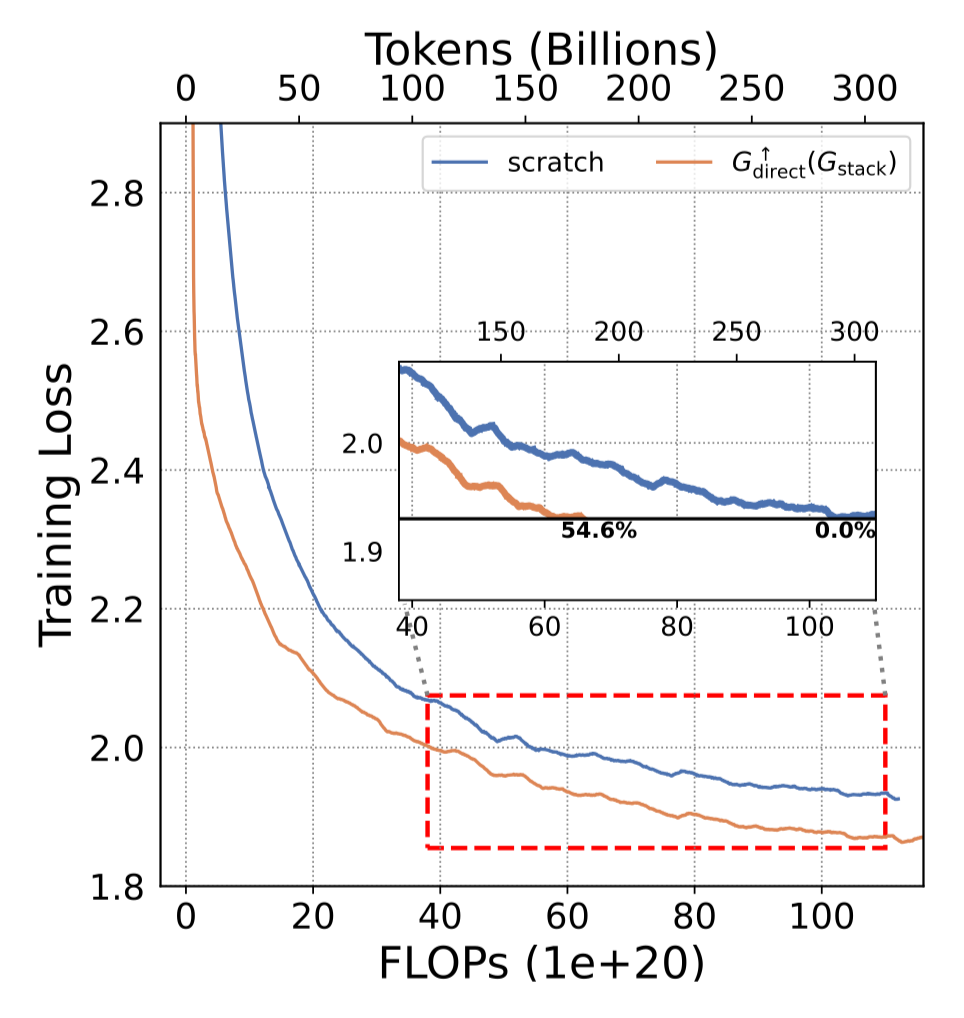
3B
-
성능도 더 빠르게 수렴하고, loss도 더 빨리 떨어지는 모습 + saturation되지 않음
-
Chinchilla Scaling Law 이상으로 학습했는데도 scratch 모델과 유의미한 차이가 발생 + 간격이 벌어지는 현상 관찰
-
scratch 모델과 동일 성능 도달을 위해 54.5%의 연산량 절감 가능
-
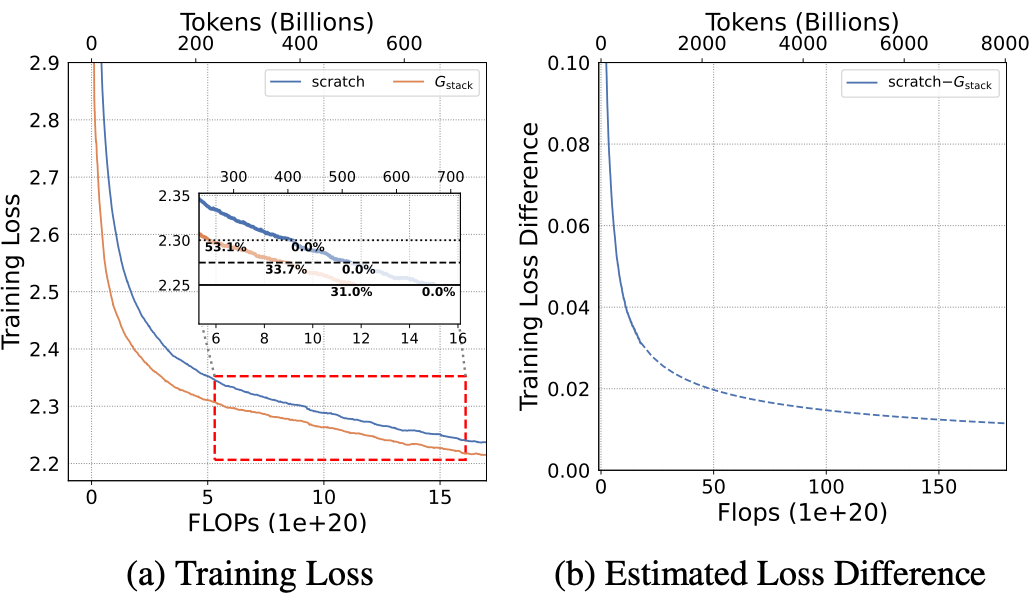
Longer Train vs Scaling Effect
- Stack의 효과가 아니라, 단순하게 token을 더 많이 써서 학습해서 성능이 오른 것일수도 있음
-
400M 모델을 이용하여 410M vs 840M(410M 모델 stacking) 모델 간의 성능 차이 관찰
-
꾸준한 성능 차이 관찰
-
학습이 지속되면서 성능 격차가 줄어드는 모습 관찰 가능
-
Scaling Law가 존재하지 않을까?
-
Base Model의 크기, Larger Model의 크기 Stacking 시점에 따른 최적의 조합 탐색 필요성 존재
-
4. Scaling Law
Toy Plotting
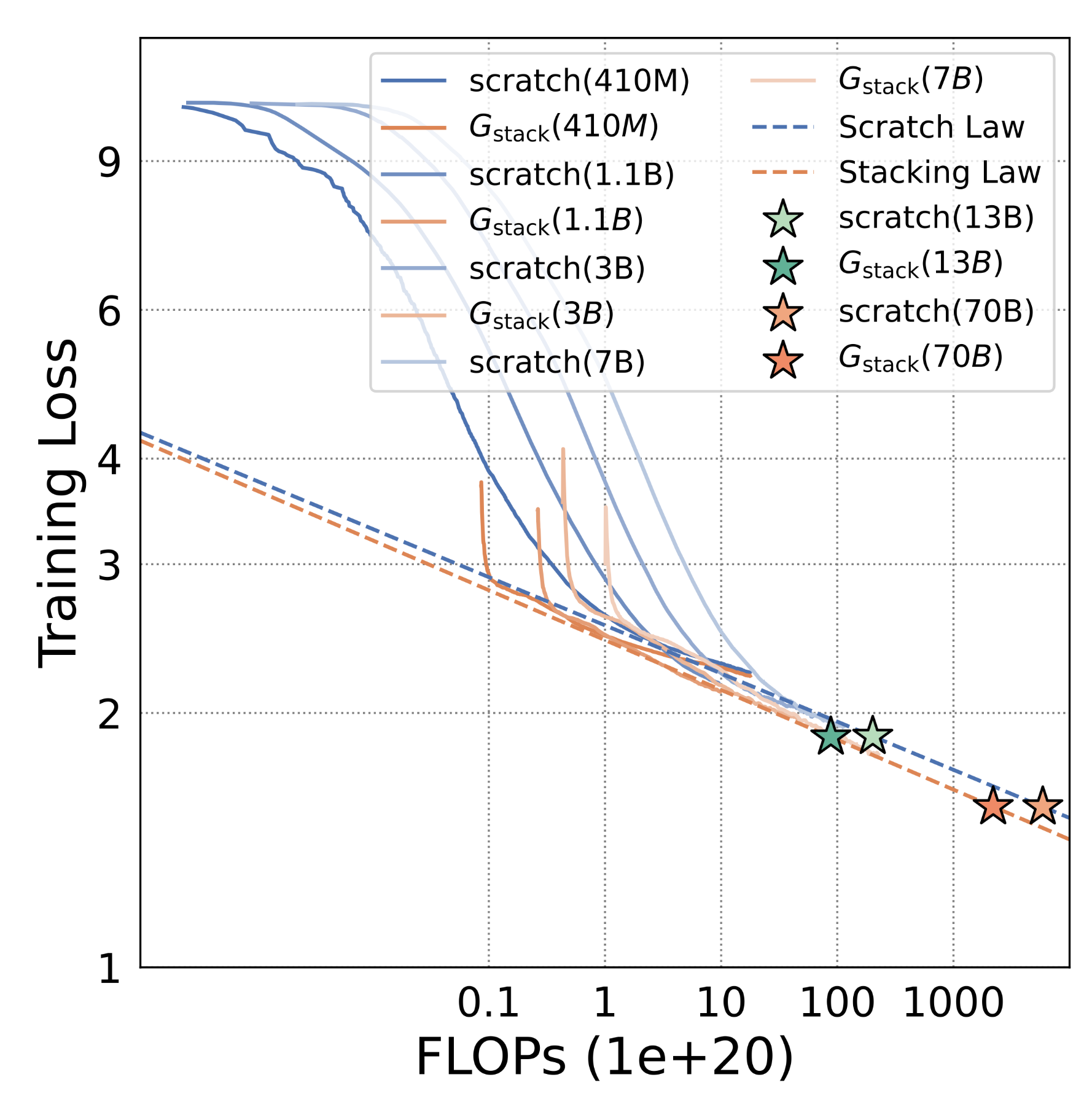
- 총 4개의 모델 학습 진행
-
410M, 1.1B, 3B, 7B
-
Chinchilla Scaling Law를 이용하여 Loss curve에 대한 fitting 시도
-
기존 Chinchilla Scaling Law 대비 Stack이 더 효율적으로 성능 개선이 가능함을 보임
- 비슷한 연산량에서 더 높은 성능(더 낮은 loss) 도달 가능
7. Scaling Law
Scaling Factor
-
기존의 데이터수 D, 연산량 N 이외에도 두가지 factor가 존재
- stacking 시점 d, stacking 횟수 g
-
stacking 시점 d
-
small model을 훈련시키는 데이터의 크기
-
small model 훈련에 N을 소모하는 것보다, 조금 훈련시킨 후 stacking하여 큰 모델을 훈련하는데 N을 소모하는 것이 효율적일 수 있음
-
-
stacking 횟수 g
-
stacking의 횟수가 많아진다 = larger model의 크기가 커진다 = scaling law에서 학습 iteration(학습 token 수)가 감소한다
-
즉, g는 기존 scaling law에서 model 크기와 연관됨
-
Stacking 시점 d
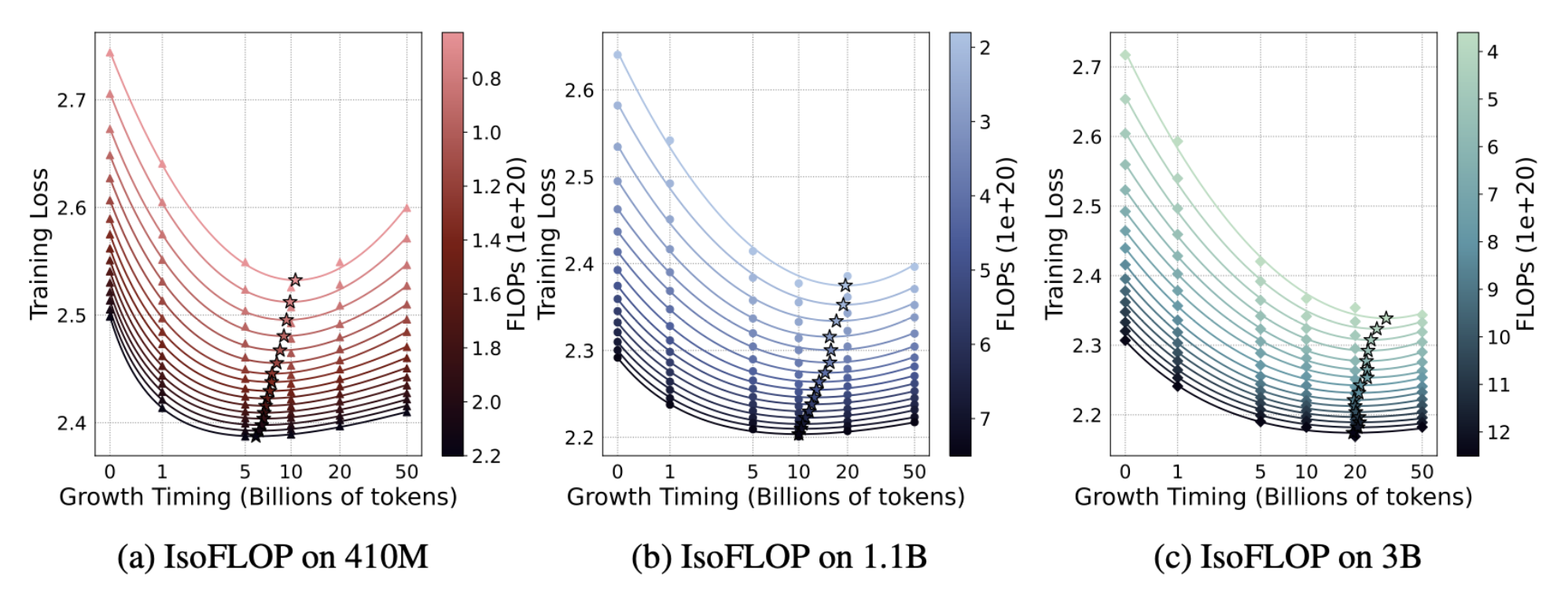
- stacking 횟수를 4로 고정하고 실험
Stacking 횟수 g
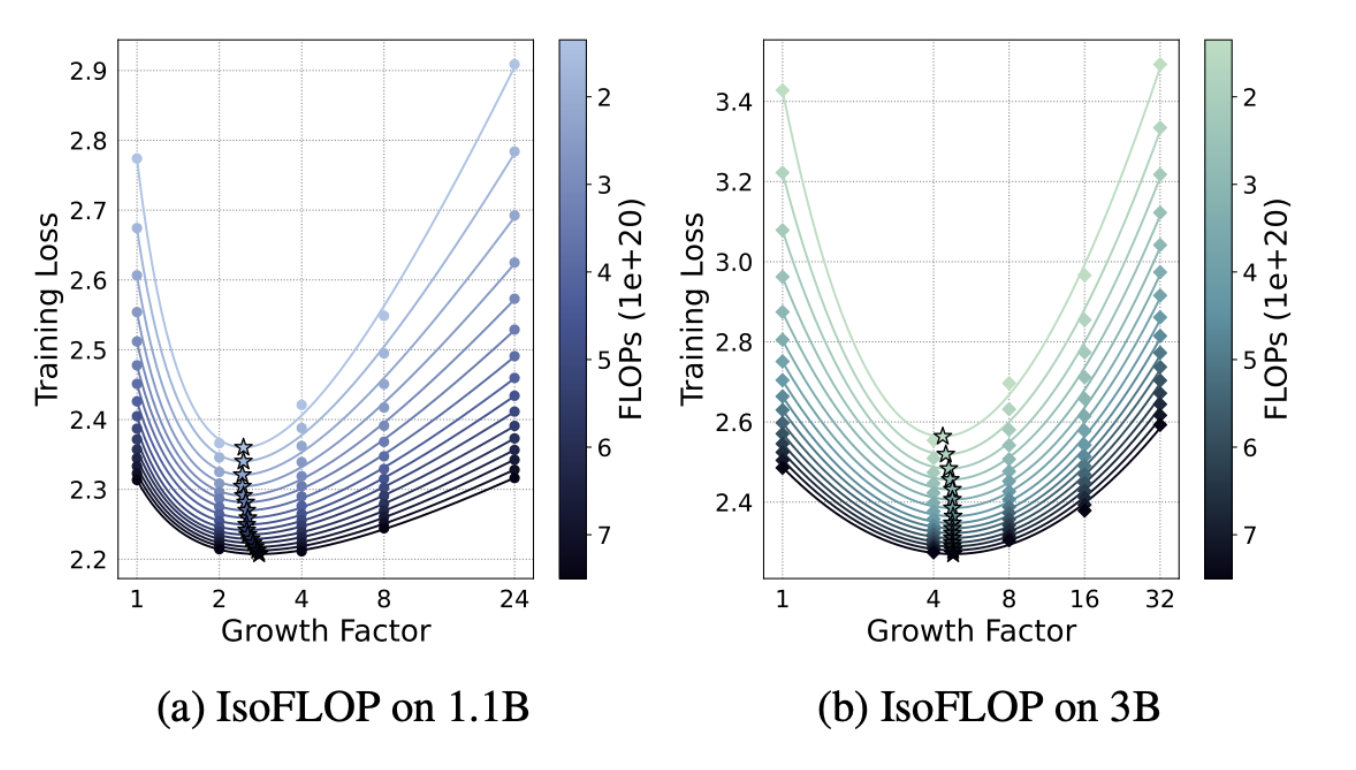
-
1.1B 모델과 3B의 base model을 이용하여 stacking 횟수를 달리하며 실험 진행
-
실험결과 모델 크기에 따라 차이가 존재
- 모델 크기가 클 수록 g가 커지는 것이 효과적
-
연산량에 따른 차이는 존재 X