Step-DPO : Step-wise preference optimization for long-chain reasoning of LLMs

논문 정보

Date: 2024-07-23
Reviewer: 전민진
Property: Reasoning, Reinforcement Learning

Abstract

기존 LLM이 mathematical reasoning를 푸는 것은 큰 challenge, 이를 개선하기 위해 human feedback을 바탕으로 모델의 robustness와 factuality를 향상시키려 함
이러한 방법론 중 하나인 DPO의 경우, 틀린 답변에서 디테일한 에러를 식별하기 어렵다는 한계가 존재
이를 개선하기 위해, 전체적으로 답변을 평가하기 보다 각각의 reasoning step에 대해 preference optimization을 하는 방법론인 Step-DPO를 제안
- Step-DPO를 위해 data를 구축하는 파이프라인을 개발, 이를 바탕으로 10K의 step-wise preference pair를 수집
  - 데이터를 수집하다 보니, GPT-4나 human이 만든 data보다 self-generated data가 더 효과적임을 알게됨
    - 전자는 학습하는 모델 입장에서 OOD의 성격을 지니기 때문
실험 결과, 기존의 DPO보다 더 높은 성능을 보이고, 특히 Qwen2-72B-Instruct에 적용했을 때, MATH, GSM8K데이터셋에 대해 각각 70.8%(+1.4), 94.0%(+1.6)의 성능을 보임

Introduction

기존에는 alignment를 강화하기 위한 SFT 단계에서의 여러 data augmentation techinque들이 제안됨
하지만 이러한 SFT 과정에서 hallunication을 야기할 수 있음
- 성능이 일정 수준 이상 향상되지 않음
- 이에 대한 원인으로는, 기존의 논문(ORPO)에서 언급한 preferred output에 대한 확률이 증가하면서 undesirable output의 확률도 증가하기 때문으로 추정
  - 이 경우 long-chain reasoning에서는 오류를 만들 확률이 높아짐
- 그래서 undesirable output의 likelihood를 억누르는 방법이 필요
최근, DPO가 여러 chat benchmark에서는 효과적이었으나, long-chain mathematical reasoning에서는 저조한 성능 향상을 보임
- 아래 그림을 보면, vanilla DPO는 preferred와 undesirable output을 잘 구별하지 못함
- 또한 vanilla DPO는 reward margin(perferred와 undesirable output사이의 reward gap)이 제한적임( = 성능이 일정 시점에서 정체됨)

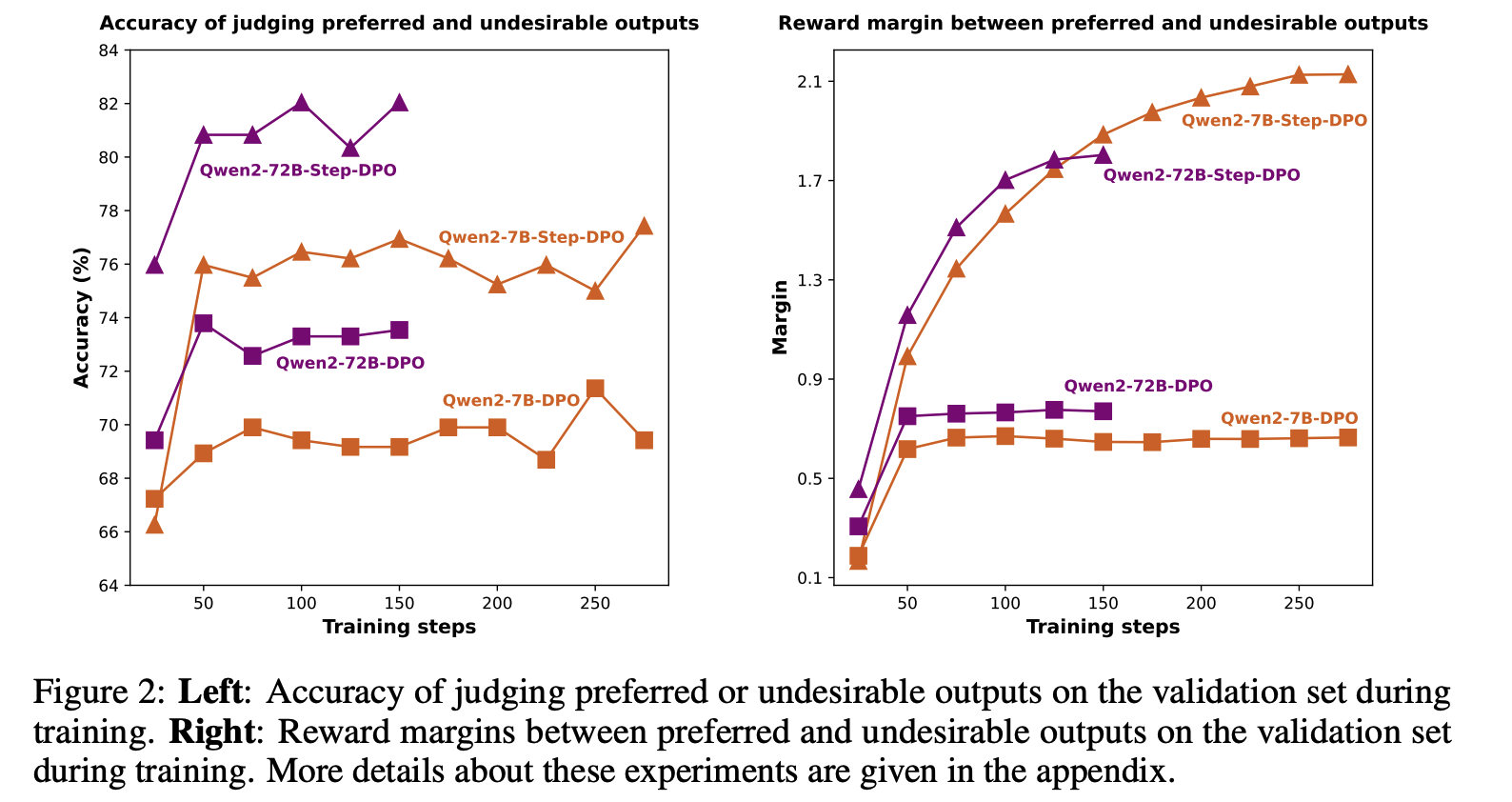
⇒ vanilla DPO는 틀린 답변에서 디테일한 오류를 잡아낼 수 없고, reasoning ability의 향상을 방해

본 논문에선, Step-DPO를 소개, 중간의 각 reasoning step을 preference optimization의 basic unit으로 상정
- Step-DPO에서는 문제와 초반의 correct reasoning step이 주어졌을 때, correct reasoning step을 선택하고, incorrect step을 reject하도록 학습하는 것이 목표
- Step-DPO로 학습하기 위해 다음과 같은 형식의 10K크기의 데이터셋을 구축
  - (mathematical problem, prior reasoning steps, the chosen step, rejected step)

Mathematical reasoning
- CoT
- Data augmentation for SFT
- Use external tool (e.g., Python)
- Continued pre-training on extensive, high-quality math related datasets
- RLHF relying on the quality of the reward model

Step-DPO

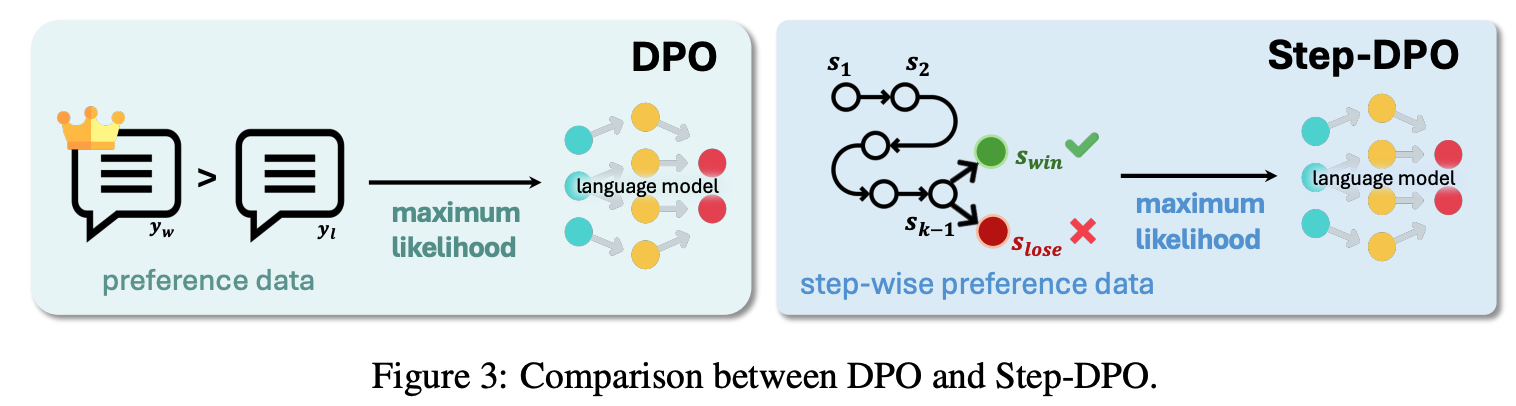
Step-wise formulation

DPO
- input prompt x, preference data pair (y{win},y{lose})가 주어질 때, DPO는 preferred output y_win의 확률을 높이면서 undesirable output y_lose의 확률은 낮추려고 함
- DPO의 경우, incorrect answer안에 일부 맞는 reasoning step이 있어도 전체를 reject하도록 학습되기 때문에 학습하면서 상당한 noise, 악영향을 끼침

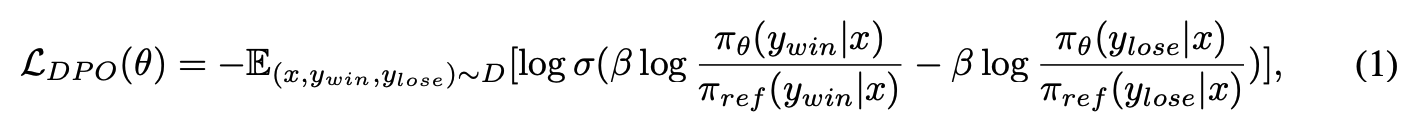
Step-DPO
- answer y를 reasoning step의 sequence y=s_1,…,s_n으로 쪼개서 생각
- Step-DPO에서는 correct next reasoning step s{win}의 확률을 높이고, incorrect next reasoning step s{lose}의 확률을 낮추는 것을 목표로 학습

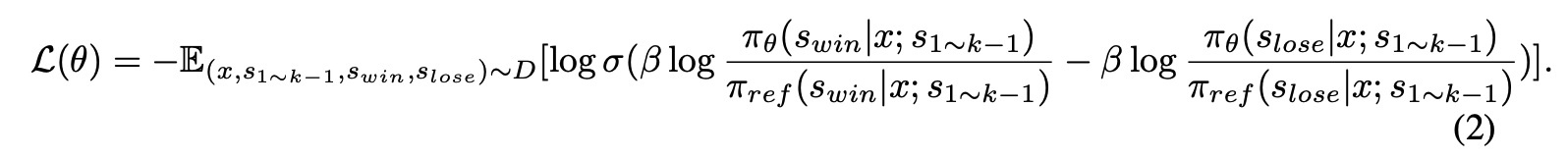
In-distribution data construction

Step-DPO로 학습하기 위해선 step-wise preference dataset이 필요
- 각 데이터는 다음의 4가지 entity로 구성됨
  - prompt x
  - initial reasoning steps s{1\sim k-1}=s_1,…,s{k-1}
  - preferred reasoning step s_{win}
  - undesirable reasoning step s_{lose}

이를 위해 3가지 단계(error collection, step localization, rectification)로 구성된 파이프라인을 제안

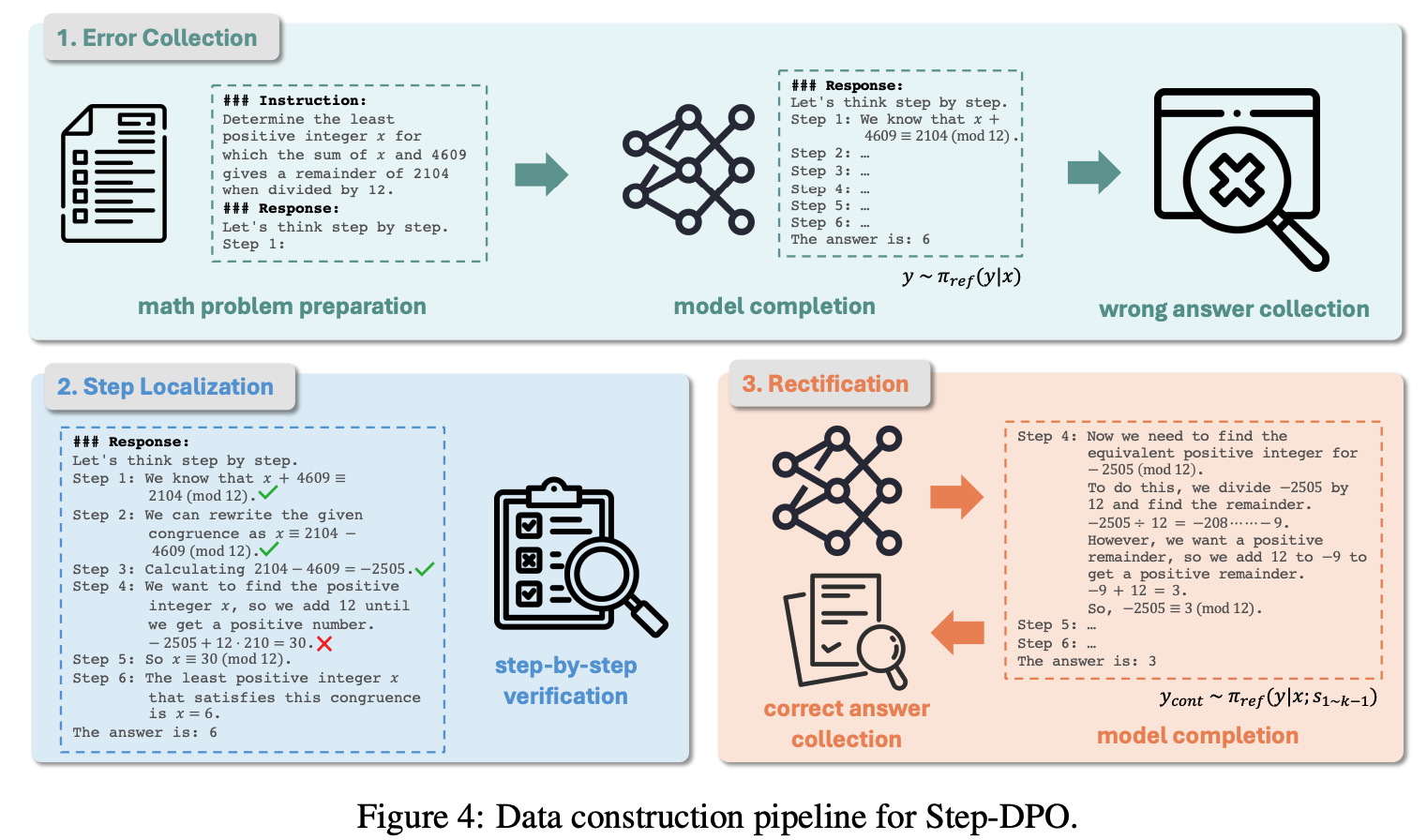
Error collection
- 우선 수학 문제와 정답으로 구성된 D_0={(x,\hat y)}를 수집
  - x는 reference model을 infer할 때 prompt로 사용
- inference 전에, step-wise Chain-of-Thought prefix를 추가
  - “Let’s think step by step. Step 1:”
  - 이를 통해 각 step이 명시적으로 step i 다음에 작성되게 됨
- 이러한 prompt를 바탕으로 final answer(model generated answer) y를 수집, 그중 오답인 y를 모아서 D_1={(x,\hat y, y)}를 구축
Step Localization
- D_1에서 수집한 sequence of reasoning step을 바탕으로, 각 step이 맞는지를 확인, 최초로 error가 발생한 지점을 k로 표기
  - GPT-4 혹은 사람을 써서 함
- sk를 틀린 reasoning step s{lose}로 사용
- D2={(x,\hat y, s{1 \sim k-1},s_{lose})}로 formulation
Rectification
- reference model에 prompt x와 preceding correct reasoning step s{1\sim k-1}를 여러 답변을 sampling(y{cont})

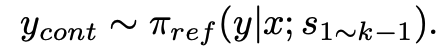
- 정답과 일치하는 답변만 가지고, 남아 있는 output중에서 y_{cont}에서 첫번째 reasoning step을 s_{win}으로 선택 최종 데이터셋 D=\{(x,s_{1 \sim k-1},s_{lose},s_{win})|x\in D_2\}를 구축

- 다만, 최종적으론 정답을 내놓더라도 중간과정이 틀릴 수도 있기 때문에, s_win이 틀린 경우가 있는지 GPT-4나 사람으로 검수

  - (이 과정은 appedix에 쓴다 했는데, 아직 appendix가 없음.. 쓰는 중인듯..)

**이렇게 데이터를 구축할 때의 키는 in-ditribution data를 사용해야한다는 것

만약 s_win을 구축할 때, reference model이 아니라 사람이나 GPT-4를 사용하게 된다면, 자기가 아닌 모델로 수정한 답변은 현재 모델에선 낮은 prob를 가질 수 있고, 이를 높은 확률이 되도록 학습하는 것은 gradient decay issue때문에 어려울 수 있음
- 이것도 appendix에서 다룬다는데 아직 없음.
결론적으로, self-generated in-distribution data를 사용하는게 human preference와 alinging되도록 학습할 때 효과적.

Experiments

Experimental setup

Network architecture
- Qwen2, Qwen1.5 series, Meta-Llama-3-70B, deepseek-math-7b-base를 기반으로 실험
Dataset
- In SFT
  - MetaMath, MMIQC to infer step-by-step responses with DeepSeek-Math
  - 최종 답이 틀린거는 빼고, 374K SFT data 수집
    - 이 중에서 299K를 SFT에 사용하고 나머지(75K)는 Step-DPO할 때 사용
- In Step-DPO
  - 위에서 남겨 놓은 SFT data와 AQuA의 subset를 합쳐서 사용
  - 위의 파이프라인대로 수행한 결과 최종적으로 10K의 pair-wise preference data를 구축
- In evaluation
  - MATH, GSM8K, AIME, Odyssey-MATH로 평가
    - math가 5000개의 데이터, gsm8k가 1319개.
    - math가 더 어려운 데이터셋
    - AIME(American Invitational Mathematics Examination)
    - Odyssey-MATH는 어려운 문제에서의 reaosning 능력을 평가
Implementation Details
- In finetune
  - 299K dataset으로 학습, 7B는 3 epoch, 30B이상은 2 epoch
  - batch size 256, lr 5e-6, optimizer AdamW, linear decay with warmup ratio 0.03
  - DeepSpeed ZeRO3 with CPU offload
- In Step-DPO
  - 10K dataset, 7B는 8 epoch, 30B 이상은 4 epoch
  - batch size 128, lr 5e-7, beta 0.5(72B에서는 0.4), AdamW, cosine learning rate scheduler with warmup ratio 0.1

Result

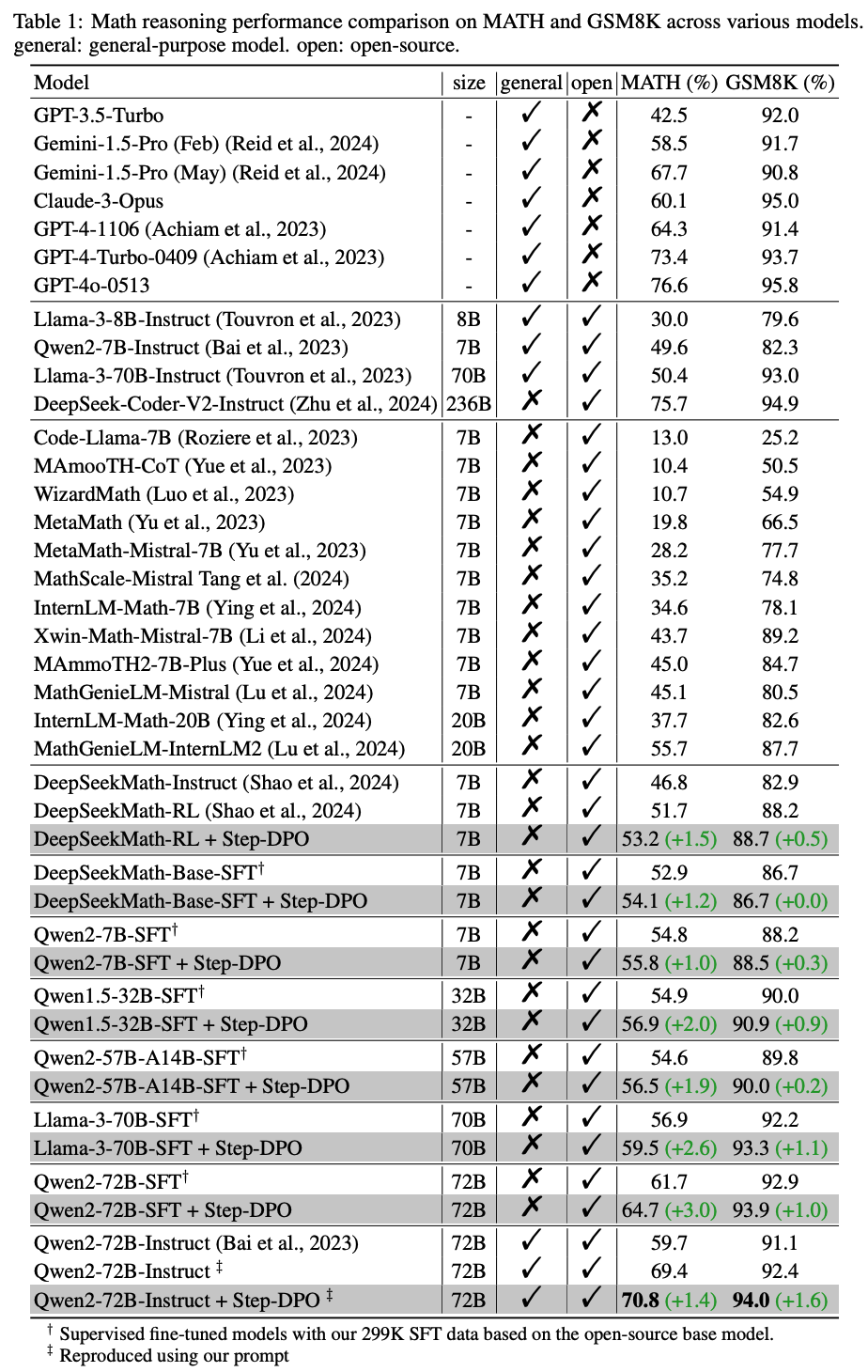
어떤 크기의 모델이든, Step-DPO를 했을 때 성능이 향상됨
- SFT에서 도달할 수 없었던 성능을 뛰어넘을 수 있게 해주는거 같다고 함..

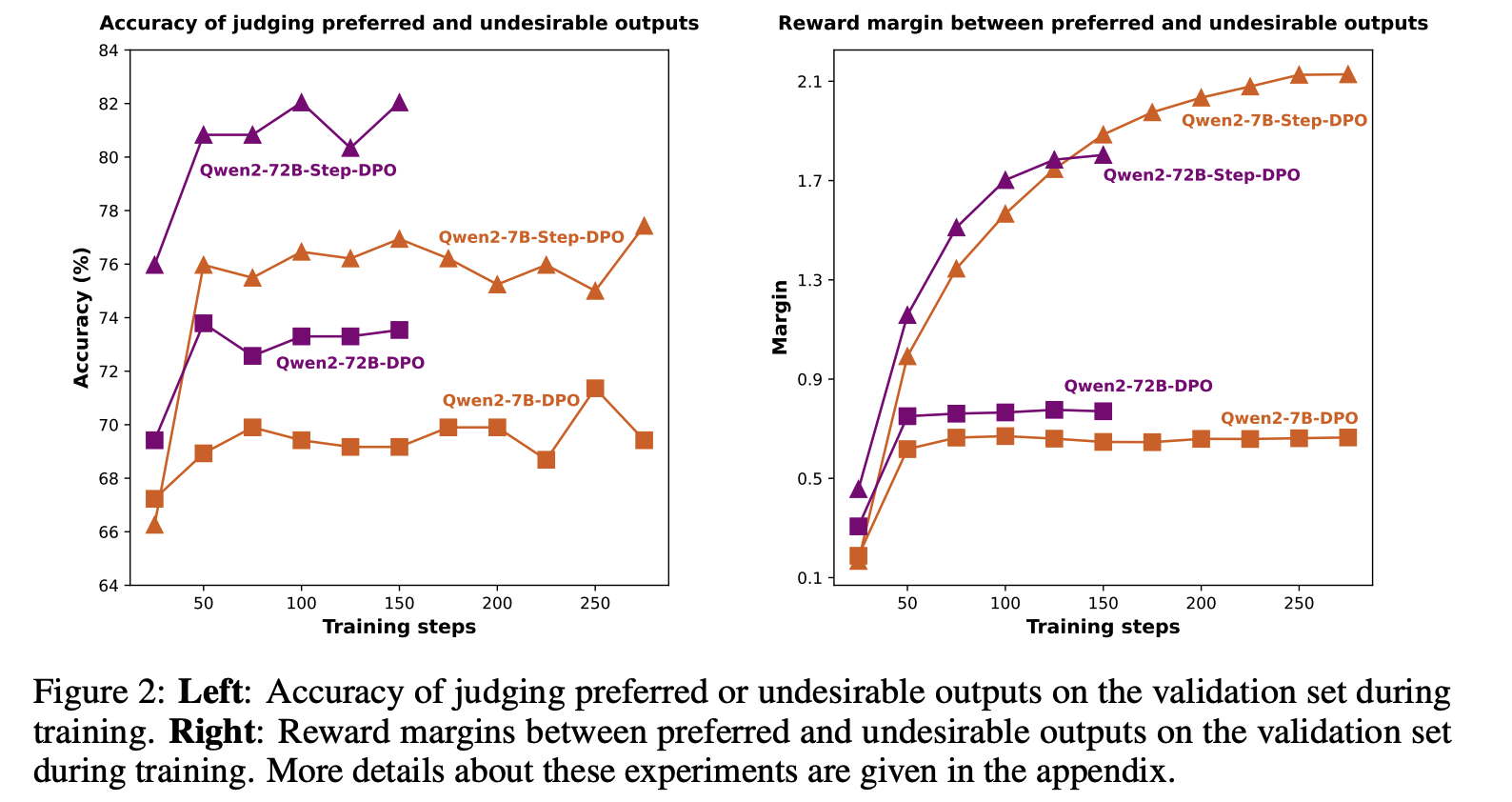
AIME 2024, Odyssey-MATH에 대한 실험..?이라고 하는데 자세한게 안나와 있음. 암튼 DPO보다 우월한 성능을 보인다!

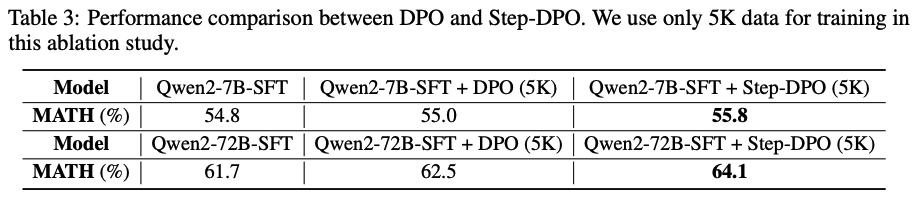
이 장표 역시 MATH test datset에 대한 DPO와 step-DPO의 성능을 보여줌

Ablation study

Out-of-Distribution vs In-Distribution Data
- ID로 하는게 성능이 더 높았음.

Demonstrations

Step-DPO로 학습하니까 reasoning step에서 detailed error가 발생하지 않았다!

Summary

최종 답만을 기반으로 DPO를 하는 것이 아니라, 중간 과정도 신경쓰는 step-DPO를 제안
모델 크기, 종류와 상관없이 step-DPO를 사용하는 것이 성능 향상에 도움이 됨
아이디어 자체는 훌륭하나 아직 쓰는중?이라 그런지 실험이 살짝 부실
어떻게 reasoning step 중간에서 feedback을 줄 수 있을지가 궁금했는데, 이런식으로 간단?하게 해결할 수 있다는 것을 알게됨.

Abstract

Introduction

Related Works

Step-DPO

Step-wise formulation

In-distribution data construction

Experiments

Experimental setup

Result

Ablation study

Demonstrations

Summary