Training Language Models to Self-Correct via Reinforcement Learning

Created on September 23, 2024

2024   ·   agi   alignment   fine-tuning   gpt   language-model   llm   paper-review   reinforcement learning   reinforcement-learning   vision   ·   paper-reviews

논문 정보

  • Date: 2024-09-23
  • Reviewer: 준원 장
  • Property: Reinforcement Learning, AGI

1. Introduction

  • 최근에 베포된 LLM은 ‘알고리즘=문제수행능력’을 안정적으로 진행하지 못함 ⇒ test time query에 대해서 LLM이 자체적으로 생성한 response를 ‘self-correct’하고 best-possible final response을 생성하는 action을 취하지 못함.

    • ‘self correction’에서 external input이 없는 setting을 ‘intrinsic self-correction’이라고 현재 LLM은 해당 문제에 취약하다는 선행연구가 존재함.

    • 논문에서는 ‘intrinsic self-correction’을 해결하고자 함.

  • 논문에서는 LLM이 위와 같이 어려운 문제를 풀때 “on-the-fly” setting으로 mistake를 해결하는 방법론을 연구하고자 함.

    • Snell et al., 2024에 따르면, LLM이 문제에 대한 오답을 내놓았을때 실제로는 정답과 관련 underlying “knowledge”을 가지고 있지만, 그것이 필요할때 정확히 elicit하고 draw inference하는 능력이 부족하다고 함

  • 그렇다면 기존 연구에서는 어떻게 LLM에서 self-correction abilities를 주입했을까?

    1. Prompt-engineering (Kim et al., 2023; Madaan et al., 2023)

    2. meaningful intrinsic self-correction을 수행하는데 한계가 존재함

    3. Fine-tuning (Havrilla et al., 2024b; Qu et al., 2024; Welleck et al., 2023; Yuan et al., 2024)

    4. inference시에 verifier, refinement model 같은 multiple model이 필요함

    5. self-correction training 중 oracle teacher model이 필요함

  • 저자들은 실험 가능한 2개의 baseline의 한계를 제시하면서 새로운 방법론을 제시함

    1. Rejection Sampling 기반의 STaR는 model이 correction을 수정하지 않도록 bias를 강화한다.
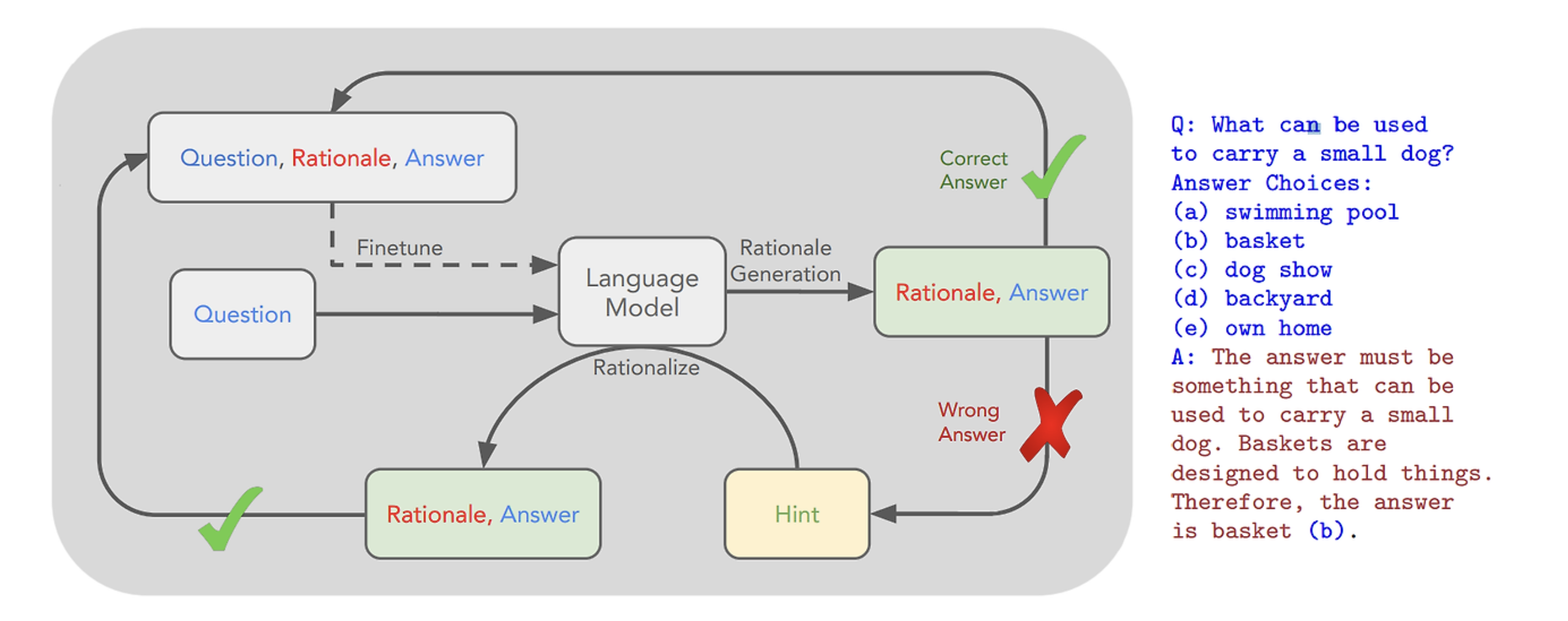
  1. minimal edit strategy는 self correction 능력을 주입하진 않지만, ‘ 두번째 generation에서 정답을 잘못 입력하는 학습을 억제한다.’ → suboptimal이며, distributional mismatch 환경에서 성능이 안좋아짐

  • 이를 해결하기 위해 논문에서는

    • self generated data로 학습이 가능한 multi-turn RL 방법론을 제시

#### Prompting for intrinsic self-correction

  • self-correction 과정중에 oracle answer을 활용하는 한계

  • first response를 생성할때는 weak prompt를 사용하고, self-correction시에는 strong prompt를 사용해 overestimate 문제

#### Fine-tuning for intrinsic self-correction

  • oracle feedback (revisions directly from human annotators & human)을 SFT에 직접적으로 활용한다는 한계

⇒ 본 연구는 learner가 직접 생성하는 training data만을 활용

3. Preliminaries and Problem Setup

Problem Define: External Feedback이 없는 intrinsic self-correction’ setup

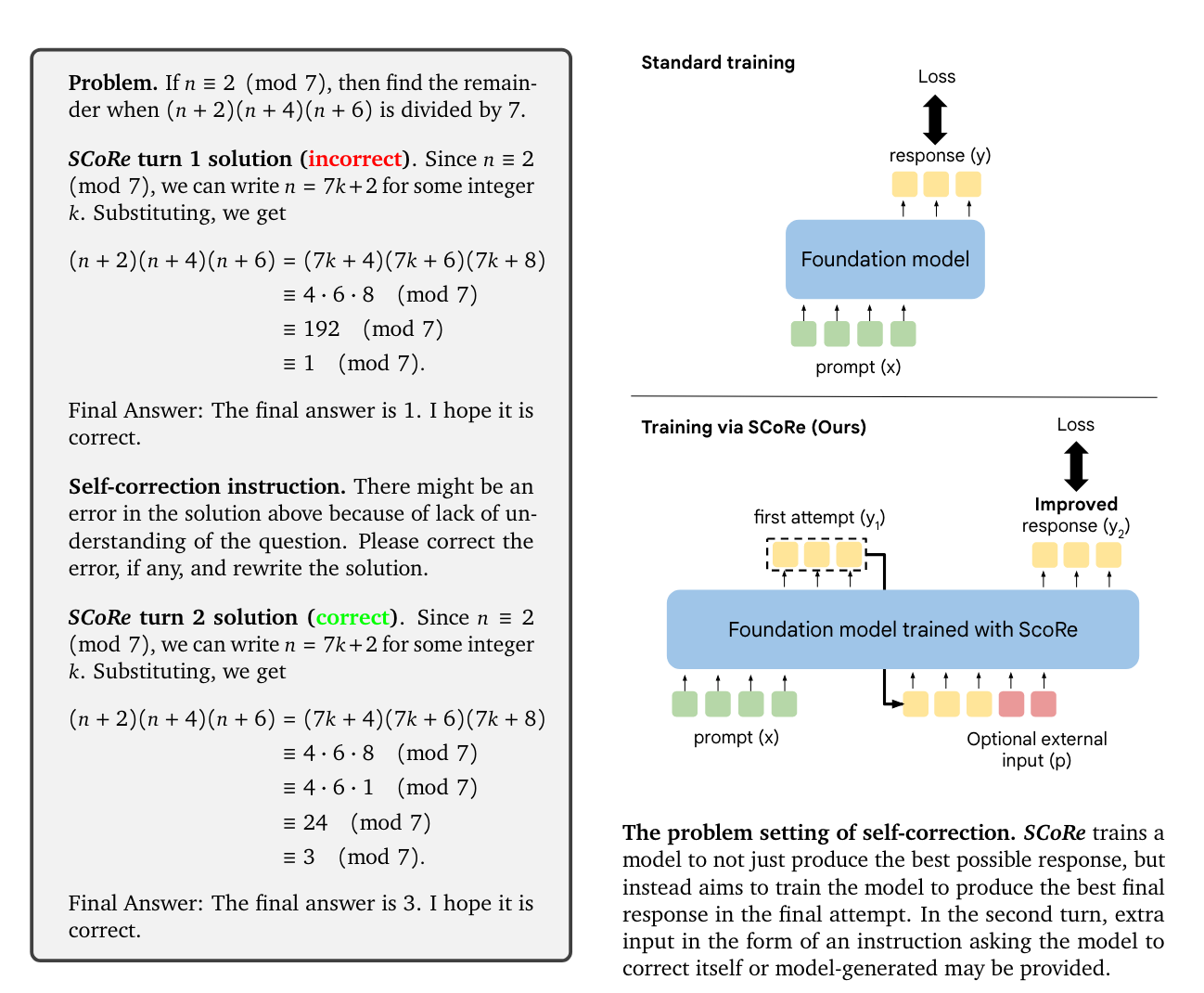
  • Setting

    • Multi-turn RL (2-turns)

    • Dataset: \mathcal{D} = {(\mathbf{x}i, \mathbf{y}_i^*)}{i=1}^{N}

    • What we want to train: LLM Policy \ \pi\theta(\cdot \mid [\mathbf{x}, \hat{\mathbf{y}}{1:t}, \mathbf{p}_{1:t}])

    • Reward Function: \text{verifier } r(\mathbf{y}, \mathbf{y}^*)

      • 당연히, inference time에는 접근할 수 없으며 모델이 추론을 통해서 mistake가 있는지 여부를 판단.

  • Standard SFT나 일반적인 RL tuning과는 달리, 여러 턴을 동시에 학습.

  • 중간 턴 응답 ŷ_{1:t}은 final reward의 intermediate context를 위해 간접적으로 supervised tuning됨.

  • A base RL approach for fine-tuning LLMs

    • on-policy gradient 학습 기법을 사용

    • REINFORCE with KLD penalty (PPO)

  • Metric

    • Accuracy@t1: 첫 번째 시도에서의 LM의 ACC

    • Accuracy@t2: 두 번째 시도에서의 LM의 ACC

    • Δ(t1, t2): 첫 번째와 두 번째 시도 사이의 LM의 ACC 순 개선, self-correction 효과를 측정

    • Δ^i→c(t1, t2): 첫 시도에서 틀렸지만 두 번째 시도에서 맞은 문제의 비율, self-correction이 해결할 수 있는 새로운 문제의 수를 측정

    • Δ^c→i(t1, t2): 첫 시도에서 맞았지만 두 번째 시도에서 틀린 문제의 비율, 모델이 정답을 이해하는 능력을 측정 (많이 떨어지면 덜 이해하는건가?)

4. Supervised Fine-Tuning on Self-Generated Data is Insufficient for Self-Correction

** #### ‘Intrinsic Self-Correction’ Setting이니 외부 model의 feedback 없이 base-model을 가지고 self correction하는 SFT하는 방법론을 돌려보면 어떨까?**

  • Baselines SFT

    • STaR

    • Pair-SFT

4.1. Analysis Setup: Methods and Dataset Construction

  • STaR ⇒ (1) base model로 two-turn self-correction traces를 생성함. (2) second attempts가 successfully하게 first attempt의 incorrect responses를 revise할 경우에만 filter

    • \mathcal{D}{\text{STaR}} := {(x_i, \hat{y}_i^{-}, \hat{y}_i^{+})}{i=1}^{N}, \text{ where } \hat{y}_i^{-} \text{ and } \hat{y}_i^{+} \text{is incorrect and correct answer}

      • 위의 설명 그대로 데이터셋 구축

⇒ Training 3 iterations of collecting and running SFT.

  • Welleck et al. (2023) ⇒ (1) base model로 two-turn self-correction traces를 생성함. (2) first attempts에서 pairing incorrect responses with correct ones 후 generates “synthetic” repair traces

    • \mathcal{D}{\text{SFT}} := {(x_i, \hat{y}_i^{-}, \tilde{y}_i^{+})}{i=1}^{N}, \text{ where } \tilde{y}_i^{+} \text{ is a random correct response for problem 𝒙} \ \text {randomly sampled from the set of all first-turn and second-turn responses produced} \ \text{by the model.}

      • two-turn self-correction traces에서 생성한 정답 중 랜덤하게 배치.

⇒ Training 1 epoch with SFT.

4.2. Empirical Findings

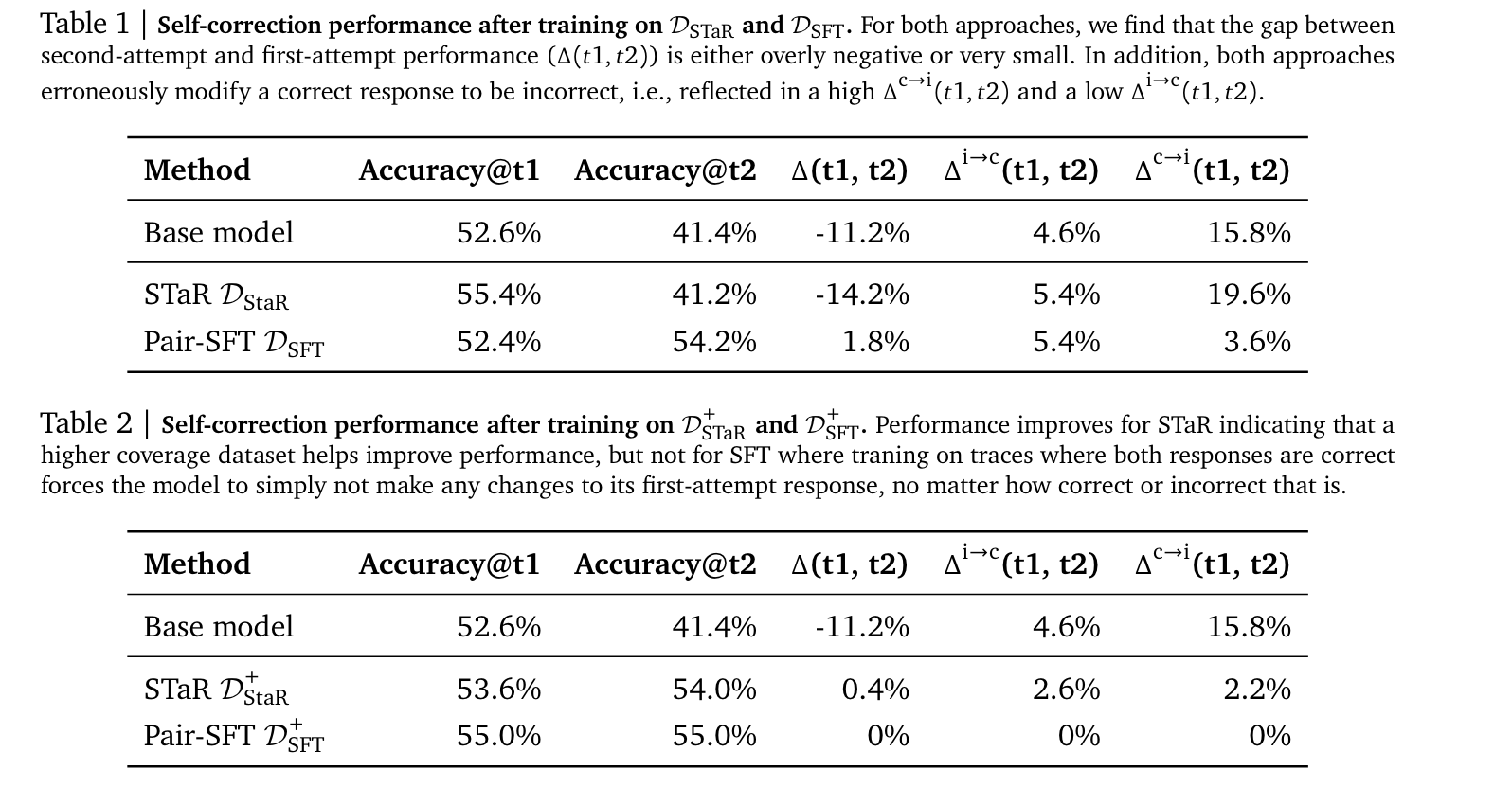
  • Pair-SFT로 학습하면 base-model 대비 의도한 self-correction 행동경향성이 도출됨. (Δ(t1, t2)의 증가, incorrect → correct의 증가 correct → incorrect의 감소)

  • STaR의 경우 오히려 self-correction이 전혀 일어나지 않고 있는데, 저자들은 ‘revision trajectories’가 limited된 space여서 그렇다고 함 (사실 뭔말인지 모르겠..)

  • Table 1에서 가장 큰 문제는 Correct를 Incorrect로 바꿔버린다는 것 (준원 생각: 사실상 self-correction이 아니라 그냥 무작위로 alignment를 하는것으로 보임), 저자들은 이런 경향성을 억지로 지워버리고자 2번째 attempts 모두에 대해서 correct response로 학습하는 Table2 결과를 내놓음

    • STaR는 self-correction을 거의하지 못하고, Pair-SFT는 아예 정답을 변경하지 않고 있음.

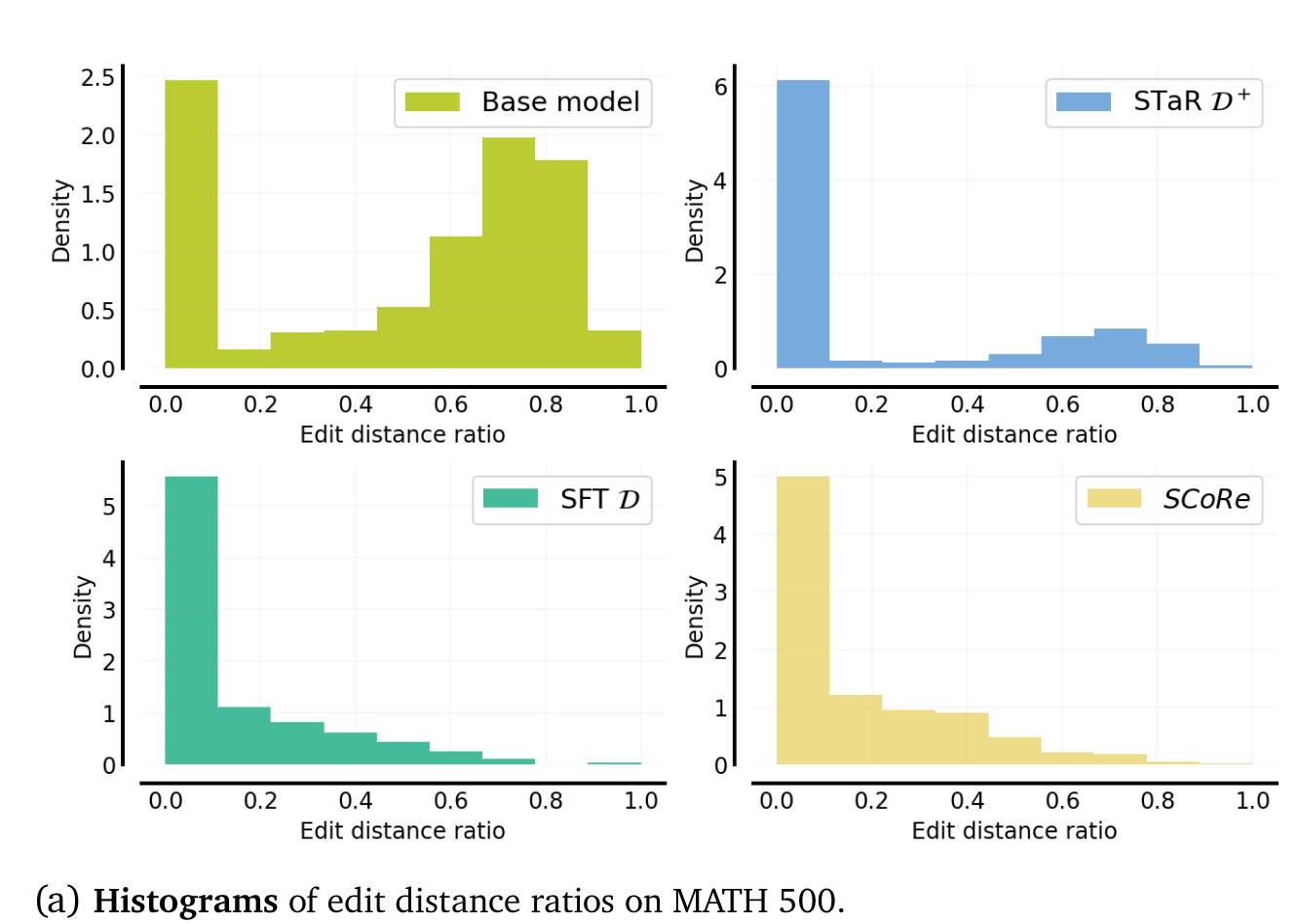
  • (제안한 방법론 SCoRe도 거의 변화가 없긴한데..) STaR D+, SFT D는 base model 대비 edit distance (first vs second response)의 차이가 거의 없는 것을 알 수 있습니다.

    • base model 대비 edit distance가 거의 없다 (만약 first attempt의 성능이 좋다면 위의 표가 납득이 가야하는데 그렇지 않으니, 문제가 있다라는 것을 보여주는 것 같습니다.)
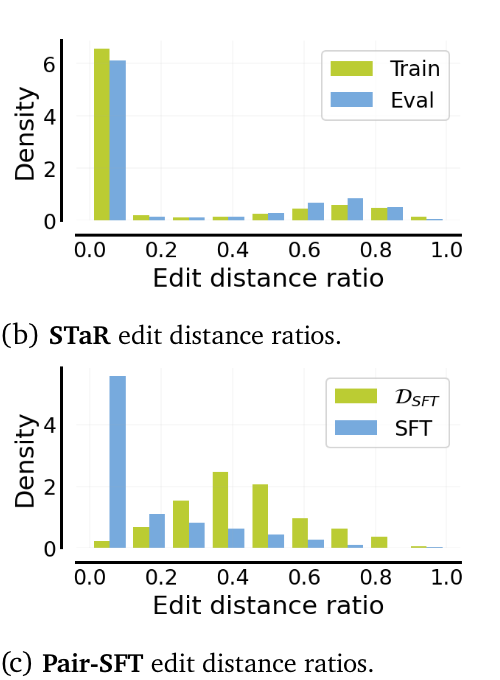
  • STaR D+와는 달리 SFT D는 training과 evaluation에서 edit distance (first vs second response)의 분포 차이가 많이 남.

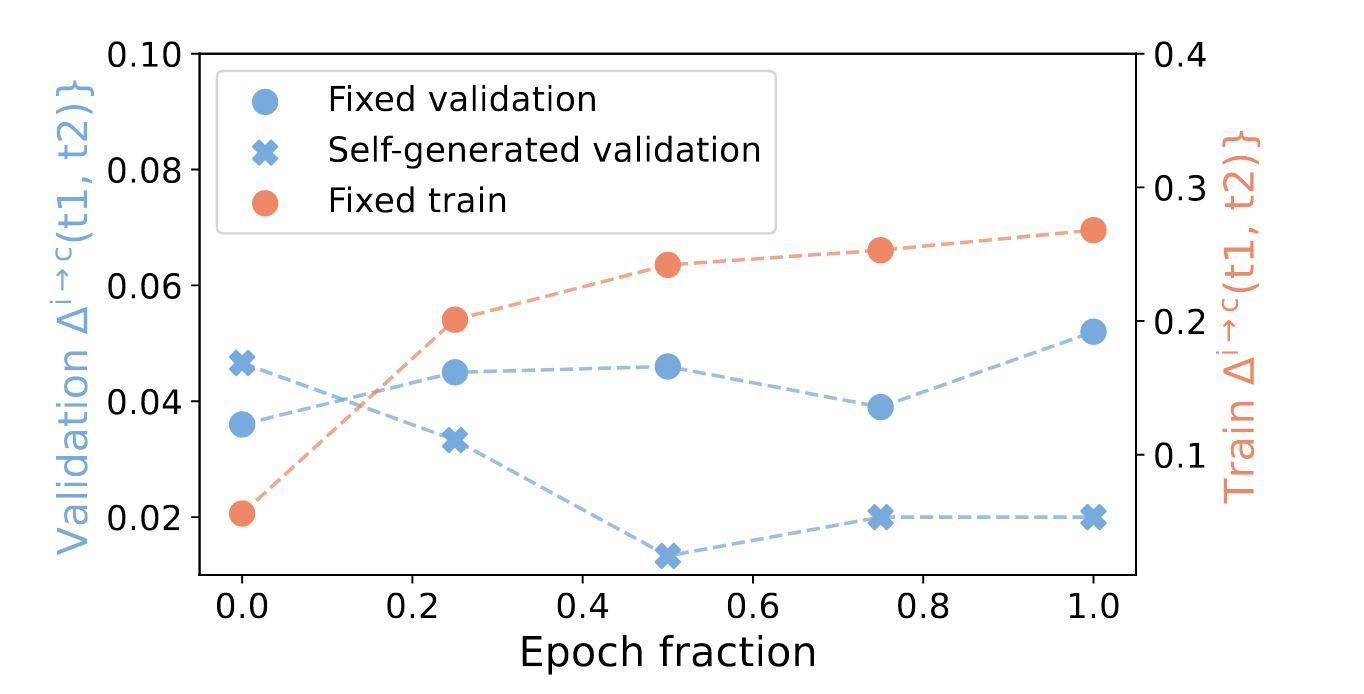
  • Pair-SFT에 대한 ablation

  • fixed ~: first response는 각 dataset에 있는 offline response를 그대로 condition으로 쓰는 setting

    • training은 당연히 dataset에 있는 걸 가져와서 사용해야 하니 Fixed train

  • self-generated: learner가 first response를 generating하는 setting

  • Pair-SFT에서 Training때처럼 fixed validation set으로 validation을 진행하면 성능이 지속적으로 유지되는 것을 알 수 있음

⇒ distributional shift는 self-correction에 있어서 중요한 issue이며, fixed offline dataset은 좋은 학습 데이터셋이 아니다.

Takeaways: Insufficiency of SFT (previous method)

  1. STaR D+는 distribution shift에는 강건한 대신 one mode of correction에만 collapse된다는 한계가 존재함.

  2. (i.e., correct → correct에서만 그나마 조금 작동함)

⇒ what we have to solve: amplification of certain pathological behaviors that seem promising on the training data

  1. Pair-SFT는 distribution shift가 있어 인해 (exploration은 좋아지나: 어찌저찌 성능은 좋아지나) 정작 LM의 first attempts에 대한 self correction 능력이 저하된다.

⇒ what we have to solve: distribution shift in training data

5. SCoRe: Self-Correction via Multi-Turn Reinforcement Learning

Key Challenges

  • 위의 mulit-turn RL을 활용해 학습을 진행하면 distributional shift를 해결할 수 있는건 수식적으로 당연

  • 실험을 진행

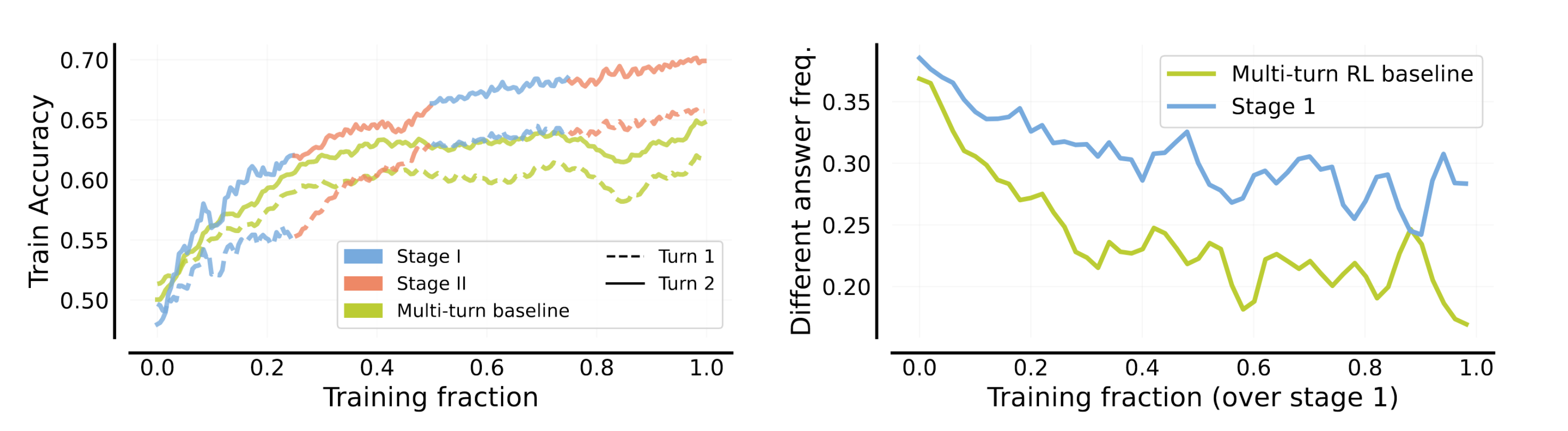
  • (left) first response과 second response의 train acc가 같은 방향으로 계속 움직이는 걸 알 수 있음

  • (right) 초록색 선을 보면 first response대비 second response가 얼마나 다른 answer를 생성하는가?인데, 학습을 지속할 수록 coupling된 정답을 생성하는 것을 알 수 있음

Why does this happens?

  • Data distribution내에서 LM이 취할 수 있는 optimal action은 2가지.

    1. first response에서 second response로 revise하도록 학습하거나 ⇒ Unseen Test distribution에서 generalization 시켜야할 정책.

    2. first response에서 최상의 응답을 생성한 다음 second response에서 수정하지 않도록 학습

⇒ Overparameterization된 LLM은 (Data distribution내에서 1,2가 둘다 최적이라고 리워드가 설계되어있고 그걸 그대로 학습을 하면) 1.에 대한 정책을 제대로 학습하지 못할 수도 있음.

**⇒ 과거의 주어진 attempts에 대해서 self-correcting하는 최적의 방법이 아니라, 현재 주어진 response를 개선하는 next response를 생성하라고 model에게 학습시켜야 함. **

Method

Objective

  1. (비유를 들면 prior distribution을 깔아줌으로써) LM이 first attempt distribution하에서 second distribution을 생성하도록 학습

  2. reward-shaping을 통해 bias model to self-correct

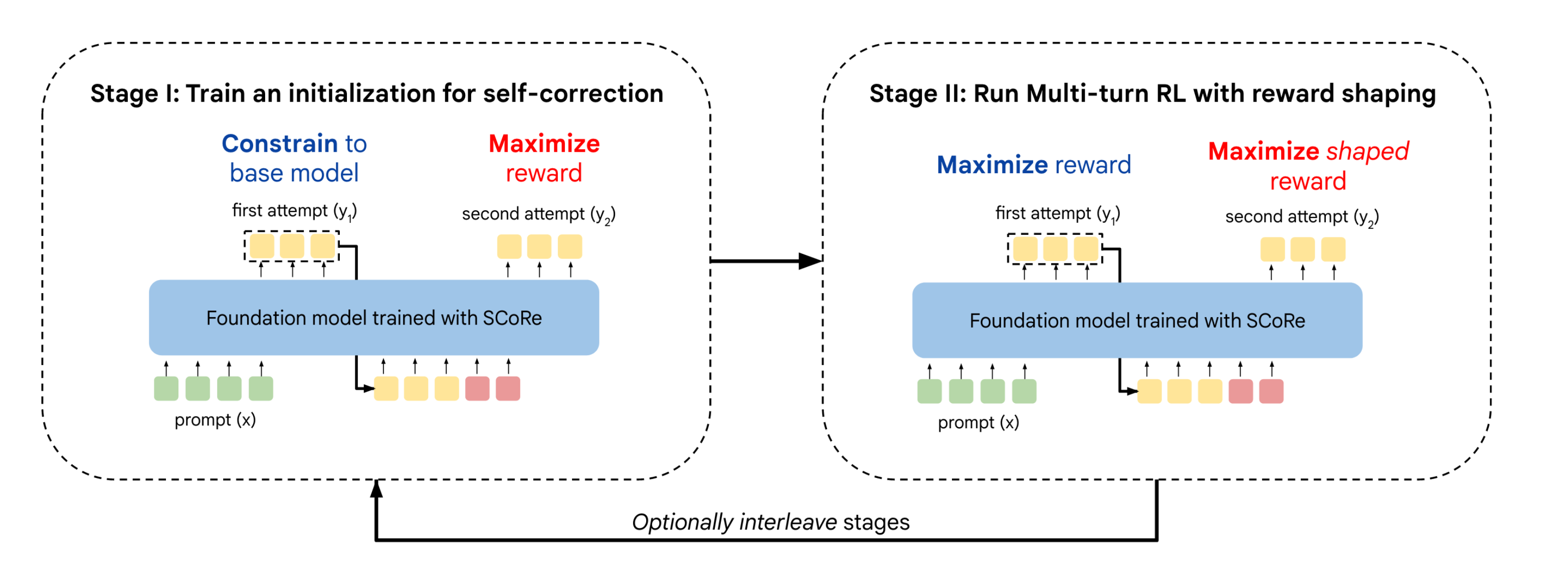
5.1. Stage I: Training a Model Initialization to Prevent Collapse

  • one-mode collapse를 방지하기 위해 RL로 학습 진행

  • second response에서 높은 reward revision이 이루어지도록 하는 동시에 KLD를 사용하여 first response distribution이 base-model 최대한 가깝게 제한함

    • 수정할 게 거의 없는 first response을 더 나은 second response으로 수정할 수 있다는 점에서 최적이 아닌 것처럼 보이지만, 목적은 first response와 second response를 decoupling하는데 있음

      • second response에도 KLD term을 두는데 weight를 1/10으로 둠

    • Untitled 을 보면 Stage 1이 당연하게도 first response와 second response에 대한 mode collapse 문제를 해결해주는데 도움이 됨

5.2. Stage II: Multi-Turn RL with Reward Shaping

  • first response와 second response에 대한 reward sum을 max하도록 training

  • Reward shaping to incentivize self-correction

    • LM이 self-correction solution을 학습할 수 있도록 bias를 걸어주는 작업을 진행

    • second response에 아래의 bonus를 더해줌. (Δ^i→c(t1, t2)와 Δ^c→i(t1, t2)에 유리한 reward shapping)

      • \hat{b}(y2 \mid y_1, y^) = \alpha \cdot (\hat{r}(y2, y^) - \hat{r}(y_1, y^*))

    • training set에 mode collapse를 완화해줄 것을 기대

6. Experimental Evaluation

  • Tasks &. Models

    • MATH ⇒ Gemini 1.5 Flash

      • training set with 4500

    • HumanEval, MBPP-R (offline test: incorrect first-attempt is generated by PaLM2) ⇒ Gemini 1.0 Pro

      • training with MBPP

  • Results

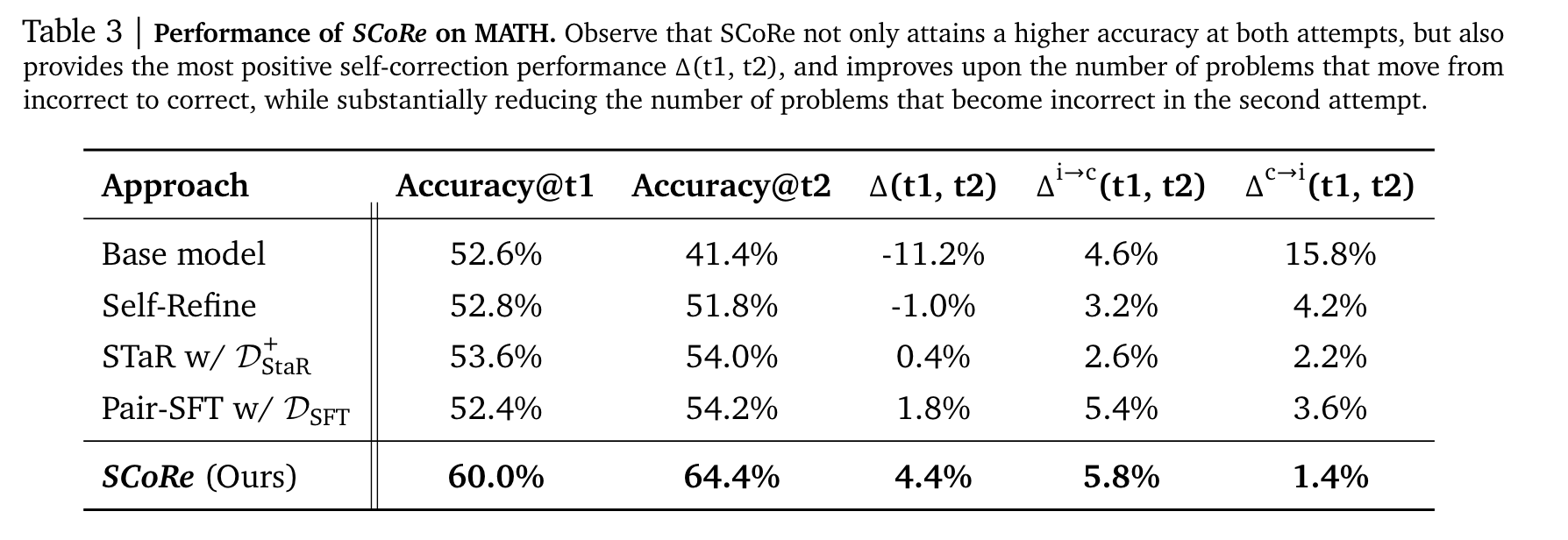
  • base model 대비 Δ(t1, t2) 15.6%, Accuracy@t2 23.0% 증가

  • 가장 고무적인건 의도한 self-correction이 동작한다는 점

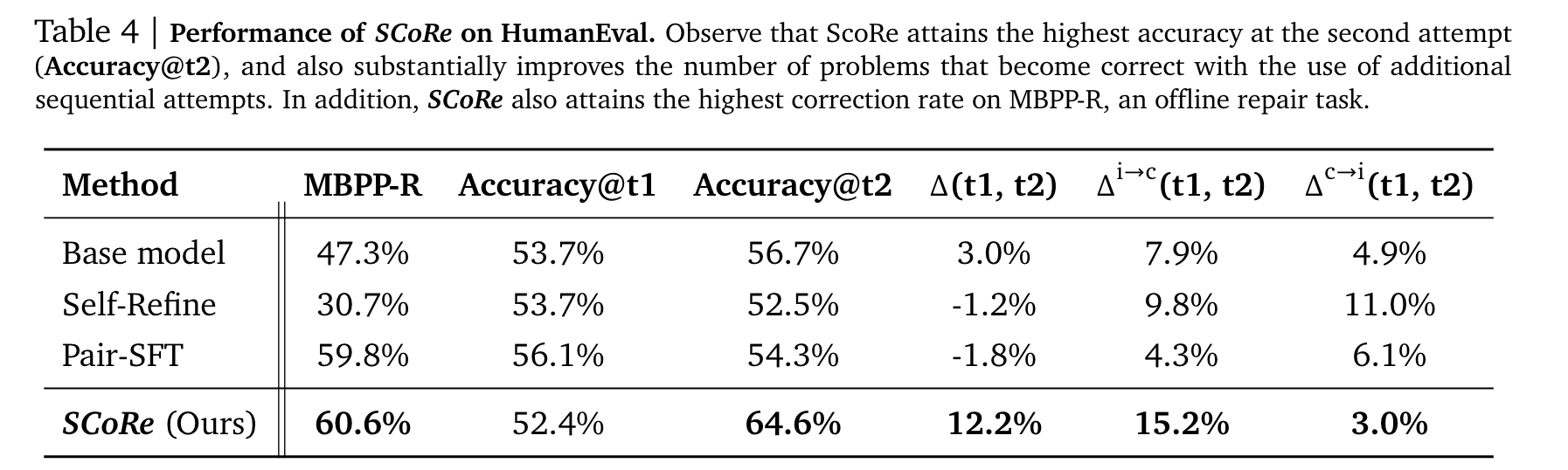
  • Pair-SFT같은 경우 offline setting에서만 성능이 좋은 반면, SCoRe는 self-generated setting에서 self-correction(12.2% intrinsic self-correction delta)을 통해 성능 증가를 가져오는 것을 알 수 있음

    • Accuracy@t1이 상대적으로 낮은건 KLD 때문이 아닐까?

  • (w/o m.t.t) single turn으로 학습을 진행하면 당연히 Accuracy@t1은 높지만 그 외의 지표는 떨어지고,

  • (w/o s1, rs) stage 1이나 reward shaping을 제거하면 의도한 self-correction을 수행하지 못해 Accuracy@t2와 net increase acc 역시 하락하는 것을 확인할 수 있다.

  • (w STaR) 마지막으로 stage 2에서 on-policy가 아닌 offline data로 학습하면 distributional shift때문에 spurious solution을 학습해 성능이 하락한다고 논문에서 설명하고 있다.

7. Discussion

  • 논문에서도 언급하지만 1 round 이상 iterative correction 못한 것을 limitation으로 이야기하고 있음

  • ChatGPT나 시중에 나온 chatbot들을 쓰면서 몇 turn 대화를 이어서 진행할 때 계속 같은 해답을 내주는거에 대해서 왜 그럴까?에 대한 대답과 그 해결책을 제시해준 논문이었다.