BLOCK DIFFUSION: INTERPOLATING BETWEEN AUTOREGRESSIVE AND DIFFUSION LANGUAGE MODELS

Created on August 05, 2025

2025   ·   attention   diffusion   diffusionlm   generative   gpt   language-model   llm   paper-review   transformer   ·   paper-reviews

논문 정보

  • Date: 2025-08-05
  • Reviewer: 상엽
  • Property: DiffusionLM, LLM

Introduction

Diffusion 모델이 가진 한계점

  1. 현재 대부분의 diffusion 모델의 경우 고정된 길이의 답변만을 생성.

  2. Bidirectional context를 사용하기 때문에 KV 캐시와 같이 AR 추론에서 효율적인 방법들을 사용할 수 없음.

  3. Standard metric (e.g. perplexity)에서 여전히 낮은 성능을 보임.

→ Block Discrete Denoising Diffusion Language Models (BD3-LMs)

BD3-LMs

Interpolation between discrete diffusion and autoregressive model

  • Block diffusion model: semi-autoregressive model

  • Inter-Block: Block을 생성하는 과정은 AR 과정으로 모델링

  • Intra-Block: 이전 block이 주어질 경우, 현재 block 내부는 discrete diffusion 과정으로 모델링

Block Diffusion 모델이 가진 Two challenges를 발견: 핵심!!

  • Block diffusion을 학습하기 위해서 두 번의 forward pass가 필요함. → 계산량 증가

  • 높은 gradient variance로 인한 성능 저하

→ 지금은 이해가 어려우니 뒤에서 확인

Contribution

  • Block discrete diffusion language model 제안. 기존 diffusion 모델과 달리 variable-length generation과 KV caching을 지원

  • 학습 시 토큰 배치를 효율적으로 활용할 수 있도록 block diffusion model을 위한 훈련 알고리즘 제안 (Challenge 1)

  • Gradient variance가 diffusion 모델 성능의 제한 요소임을 밝힘 + 데이터 기반 노이즈 스케줄로 해결 (Challenge 2)

  • 성능 향상!

BACKGROUND: LANGUAGE MODELING PARADIGMS

notation

  • scalar discrete random variables with V categories as ‘one-hot’ column

  • \Delta^V: simplex 공간

  • m \in \mathcal{V}: [MASK] token’s one-hot vector

AUTOREGRESSIVE MODELS

DISCRETE DENOISING DIFFUSION PROBABILISTIC MODELS (D3PM)

  • p: denoising, q: noising

  • s(j) = (j-1)/T, t(j) = j/T (이후에 j는 생략!)

    • 알파벳 순서대로 s가 앞 t가 뒤, s → t 과정은 noise를 더하는 과정

  • D3PM framework: q를 Markov forward process, 각각의 토큰에 대해 독립적으로 아래의 식을 진행

    • Q_t의 예시

      • Uniform replacement

      • Masking 기반: \beta_t 확률로 [MASK] 토큰으로 변경

  • 이상적인 diffusion model p{\theta}는 q의 역방향이므로 D3PM에서는 아래 수식으로 p{\theta}를 정의

    • 1단계 denoising 과정 = 개별 토큰 위치에 대한 denoise는 독립 과정 = x^\ell 근사

    • x^{\ell} (원본 텍스트)가 주어진다면 q를 활용해 x_t^\ell \rightarrow x_s^\ell을 완전히 복구할 수 있음.

    • denoise 과정에서 x^\ell이 주어지지 않으므로 p로 근사: p_\theta\left(\mathbf{x}^{\ell} \mid \mathbf{x}_t\right)

  • Negative ELBO (NELBO)를 이용해 학습

  • 1, 2항: noise, denoise 과정에서의 샘플의 일치 정도

  • 3항 얼마나 noise를 잘 만들었는가

BLOCK DIFFUSION LANGUAGE MODELING

BLOCK DIFFUSION DISTRIBUTIONS AND MODEL ARCHITECTURES

Block Definition

  • 길이 L’이 되게 B개의 block으로 만들기 (x^b: x^{(b-1)L’:bL’} \in {1,…,B})

  • Likelihood over block

block 내에서 reverse diffusion 프로세스 적용

  • block이 constraint인 것을 제외하면 preliminaries의 수식과 동일!

Learning Objective

NELBO를 적용해 위와 같이 학습 목적함수 정의, 이것도 Sum을 제외하곤 전부 같음!

Denoiser model

  • Transformer x\theta를 사용해 파라미터화: p\theta(x^b x_t^b, x^{<b})

    • given x^{<b}: AR 특성 유지

    • x^b 예측: Denosing

  • Block들에 대해 병렬적 학습을 가능하게 함 (block-causal attention mask)

  • x\theta의 학습: block b 내에서 x\theta^b(x_t^b, x^{<b}) → L’ 길이의 결과 예측

→ 아래 K, V 캐시 수식을 보시면 모델을 이해하기 쉬움!

K, V caching

  • recomputing을 막기 위한 block 단위 caching

EFFICIENT TRAINING AND SAMPLING ALGORITHMS

Training

  • 모든 block은 x_\theta의 forward pass를 두 번 거쳐야 함 (x_t^b, x^b) → 계산의 효율화 필요

  1. Block 별로 noise level sampling

  2. 각 block에 대해 noisy input x_{t_b}^b 생성

  3. \left(\emptyset, \mathbf{K}^{1: B}, \mathbf{V}^{1: B}\right) \leftarrow \mathbf{x}_\theta(\mathbf{x}): 원본 x를 이용해 K, V cache 미리 다 계산하기

  4. 모든 b에 대해 x^b_{\text{logit}} 계산

  • Naive: B-times loop를 이용해 forward pass를 별도로 진행

  • Vectorized 방식

    • x{\text {noisy }}=x{t1}^1 \oplus x{t2}^2 \oplus \cdots \oplus x{t_B}^B

    • x_{\text{noisy}} \oplus x을 input으로 하여 한 번에 계산 How? attention mask를 이전 block만 조회하게끔 조절

Sampling

  • Block 단위의 순차적 샘플링, K, V 캐싱 가능 ← AR의 장점

  • arbitrary length 생성 가능 ← AR의 장점

  • block 내부에선 Parallel하게 생성 가능 ← Diffusion의 장점

UNDERSTANDING LIKELIHOOD GAPS BETWEEN DIFFUSION & AR MODELS

MASKED BD3-LMS

  • 최근 가장 큰 효과를 보이고 있는 masking noise process를 적용

  • Per-token noise process

    • \alpha_0=1 → linear scheduler→ \alpha_1=0

  • 목적 함수 (Sahoo et al. (2024b)의 SUBS-parameterization denoising 모델 철학을 따름!!)

    • Zero Masking Probabilities: clean sequence( x^\ell)에는 mask를 포함하지 않음. (이건 아래의 조건을 위해 필요한듯합니다.)

    • Carry-Over Unmasking: x_t^\ell \neq m인 경우 q\left(x_s^l=x_t^l \mid x_t^l \neq m\right)=1. 즉, unmaksed된 token은 다시 mask 되지 않음.

      • Denoising model 단순화: p_\theta\left(x_s^{\ell}=x_t^{\ell} \mid x_t^{\ell} \neq m\right)=1

    • \alphat = \prod{\tau=1}^{t}(1 - \beta_\tau): t시점까지 mask되지 않고 살아남을 확률

    • why?

      • t 시점에서 mask transition matrix (noising 과정에서 i→ j로 변환)

        • 순서대로 mask는 mask 유지

        • 값을 그대로 가질 확률: \alpha_t

        • token이 mask 될 확률: 1 - \alpha_t

      • marginal Q*{t s} (여기서 \alpha*{t s} = \alpha_t/\alpha_s)

전개…… \mathcal{L}_{\text{diffusion}}은 앞의 수식과 의미적으로 같습니다…..

- 일단 여기까진 정의대로 가되 block 내 token 길이인 L'으로 확장

- KL divergence 정의에 의해 다음과 같이 전개 가능 (이건 ㄹㅇ KLD 정의)

- \log{q} 부분은 학습과 무관하므로 제외

  - q(x_s^{b,\ell} = x^{b,\ell} | x_t^{b,\ell} = m, x^{b,\ell}) = \frac{\alpha_s - \alpha_t}{1 - \alpha_t}

  - q(x_s^{b,\ell} = m | x_t^{b,\ell} = m, x^{b,\ell}) = \frac{1 - \alpha_s}{1 - \alpha_t}

  - q(x_s^{b,\ell} = x^{b,\ell} | x_t^{b,\ell} = x^{b,\ell}, x^{b,\ell}) = 1: 1이므로 뒤에 계산에서 제외

- x_t^{b,\ell}이 mask인 경우만 계산

- 뒤에 항은 mask → mask는 상수라서 계산에서 제외
= \sum{b=1}^{B} \mathbb{E}_t \mathbb{E}_q T \left[ \sum{\ell=1}^{L’} \frac{\alphat - \alpha_s}{1 - \alpha_t} \log p\theta(x^{b,\ell} x_t^{b,\ell}, x^{<b}) \right]
= \sum{b=1}^{B} \mathbb{E}_t \mathbb{E}_q T \left[ \frac{\alpha_t - \alpha_s}{1 - \alpha_t} \log p\theta(x^b x_t^b, x^{<b}) \right]

T \rarr \infin, T(\alpha_t - \alpha_s) = \alpha’_t

CASE STUDY: SINGLE TOKEN GENERATION

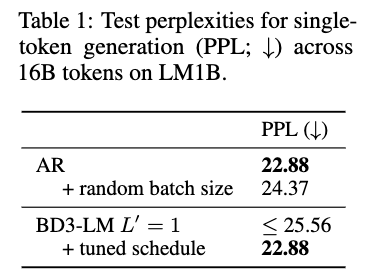
  • L^\prime = 1인 경우, MASKED BD3-LMS의 목적함수는 autoregressive NLL과 동등함.

    • 직관적 핵석: block의 길이가 1이라면 한 토큰 단위 AR과 같음. → ??? 그래도 한 토큰 단위로 일어나는 diffusion 과정이 있는데? → mask로 intitialize 후, 원하는 다음 token을 찾는 과정이란 점에선 동일.

    • **수식 ok**

      • linear scheduler에서 \alpha’_t, \alpha_t의 정의는 위와 같음. 그 다음 전개 과정은 이해할 수 있을듯?

      • Expanding 부분은 Expatation of q를 제거 하기 위한 과정 q가 mask transition을 전제로 하므로 경우 (mask/unmask) 두 가지 확률에 대해서 전개

      • SUBS-parameterization 가정의 carry-over unmasking 특성으로 \log{p_\theta(x^b x_t^b=x^b, x^{<b})} = 0
        • q(x_t^b=m x^b) = 1 - \alpha_t = 1 - (1 - t) = t

        • t는 상관없으니깐 삭제!

        • 최종 결과는 NLL 로스와 기대값이 같다!

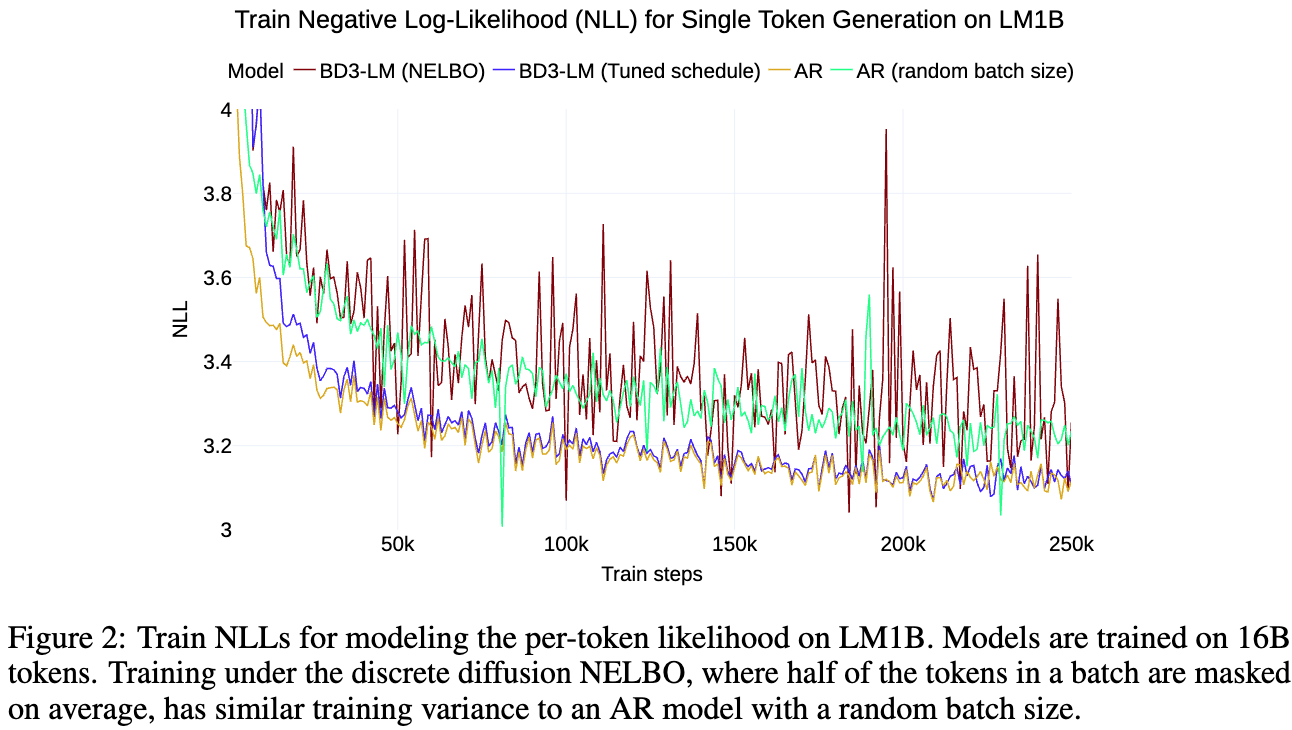
  • 학습 목표의 기대값이 같음에도 불구하고 perplexity gap (=높은 학습 variance)가 존재함을 확인

  • 왜 그럴까? \mathbb{E}_{t\sim\mathcal{U}[0,1]}q(x_t^\ell=m x^\ell) = 0.5 기본적으로 학습에 사용하는 token의 수가 절반으로 줄기 때문에 variance가 커지는 것
  • tuned schedule: q(x_t^\ell = m x^\ell) = 1

    • 해당 schedule에서는 AR의 목적함수와 완전히 동일

    • PPL도 감소, NELBO의 분산도 감소

DIFFUSION GAP FROM HIGH VARIANCE TRAINING

  • Case study를 넘어 L^\ell \geq 1인 케이스로 확장하고 싶음!

    • NELBO는 이론적으로 t에 invariance (기존 연구 ref: T가 무한히 커질수록 \alpha값이 아닌 누적값에 의해서 기대값이 정의되기 때문… 이 이상의 이해는 포기)하기에 스케줄에 따른 기대값의 변화가 없어야 함.

    • 하지만 우리는 모든 연산을 한 번에 하는 것이 아닌 Batch 연산을 활용 → 이론적인 invariance가 깨짐

→ Schedule에 따라 분산의 결과가 변하게 됨. → Schedule을 잘 만들어보자!

  • Batch size를 K라고 할 때, batch of sequence \text{X} = [x^{(1)},x^{(1)},…,x^{(K)}], with each \text{x}^{(k)} \overset{\text{iid}}{\sim} q(x)

  • NELBO estimator

  • Variance of the gradient estimator

LOW-VARIANCE NOISE SCHEDULES FOR BD3-LMS

INTUITION: AVOID EXTREME MASK RATES & CLIPPED SCHEDULES FOR LOW-VARIANCE GRADIENTS

  • 이상적인 마스킹: 모델이 다양한 수준의 노이즈 [MASK]에서 원래대로 되돌리는 법을 배우는 것

  • 극단적인 마스킹

    • 마스킹 토큰이 너무 적을 경우, 너무 쉬운 문제를 풀게 됨.

    • 모든 토큰이 마스킹 될 경우, 문맥 정보가 전혀 없음 빈도에 기반한 학습만 진행

→ 극단적인 부분을 날린 CLIP을 이용하자

→ sample mask rates: 1 - \alpha_t \sim \mathcal{U}[\beta, \omega] for 0 \leq \beta, \omega \leq 1

DATA-DRIVEN CLIPPED SCHEDULES ACROSS BLOCK SIZES

  • Block size ( L’)에 따른 최적의 mask rate을 찾아보자.

  • Gradient 분산을 최소화하기 위함이지만 아래 NELBO를 추정지로 하여 실험을 진행

    • forward pass만으로 계산 가능

    • 실험 결과들에서 NELBO와 기울기 분산이 같은 경향성을 보임을 확인

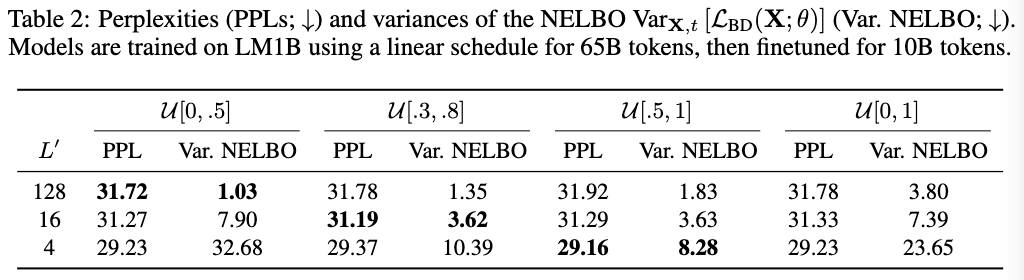
  • \beta, \omega에 대해 grid search 진행

  • Table 2에서 PPL과 NELBO과 상관성 보임을 재차 확인 + L’에 따라 최적의 조합이 있음을 발견함.

EXPERIMENTS

  • Pre-train: base BD3-LM ( L’=L) for 850K gradient steps (순수 diffusion?)

  • Fine-tune

    • 150K gradient steps on One Billion Words dataset (LM1B) and OpenWebText (OWT)

  • L’에 따라 다른 Clipped schedule 적용 (매 validation epoch 마다 최적의 \beta, \omega 조합을 찾음!)

LIKELIHOOD EVALUATION

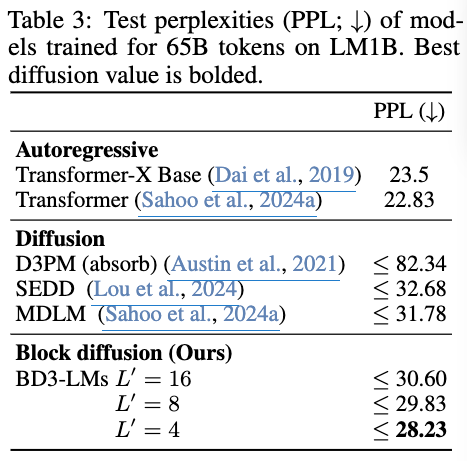
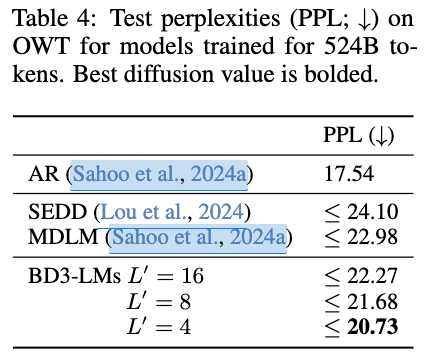
  • 다른 MDLM 모델 대비 perplexity이 향상됨

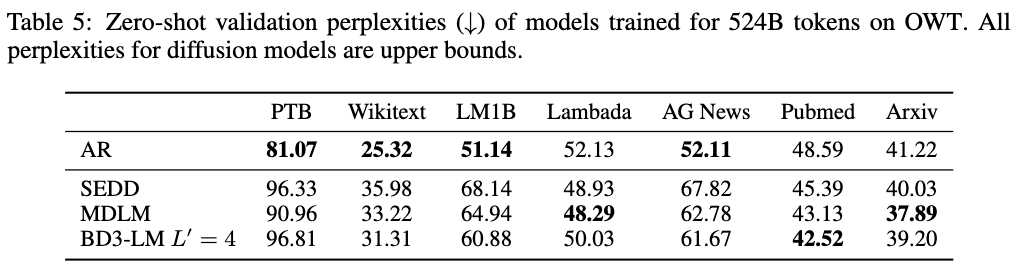
  • Zero-shot validation perplexity 결과 Pubmed는 AR보다도 잘함.

  • 대체로 다른 MDLM보단 PPL 값이 더 낮음.

SAMPLE QUALITY AND VARIABLE-LENGTH SEQUENCE GENERATION

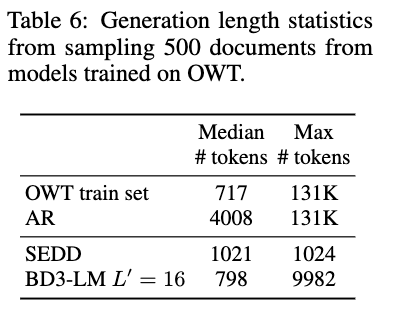
  • [EOS] 토큰을 생성하거나 sample quality가 급감 (the average entropy of the the last 256-token chunk is below 4)할 때까지 실험 진행

  • SEDD 대비 최대 10배 더 긴 text 생성 가능함.

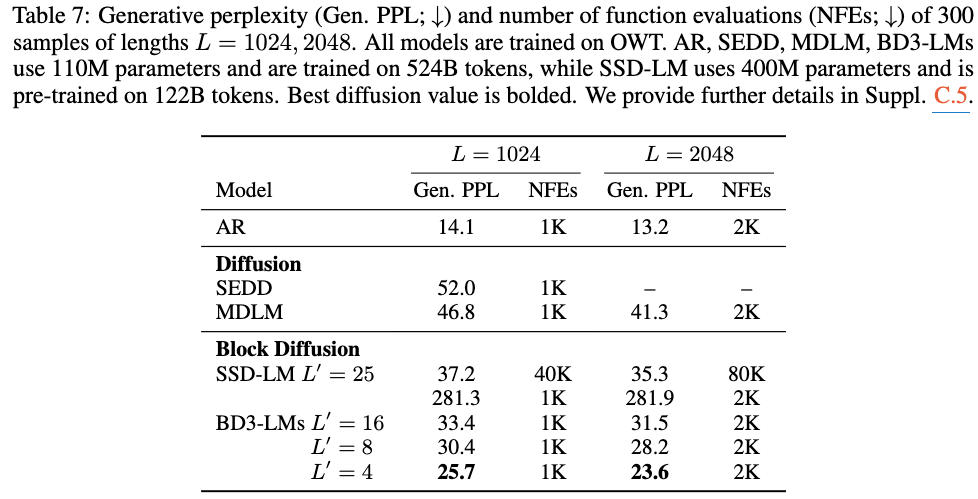
  • GPT-2를 이용해 generative perplexity 측정, 효율성을 보기 위해 the number of generation steps (NFEs)

  • 기존 Block Diffusion 대비해도 더 적은 step에서 높은 Gen PPL 달성

  • 정성 분석은 Appendix D에 있음. AR과 유사할 정도의 퀄리티, 다른 DLM보단 좋더라

ABLATIONS

SELECTING NOISE SCHEDULES TO REDUCE TRAINING VARIANCE

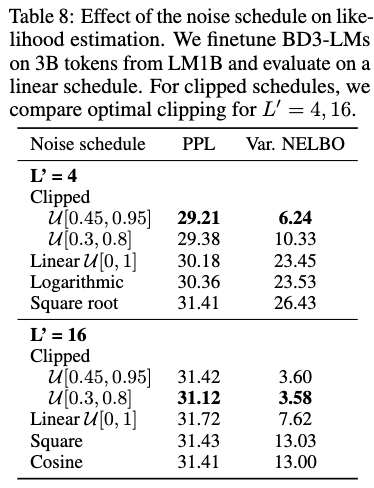
  • L’이 작을수록 heavier mask가 효과적

EFFICIENCY OF TRAINING ALGORITHM

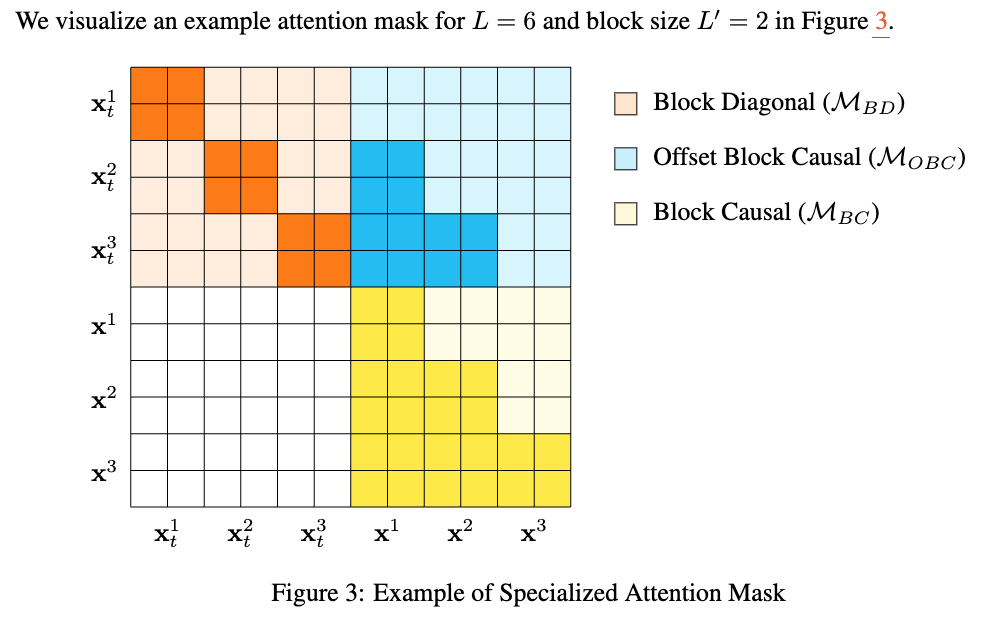
  • concat 활용하여 처리할 경우, sparse attention mask 활용

  • FlexAttention을 이용할 경우 Sparsity를 활용해 효율적 처리 가능

  • 20-25% 속도 향상 가능!

  • 수학 공부 열심히 하자.

  • 결과에서 힘이 많이 빠지긴 한다.

  • 전개과정에서 이 정도는 해야 oral로 가는구나 벽느껴진다.