논문 정보

Date: 2025-01-02
Reviewer: 김재희
Property: DiffusionLM, Pre-training

masked diffusion language model의 수학적 기초를 다진 논문에 대해 살펴보겠습니다.

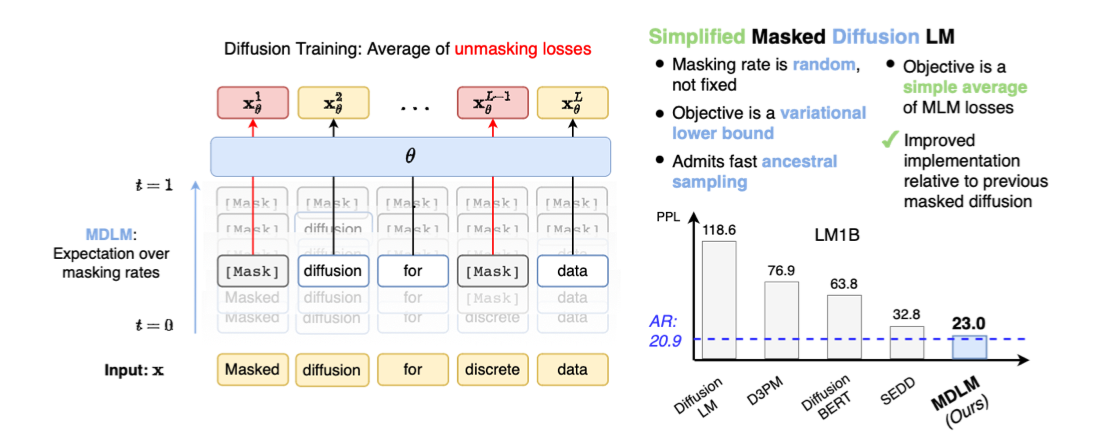
Preliminary

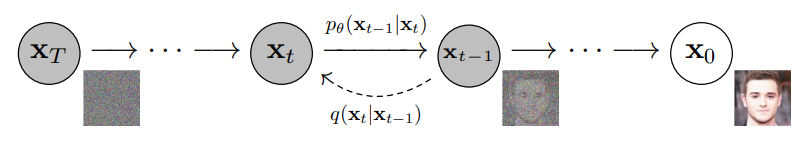
Forward process: 원본 데이터에 대해 일정 비율의 노이즈를 입력하여 훼손하는 과정
- 최대 T번 반복
- scherduler: step t에서 유지할 정보의 수준을 정함 or 입력할 노이즈의 수준
- prior: 노이즈가 샘플링되는 분포 or 생성 시 가장 첫 시점(t=T)의 데이터 분포
Backward process: t번 훼손된 데이터에 대하여 s번 훼손된 데이터로 복원하는 과정 (t > s)
- 실제 모델의 학습 대상 → 완전한 노이즈 데이터에서 실제 데이터를 생성(샘플링) 할 수 있게 됨
training objective function

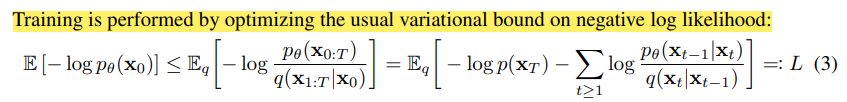
원래 objective function(- \log p_{\theta}(x_0))은 필요한 계산이 너무 많음
- 완전한 노이즈(x_T)부터 T개의 모든 스텝에 대해 1) 노이즈를 가하고 2) 모델을 통해 복원하는 과정을 수행해야 함

⇒ 매우 연산량/메모리를 많이 차지하게 됨

원 목적함수의 ELBo를 변분추론(몰라요…)을 통해 산출하게 됨
- Expectation 항으로 구성되기 때문에 모든 step 계산이 필요 없어짐

- x_0: 실제 데이터(그냥 배치로 가져오는 과정)

- t: uniform dist에서 샘플링 (매 데이터마다 하나의 step에 대해서만 학습 진행) ⇒ 원 목적함수 대비 연산량이 매우 줄어들게 됨.

- \eta: 실제 noise, 매 iter마다 다른 noise를 주입해야 하므로 새로 sampling

실제로는 stepwise denoising term만을 사용하여 학습이 진행되게 됨
- 실제로 t-1 → t step에서 가해진 noise를 모델이 예측하도록 학습됨.

Diffusion Model의 주된 연구 분야인 이미지는 continuous한 변수(pixel)을 다루기 때문에 모든 변수 및 과정이 이를 기반으로 진행됨.

MDLM(Masked Diffusion Language Model)

텍스트 도메인에 적절한 diffusion modeling은 무엇일까?

텍스트 도메인의 특징 (뇌피셜)

text: 매우 고밀도의 정보가 보존된 도메인. 이미지와 다르게 정보량이 거의 없는 변수가 적음

⇒ embedding에 가하는 노이즈는 크기가 매우 작더라도 큰 의미변화를 만들어낼 수 있음

discrete: 단어는 존재하거나, 존재하지 않는 binary한 변수임
continuous한 noise를 삽입하는 interpolation이 불가능함
embedding을 이용한 diffusion 방법론이 있지만 아직까지는 MDLM이 더 나은 방법론으로 보임

수식 전개 Discrete Diffusion

\textit{V} = [사과, 존맛탱, mask]

입력문장: 사과 존맛탱

forward process: 노이즈를 주입, actual token → mask

q\left(\mathbf{z}_t \mid \mathbf{x}\right)=\operatorname{Cat}\left(\mathbf{z}_t ; \alpha_t \mathbf{x}+\left(1-\alpha_t\right) \boldsymbol{\pi}\right)

Terms
- x: 원본 텍스트(1-hot encoding), [1, 0, 0]
- \alpha_t: t 시점의 원본 텍스트 보존 비율, 1-\alpha_t: masking token 비율, scheduler를 통해 결정됨

(\alphat < \alpha{t-1})

\pi: noise 분포, MDLM에서는 그냥 mask 토큰을 noise로 사용하므로 mask 토큰의 인덱스만 1인 1-hot vector로 볼 수 있음 [0,0,1]
설명
1. q(\textbf{z}_t \textbf{x}): 원본 텍스트(x)에서 t step의 훼손된 텍스트(\textbf{z}_t) 가 산출될 확률 [0.7, 0, 0.3]
2. \alpha_t\textbf{x}: 원본 텍스트가 보존될 확률, [0.7, 0, 0]
3. (1-\alpha_t)\pi: 마스크 토큰으로 전환될 확률 [0, 0, 0.3]

⇒ 매 시점마다 점차 많은 토큰들이 mask 토큰으로 전환됨

reverse posterior: 노이즈를 복원, mask → actual token

reverse posterior

q\left(\mathbf{z}s \mid \mathbf{z}_t, \mathbf{x}\right)=\operatorname{Cat}\left(\mathbf{z}_s ;\frac{\left[\alpha{t \mid s} \mathbf{z}t+\left(1-\alpha{t \mid s}\right) \mathbf{1} \boldsymbol{\pi}^{\top} \mathbf{z}_t\right] \odot\left[\alpha_s \mathbf{x}+\left(1-\alpha_s\right) \boldsymbol{\pi}\right]}{\alpha_t \mathbf{z}_t^{\top} \mathbf{x}+\left(1-\alpha_t\right) \mathbf{z}_t^{\top} \boldsymbol{\pi}}\right)

t step에서 이전 시점 s(<t)까지 노이즈를 복원하기 위한 추정 확률
- 어떤 토큰이 masking되었는지 알 수 없으므로 확률적으로 추정해야 함
- 0<\alpha_{t s} = \frac{\alpha_t}{\alpha_s}<1: s step과 t step 사이에서 보존되는 원본 토큰 비율
  - length: 100
  - s(70) → t(50)
  - \textbf{a}_{t s} = \frac{0.5}{0.7}=\frac{5}{7}
- \alpha{t \mid s} \mathbf{z}_t+\left(1-\alpha{t \mid s}\right) \mathbf{1} \boldsymbol{\pi}^{\top}\textbf{z}^t: s step과 t step 사이에서 보존되었던 원본 토큰 확률(\alpha_{t \mid s} \mathbf{z}_t)과 masking으로 변해버렸던 토큰의 확률(\mathbf{1} \boldsymbol{\pi}^{\top} \mathbf{z}_t)
  - s step에서 t step으로 진행되면서 masking된 토큰을 추정하는 항
  - 어떤 토큰을 복원할지 정하는 항
  - [0.7, 0.7, 0.7] [1, 0, 0] + [0.3, 0.3, 0.3] [1,1,1][1,0,0]
    - [0.7, 0, 0] + [0, 0., 0.3] = [0.7, 0, 0.3]
- \alpha_s\textbf{x} + (1-\alpha_s) \boldsymbol{\pi}: 원본 토큰(\textbf{x})의 확률과 masking 토큰으로 처리될 확률(\pi)
  - s step에서는 \alpha_s 비율의 토큰만 원본 토큰이어야 하고, (1-\alpha_s) 는 마스크 토큰이어야 하므로 1) 어떤 위치를 원본 토큰으로 남길지 2) 해당 위치에 어떤 토큰으로 복원할지 정하는 항임

사실 지금까지의 수식은 masked diffusion은 아닙니다. 지금까지의 수식은 아래와 같은 특성을 가정하고 전개되었습니다.

discrete한 time step
\pi의 noise distribution이 존재

하지만 masked diffusion은 이를 좀 더 단순화해서 사용할 수 있습니다. 왜냐하면 \pi=m이기 때문입니다.

⇒ 노이즈는 임의의 분포가 아니라 무조건 masking token이다! 그러므로 이전 step에서 masking된 토큰은 이후에도 무조건 masking되어 존재하게 된다!

Masked Diffusion

forward masking process

q\left(\mathbf{z}_t \mid \mathbf{x}\right)=\operatorname{Cat}\left(\mathbf{z}_t ; \alpha_t \mathbf{x}+\left(1-\alpha_t\right) \boldsymbol{m}\right)

discrete diffusion에서 \pi가 m으로 변한 것 외에 차이 없습니다.

reverse posterior: 실제 loss 식을 산출하기 위해 필요한 항

q\left(\mathbf{z}_s \mid \mathbf{z}_t, \mathbf{x}\right)= \begin{cases}\operatorname{Cat}\left(\mathbf{z}_s ; \mathbf{z}_t\right) & \mathbf{z}_t \neq \mathbf{m} \ \operatorname{Cat}\left(\mathbf{z}_s ; \frac{\left(1-\alpha_s\right) \mathbf{m}+\left(\alpha_s-\alpha_t\right) \mathbf{x}}{1-\alpha_t}\right) & \mathbf{z}_t=\mathbf{m}\end{cases}

\textbf{z}_t \neq \textbf{m}: step t에서 원본토큰이라면 → 그대로 유지
\textbf{z} = \textbf{m}: step t에서 masking token이라면 → step s에서 t 사이에서 masking되었을 확률 산출
- 근데 실제 텍스트(\textbf{x})를 알아야 산출할 수 있는 항

⇒ 복원 단계에서는 알 수 없으니 MDLM이 등장

⇒ \textbf{x}_\theta(\textbf{z}_t, t): \theta를 파라미터로 가지는 모델에 의해 t step에서 복원된 문장

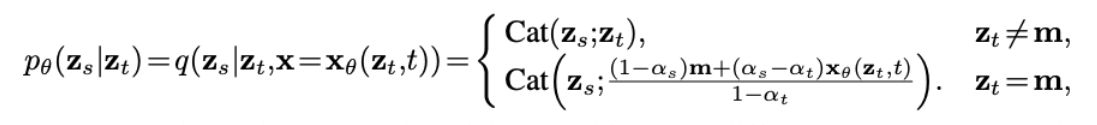
MDLM의 상황에 맞춘 2가지 property

Zero Masking Probabilities: <\textbf{x}, \textbf{m}>=0임. 즉, 원본 토큰 중에는 masking token이 사용되지 않음

⇒ 모델을 통해 복원할 때, mask token에 대한 logit은 -\infin로 처리

Carry-Over Unmasking: step t에서 복원(unmasking)된 토큰은 이후 모델의 복원 과정에서 수정되지 않음
t=4에서 “a”라고 복원되었다면, t=1에서 “b”로 바뀌지 않고 무조건 “a”로 고정

Rao-Balckwellized Likelihood Bounds

diffusion loss를 산출하듯이 본래 학습할 discrete-time diffusion의 loss의 lower bound를 산출하면 아래와 같음

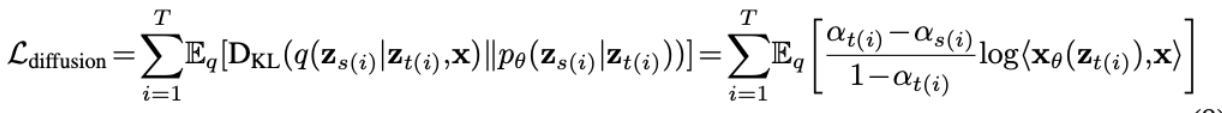
Continuous-Time Likelihood Bounds

기존 연구에서 정리하기로 T \to \infin로 정의할 경우 더욱 tight한 lower bound를 산출할 수 있음

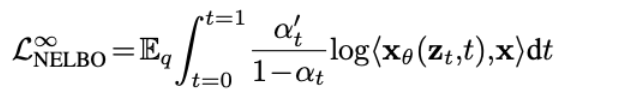
Masked Diffusion Language Models

앞에서 정의된 tight한 lower bound를 language modeling 상황으로 가져오기 위해 아래 가정들을 적용할 수 있음

\textbf{x}^{1:L}: L개의 token sequence
\textbf{x}^\textit{l}: \textit{l}번째 토큰
forward와 backward 모두 각 토큰들이 독립적으로 진행

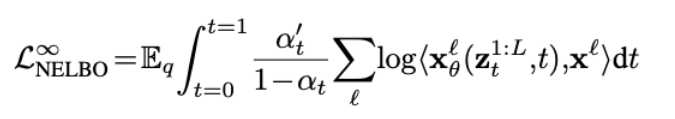
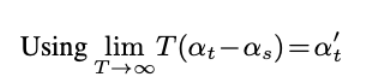
\textbf{x}^\textit{l}_\theta(\textbf{z}_t^{1:L}, t): t번째 step에서의 시퀀스에 대한 모델의 예측 문장, masking된 토큰을 예측하여 복원한 문장문
\log<\textbf{x}^\textit{l}_\theta(\textbf{z}_t^{1:L}, t), \textbf{x}^\textit{l}>: loglikelihood, 갑자기요…?!
이때 \alpha_s 가 사라진 것을 확인할 수 있음
- masking과 unmasking 시 scheduler의 필요성 X → 많은 연산을 생략할 수 있음, 추론 시 이점 존재
- 실제 masking 비율에 따라 다른 loss 반영
  - 많은 토큰이 masking된 경우(\alpha_t가 작은 경우): weight가 작아짐 ⇒ 모델이 불확실할 수 밖에 없는 상황에서 학습을 적게 반영
  - 적은 토큰이 masking된 경우(\alpha_t가 큰 경우): weight가 커짐 ⇒ 모델이 확실히 맞추어야 하는 데이터에 대해 학습을 많이 반영

MDLM은 결국 discrete-time diffusion model을 masking과 text domain에 적합한 가정을 도입한 결과 weighted sum of MLM이라는 결론에 도달

BERT의 목적함수를 일부 변형하는 것으로 도입이 가능해짐!

Training Algorithm

데이터 sampling
step sampling
이전 step 대비 추가적으로 \alpha_t 비율을 masking한 masked input 산출
weighted sum of MLM loss 형식으로 update

Actual Inference

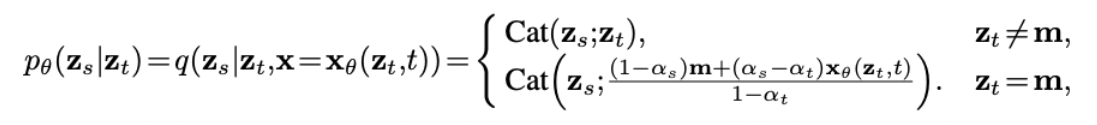
해당 수식을 통해 실제 생성이 이루어지게 됨

\textbf{z}_t = \textbf{m}: t step에서 mask 토큰으로 입력된 위치에 대해서만 예측 수행

\frac{(1-\alphas)\textbf{m} + (\alpha_s - \alpha_t)\textbf{x}\theta(\textbf{z}t, t)}{1-\alpha_t} = \frac{1-\alpha_s}{1-\alpha_t}\textbf{m} + \frac{\alpha_s-\alpha_t}{1-\alpha_t}\textbf{x}\theta(\textbf{z}_t, t): 모든 mask 토큰 위치에서 예측된 확률분포 중에서 \frac{1-\alpha_s}{1-\alpha_t} 비율은 다시 masking으로 돌림

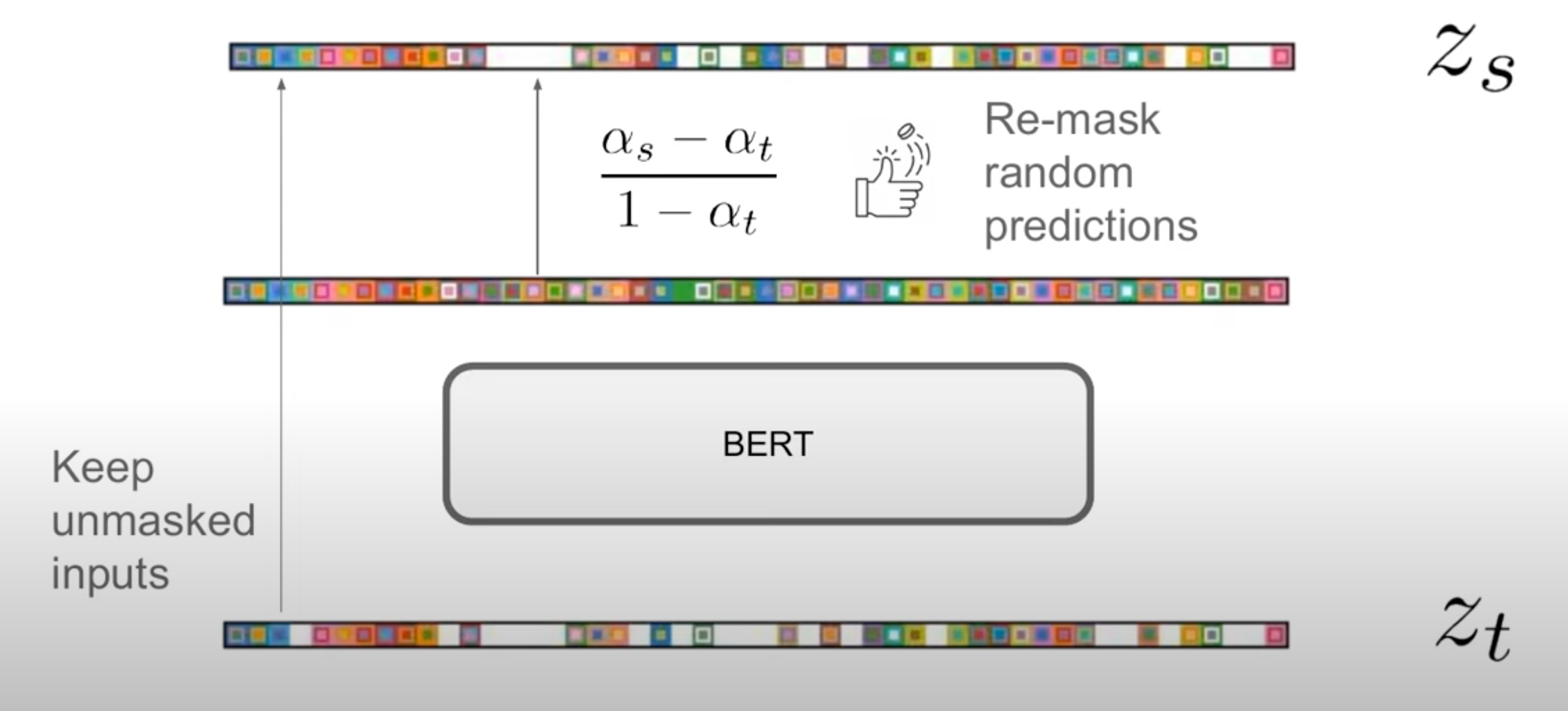
⇒ 매 iteration 마다 \frac{\alpha_s - \alpha_t}{1-\alpha_t}만큼의 토큰이 복원되면서 생성

Experiments

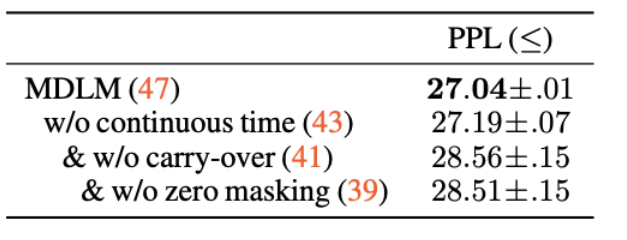
1. Perplexity evaluation

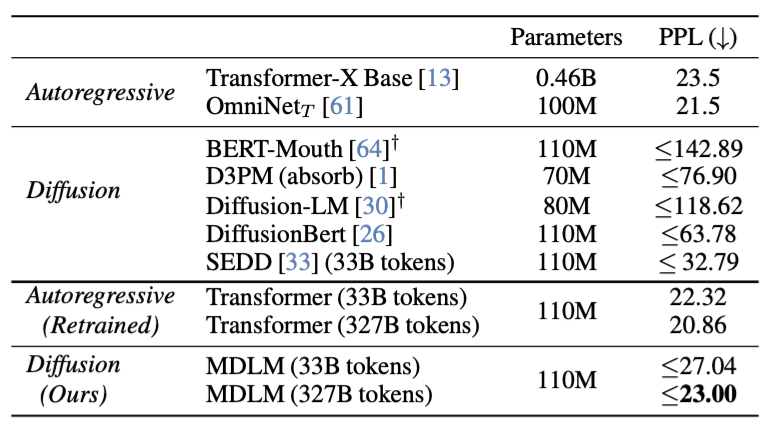
동일한 corpus를 이용하여 autoregressive model과 MDLM을 학습시켜 비교

⇒ 실제 입력되는 non-masked token 수의 차이를 없애기 위한 다른 update step 사용

autoregressive model: 0.5M step
MDLM: 1M step

2. Training NLL

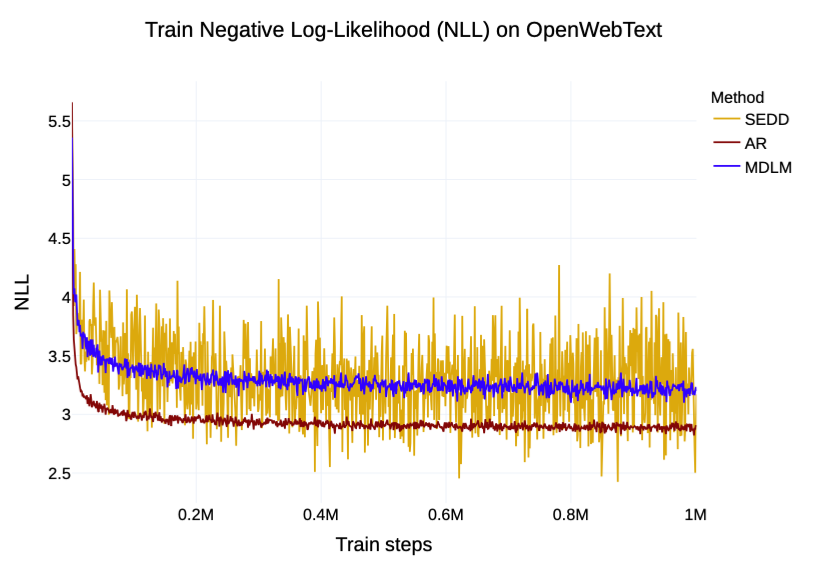
기존 DDLM(SEDD)보다 훨씬 안정적인 NLL을 보이며 학습

⇒ 2가지 property를 이용하여 tight한 lower bound를 형성한 덕분

3. Zero-shot Perplexity

다양한 분야에 대하여 AR과 근접한 수준의 성능 달성
- PubMed, Arxiv와 같은 특수 도메인의 경우에는 DDLM이 AR보다 나은 모습을 보임 → Unmasking 학습 방식 자체가 OOD에 robust할 수 있음

4. Downstream Task

BERT를 MDLM으로 일부 finetune한 결과로 비교
- 5k step finetune 진행
- 사실 큰 의미는 모르겠음…

conclusion

수식 전개를 통해서 weighted sum of MLM 형식의 diffusion model formulation
기존 diffuion lm들보다 좋은 성능과 안정된 학습을 보임
- (여기서 다루지는 않았지만) 간단한 추론 caching 및 생성 방법론도 함께 제시하여 후속 연구로 이어짐
해당 논문의 프레임워크가 이후 LLaDA 등에서 활용 ⇒ 아마 향후 MDLM의 표준이 되지 않을까…?