Logic-RL: Unleashing LLM Reasoning with Rule-Based Reinforcement Learning

논문 정보

• Date: 2025-03-04
• Reviewer: 전민진
• Property: RL

Deepseek-R1에서 사용한 rule-based reinforcement learning을 작은 모델에 대해 적용해 다양하게 실험한 논문

⇒ rule-based reinforcement learning 꿀팁 전수

Abstract

• DeepSeek-R1의 성공에서 영감을 받아서 rule-based reinforcement learning이 large reasoning model(7B)에 미치는 영향을 분석

• synthetic logic puzzle을 training data로 활용해 분석 실험

  • 난이도 조절이 용이하고, answer verification이 직관적

• 실험 결과, 효과적이고 안정적인 RL학습을 위한 기술적 꿀팁을 소개

  • thinking, answering process를 강조하는 system prompt사용, 엄격한 format reward function, 직관적인 학습 레시피 등

• 7B모델을 rule-based RL을 통해서 reflection, verification, summarization과 같은 reasoning skill을 학습할 수 있었음

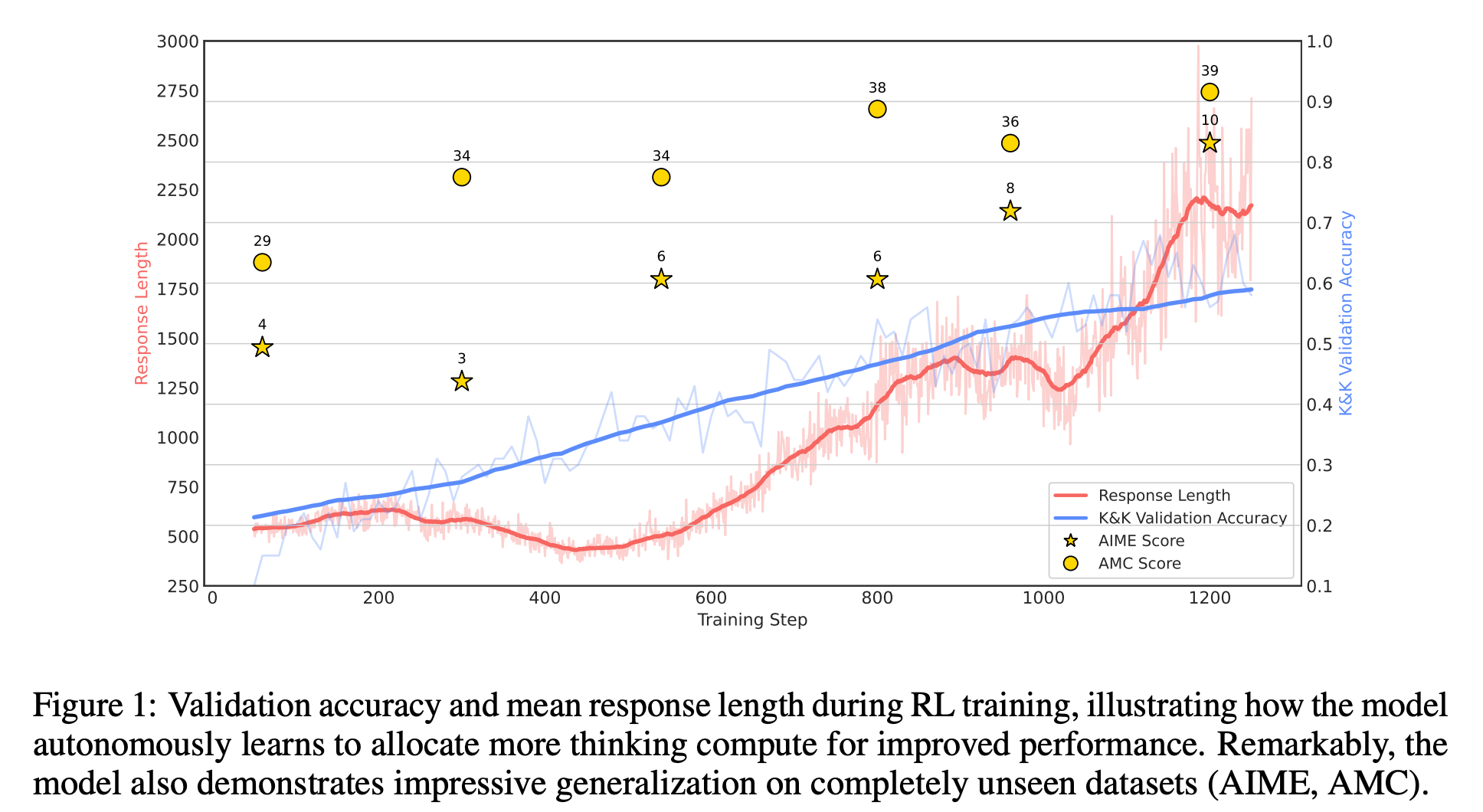
  • 특히 5K개의 logic problem로 학습한 후에 수학 데이터셋인 AIME와 AMC에 대한 일반화 성능도 좋았음

Introduction

• LLM의 post-training은 DeepSeek-R1, Kimi-K 1.5, OpenAI-o1과 함께 급속도로 발전

• 특히 DeepSeek-R1의 경우 기존의 핵심 기법인 Monte Carlo Tree Search(MCTS), Process Reward Models(PRM)을 사용하지 않고, 간단하면서 효과적인 rule-based reinforcement learning을 소개

  • 하지만 이 친구들은 큰 모델(>600B)에 대해서만 학습 진행, 모델은 공개했지만 학습 데이터는 공개하지 않음

⇒ 작은 모델에도 이러한 방식의 학습이 효과적인가에 대한 탐구 부족

1. 작은 모델에서도 이러한 reasoning ability가 발생할 것인가, 2. 이런 능력을 기르기 위해 최적의 학습 데이터 구조는 무엇인가, 3. 어떤 방식이 이러한 결과를 똑같이 보여줄 수 있는가 등

• 이러한 질문에 대해 답을 하기 위해 실험에 사용하는 데이터가 controllable해야함 ⇒ Knights and Knaves (K&K) logic puzzle dataset를 학습 데이터로 사용

  • GSM8K나 Omini-MATH는 학습 데이터의 난이도를 조절하기가 어려움

  • 하지만 퍼즐 데이터는 난이도 조절도 쉽고, 답 검증하기도 쉬움

• 본 논문에서는 Logic-RL, R1과 같은 reasoning pattern을 logic puzzle 학습으로 얻는 rule-based reinforcement learning framework를 소개

  • (이 논문은 방법론 보다는 그냥 테크니컬 리포트 느낌)

  • 학습 프레임워크에서는 REINFORCE++ algorithm을 사용하고, DeepSeek-R1과 같은 reward 디자인을 차용

  • 얘네가 제안한거는 practical system prompt와 엄격한 format reward.. 와 REINFORCE++ algorithm의 수정 버전

• 5000개의 로직 퍼즐로 학습했을 때, 로직퍼즐에 대한 성능 뿐만 아니라 cross-domain generalization 성능도 높아짐

⇒ RL로 학습된 reasoning heuristics은 abstract problem-solving schemata를 발달시킴!

• 실험을 하면서 얻은 여러 인사이트

  • 긴 답변이 나은 reasoning을 보장하지 않는다

  • 언어가 섞이면 reasoning을 지연시킨다

  • ‘thinking’ token의 증가는 도움이 된다

  • SFT는 암기고, RL은 일반화다

  • Cold start는 보너스지 필수는 아니다

  • Curriculum learning이 중요하다

Method

Data Synthesis

• Knights and Knaves (K&K) puzzle은 추리? 느낌의 퀴즈

  • 등장인물은 항상 사실만을 말하는 기사와 항상 거짓만을 말하는 악당, 둘 중 하나임

  • 이 데이터셋은 컨트롤하기가 아주 좋음

1. Procedural Generation : 퍼즐은 logic template를 사용해서 생성됨 ⇒ consistency와 무한한 variability를 보장

2. Controlled Difficulty Levels : 퍼즐의 난이도는 등장인물의 수와, logical operation(1-4 combination of Boolean operators)으로 조절 가능

3. 더 복잡한 퍼즐은 OOD test느낌으로 활용 가능

4. Ease of Verification : 각 퍼즐은 하나의 명확한 답이 있음

Rule Based Reward Modeling

• reward은 학습에 필요한 핵심 시그널

• 하지만 저자들은 모델의 output에서 hacking behavior를 관찰했고, reward design을 계속 바꿈 ⇒ 아래가 이제 거의 unhackable한 rule-based reward system.

  • Format reward와 Answer Reward로 구성되어 있음

• Format Reward

  • think는 사이에, answer은 사이에 있도록 강제

  • 추가로, tag는 prompt의 끝 부분에 포함하는 것을 추천한다고 함

    • 그래서 모델이 instruction following하기가 용이

  • 완벽하지 않은 룰 디자인일 때, 계속 모델의 reward hacking현상을 관찰했는데, 아래와 같음

• 따라서, 반복적으로 룰을 수정 ⇒ 각 태그가 정확히 한번만 나타나게 한다거나, thinking process는 반드시 reasoning안에 포함되도록 하거나, 결론이 extractable and readable manner로 제공되도록 함

• format score는 포맷이 맞으면 1, 틀리면 -1로 계산

• Answer Reward

  • 답변을 평가하는 파트, 모델의 답변이 얼마나 정답과 일치하는지를 평가

RL Algorithm

• Reinforce Return Calculation

  • 각 trajectory에 대한 discounted cumulative reward를 아래와 같이 계산, 본 논문에서는 감마 1로 사용

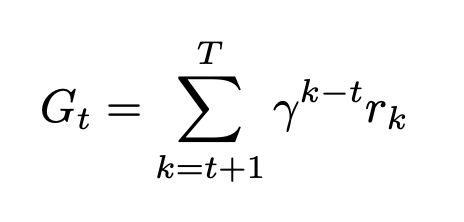
⇒ 아래는 DeepSeek-Math의 추천에 따라, REINFORCE++를 구현할 때 몇가지 수정사항을 반영

• First modification : Use KL Loss

  • PPO의 reward function에는 KL divergence loss가 포함됨.

    • 토큰별로 reward는 다음과 같이 정의됨 (EOS 토큰까지만 계산)

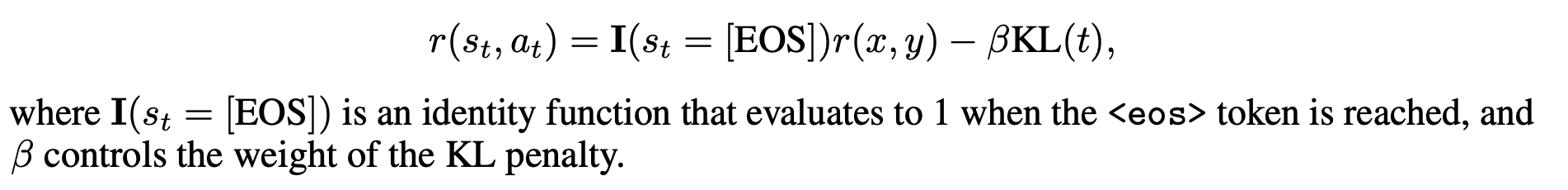
• GRPO 구현에서는 reward의 한 파트로 KL-divergence가 포함되진 않지만, loss에는 포함

  • 이 방법이 더 계산하기 간편하고, 불필요한 복잡성을 피한다고 함

• 그래서 본 논문에서도 GRPO와 같은 KL loss를 사용

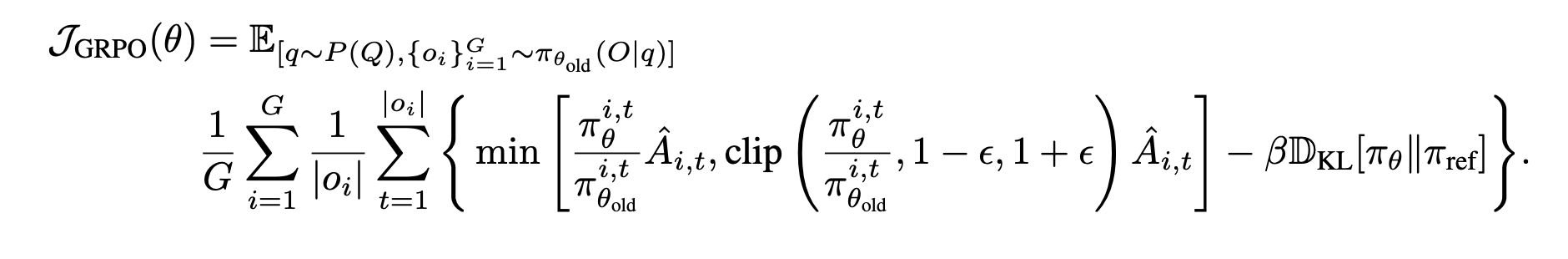
• Second ModificationL KL Estimation

  • PPO에서 사용되는 default KL estimator는 아래와 같음

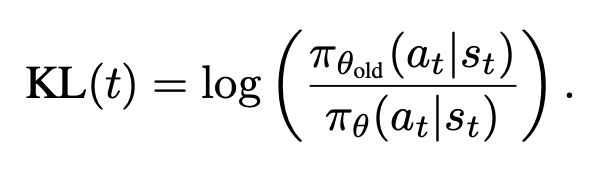
• 반대로 GRPO에서는 unbiased estimator를 사용

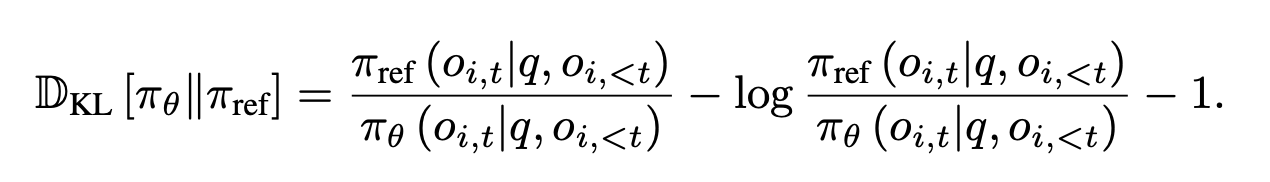
- 이렇게 할 경우 KL estimate이 항상 양수, 기본 버전은 음수값이 나올 수 있음

⇒ 학습할 때 GRPO가 더 안정적

Training Schedule

• 3600 step 학습, 4*10^-7의 learning rate, temperature 0.7로 사용

• 학습 동안에, logic puzzle의 등장 인물은 3-7명

Experiment

• Qwen 2.5 친구들을 주로 사용

  • Qwen2.5-Math-7B 모델의 경우 파이썬 코드 블럭을 생성하는 경향이 강함 ⇒ system prompt를 게저하고 markdown style에 패널티를 줘도 잘 안됨

    • Qwen2.5-Base와 Qwen2.5-7B-Instruct을 기본 모델로 테스트 해봤을 때, 거의 차이가 나지 않음

      • 학습 동안의 training metric이나, validation accuracy, response length growth curves, reward cruves 등

    • 하지만 instruct모델이 좀 더 높은 test acc를 보여서 기본 모델로 Qwen2.5-7B-Instruct-1M을 사용

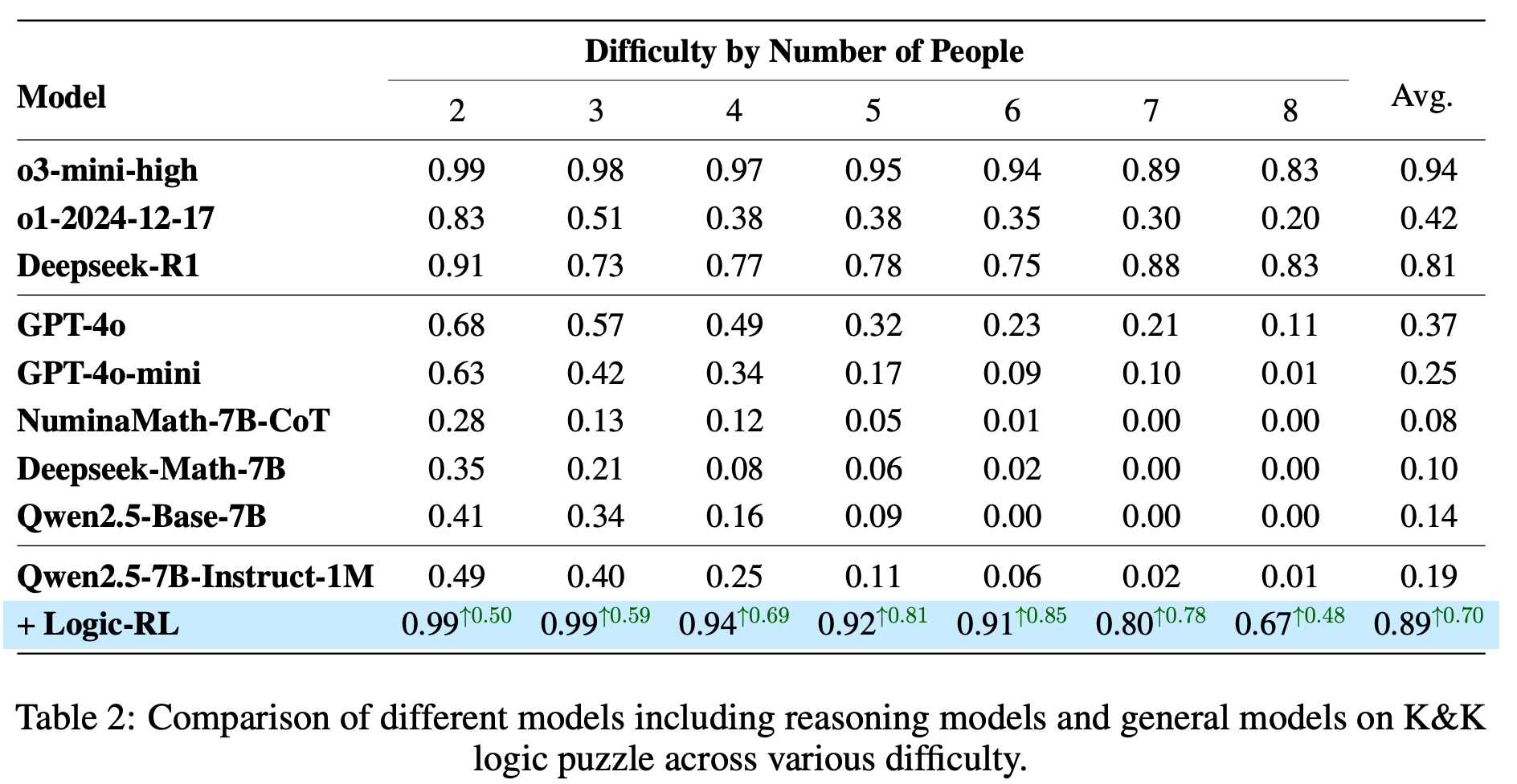
• 3-7명이 등장하는 K&K logic을 학습 데이터(<5k)로 사용, 8명이 등장하는 퍼즐을 OOD로 사용

• 처음엔 평균 500 token정도의 답변을 생성했지만, RL로 1K step정도 학습한 후에는 답변 길이가 거의 2K가 됨

  • 답변 길이가 길어지면서, 모델이 점점 복잡한 reasoning behavior(reflection, 다른 해결책 탐색 등)을 하기 시작

    • 이러한 현상은 학습 데이터와 관련 없이 자연스럽게 발생하고, 더 복잡한 태스크를 다루는 모델의 능력을 향상 시킴!

Research Question

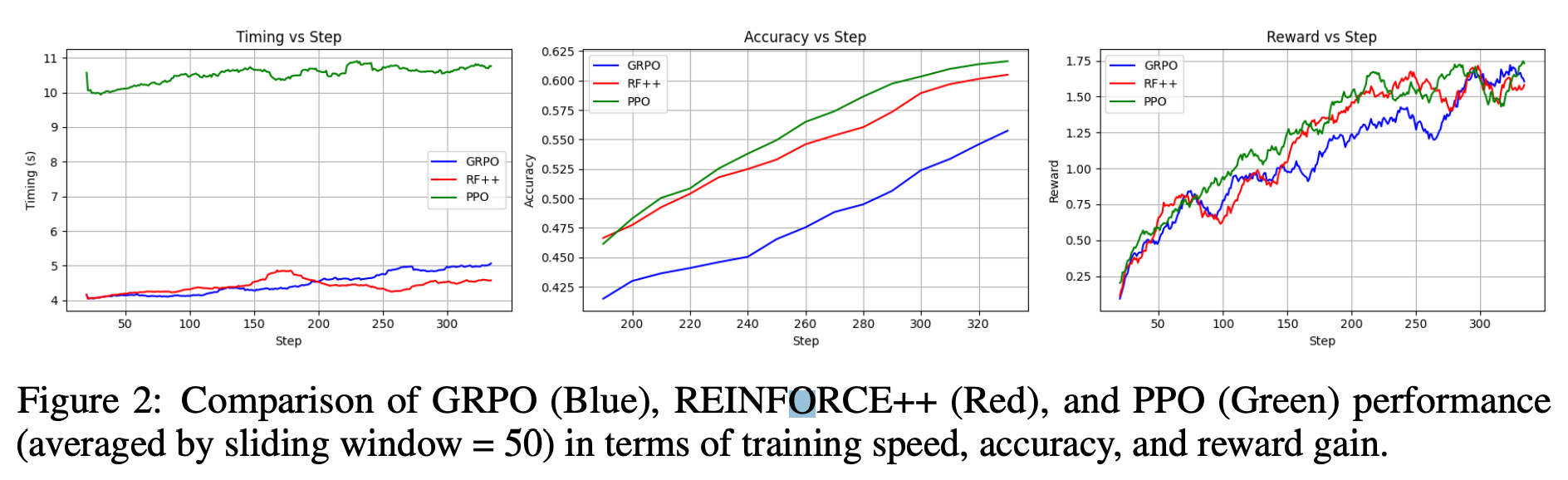
• RQ1 : How does GRPO Compare to Other RL Algorithms?

• PPO는 accuracy, reward에서는 높은 성능을 보이지만 너무 학습 속도가 느림

• REINFORCE++ 가 적당히 높은 성능, 빠른 학습 속도를 보임

• RQ2 : Do certain thinking tokens and language-mixing phenemona improve reasoning?

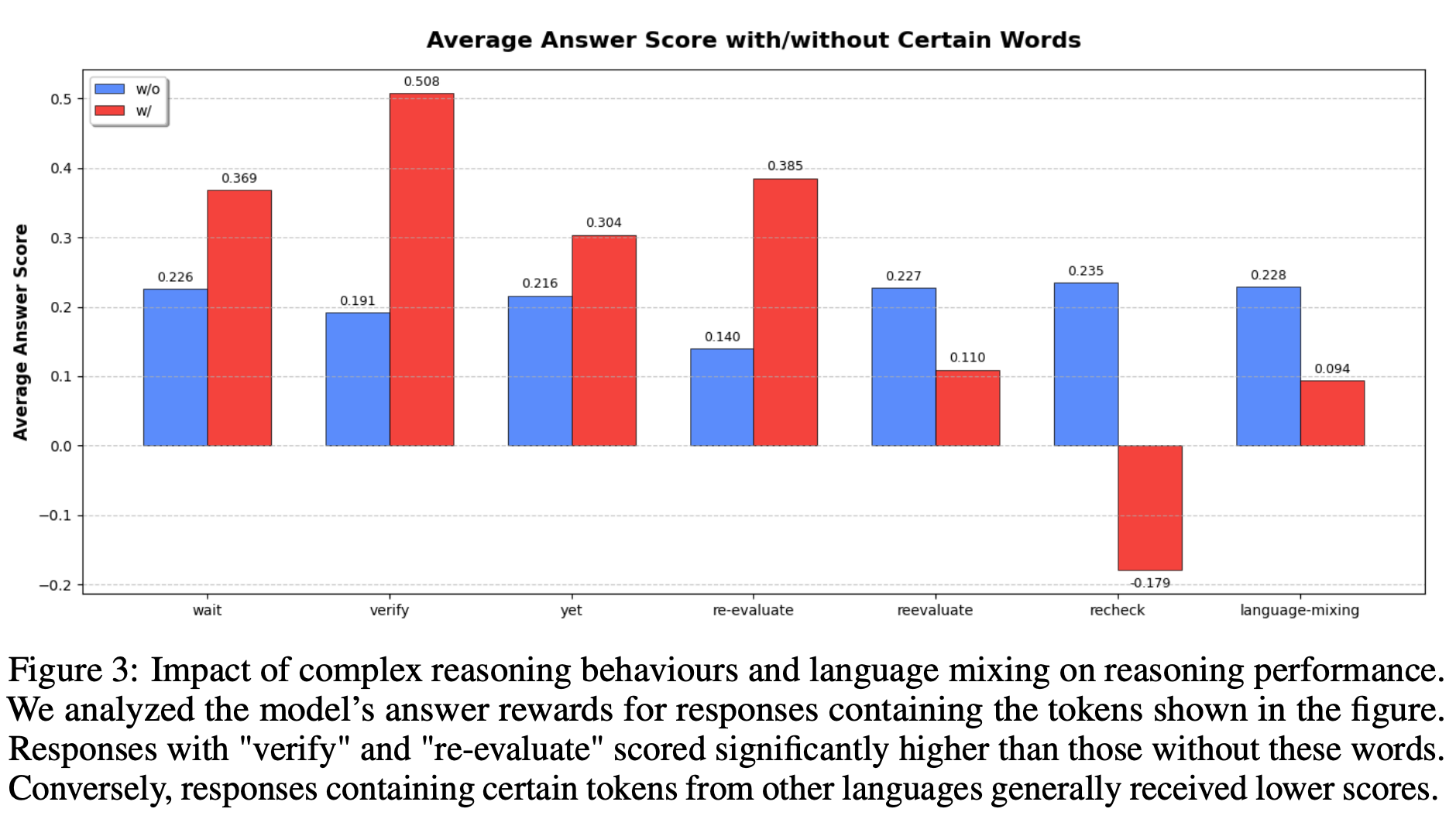
• 답변에 x축에 있는 단어들이 포함될 때의 answer score를 보여줌

• wait, verify, yet, re-evaluate 등의 단어가 포함되면 답변 성능이 좋아짐

  • 단 reevaluate이 등장하면 성능이 더 낮아지는데, 저자들이 확인해본 결과 “reevalaute”이 포함된 데이터가 별로 없다고 함

• reheck의 경우 성능이 낮아지는데, 이는 모델의 uncertatinty를 보여주는 signal이기 때문인 것으로 추정

• langauge-mixing reasoning 성능을 낮춤

• RQ3 : Does an ‘Aha Moment’ Emerge During Training?

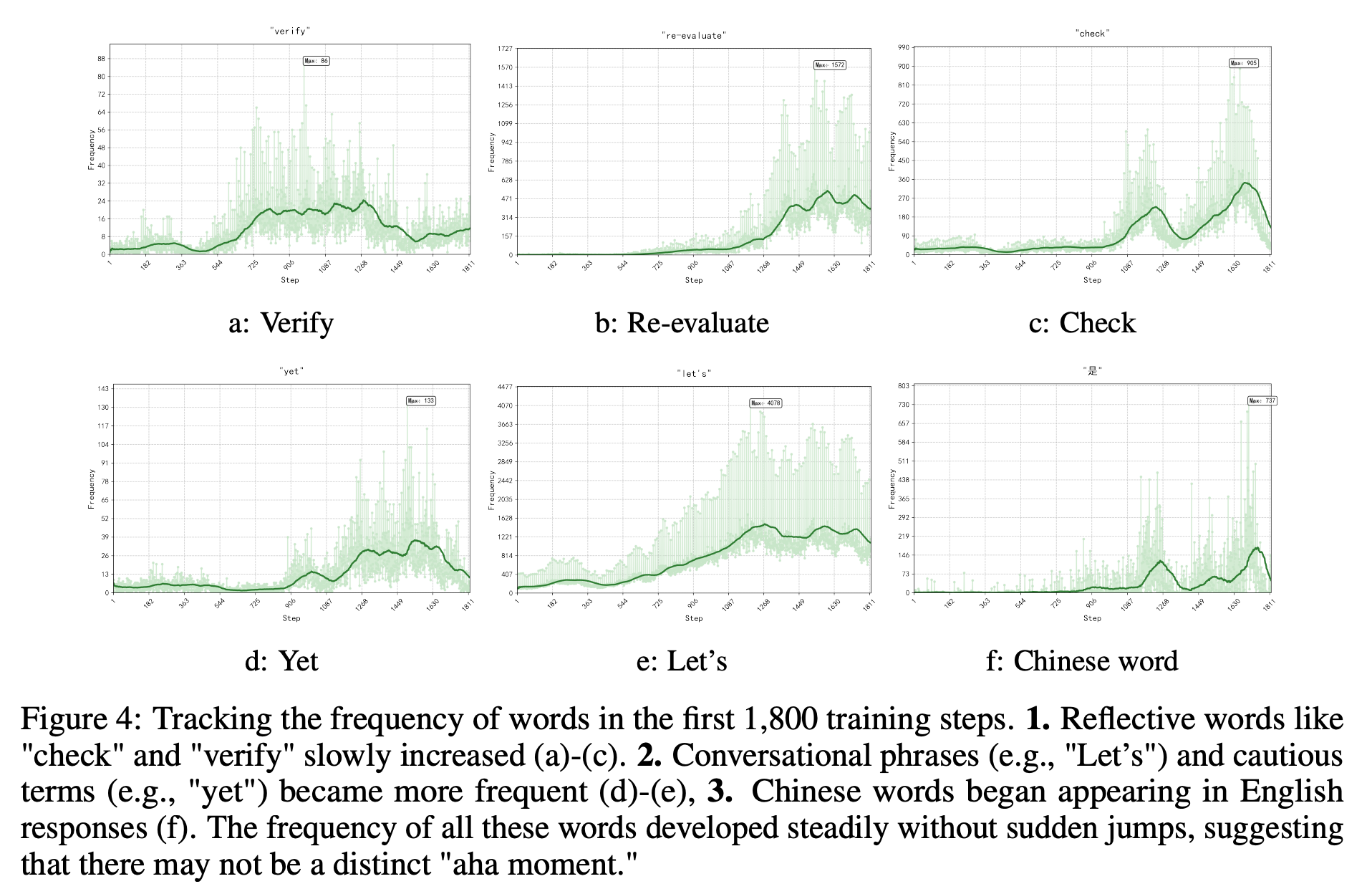
• 아하 모먼트는 모델이 갑자기 “Wait, wait. Wait. That’s an aha moment I can flag here.”와 같은 말을 생성할 때를 의미

• 하지만 위의 장표를 보면 complex reasoning behavior는 step 10에서도 종종 발생, 갑자기 확 빈도가 늘지 않음

⇒ RL process에서 갑자기 complex reasoning behavior가 발생하는거 같진 않음

• RQ4 : Can the Model Generalize to Out-of-Distribution (OOD) Tasks?

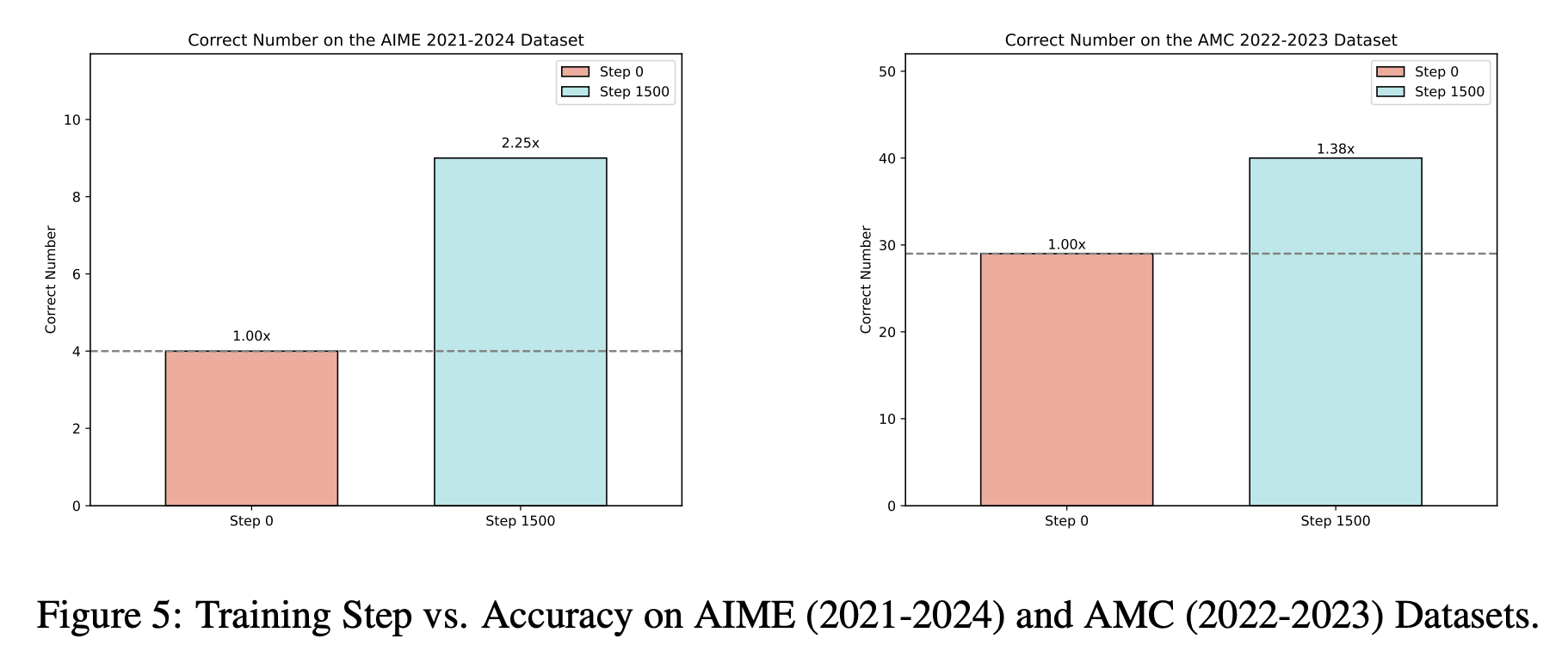
• K & K 로 학습하고, 수학 dataset으로 평가했을 때, base모델 보다 성능이 높음

⇒ RL이 in-distribution task에서의 모델 성능을 높이는 것 뿐만 아니라, robust, transferable한 reasoning strategies를 향상시킴

• RQ5 : Which Generalizes Better, SFT or RL?

  • 평가하기 위해 신기한 지표를 도입 (Local Inconsistency-based Memorization Score

    • ACC가 높은데 LiMeM의 점수가 높으면 in-domain에서만 잘한다는 뜻

    • ACC가 높은데 LiMeM의 점수가 낮으면 generalization이 잘된다는 뜻

• 일반화 성능을 평가하기 위해서 perturbation example을 사용

  • 한명의 statement를 다른 bool logic expression으로 바꾸거나, 각 사람의 말의 순서를 바꿈

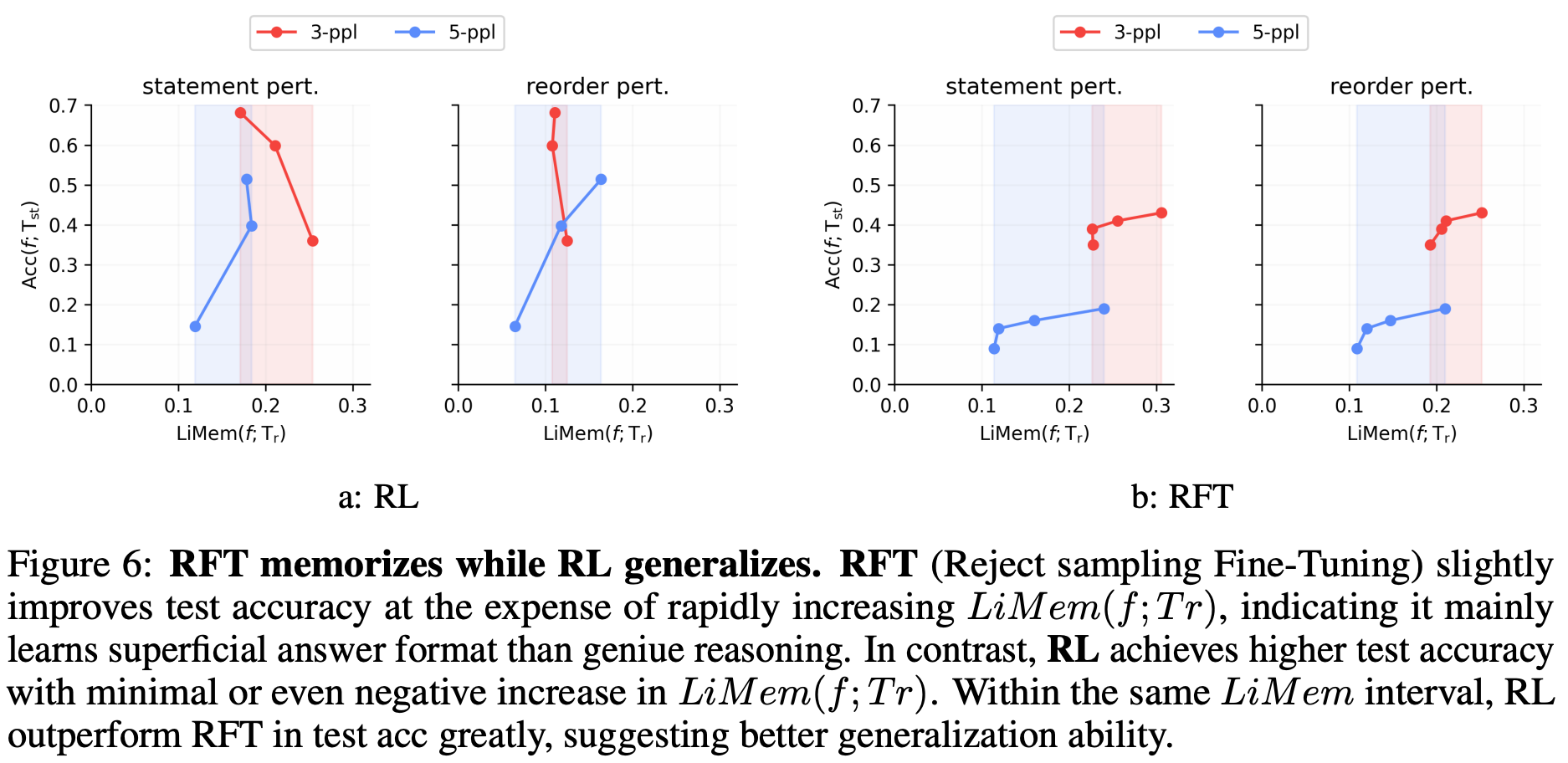
• 실험 결과, RFT(reject sampling fine-tuning)은 암기를 잘하고, RL은 일반화를 잘한다고 함…

  • 실험 장표 이해 불가

• SFT는 인위적인 alignment를 하고, RL은 좀 더 독립적으로 탐색, 일반화 능력을 기름

• RQ6 : Is Curriculum Learning Still Necessary in RL?

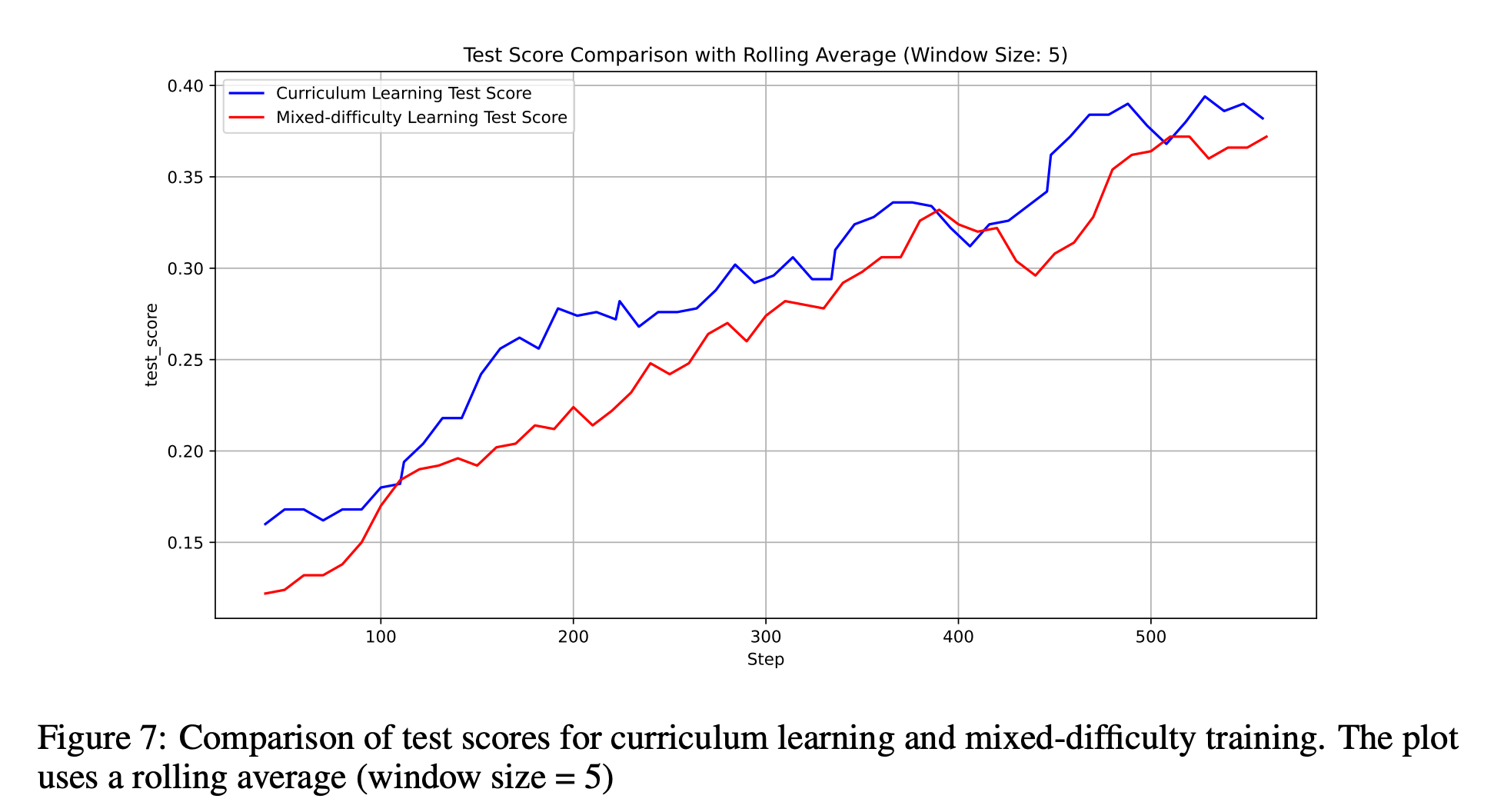
• 도움은 되지만 꼭 필요하진 않다!

• RQ7 : Does Longer Response Length Guarantee Better Reasoning?

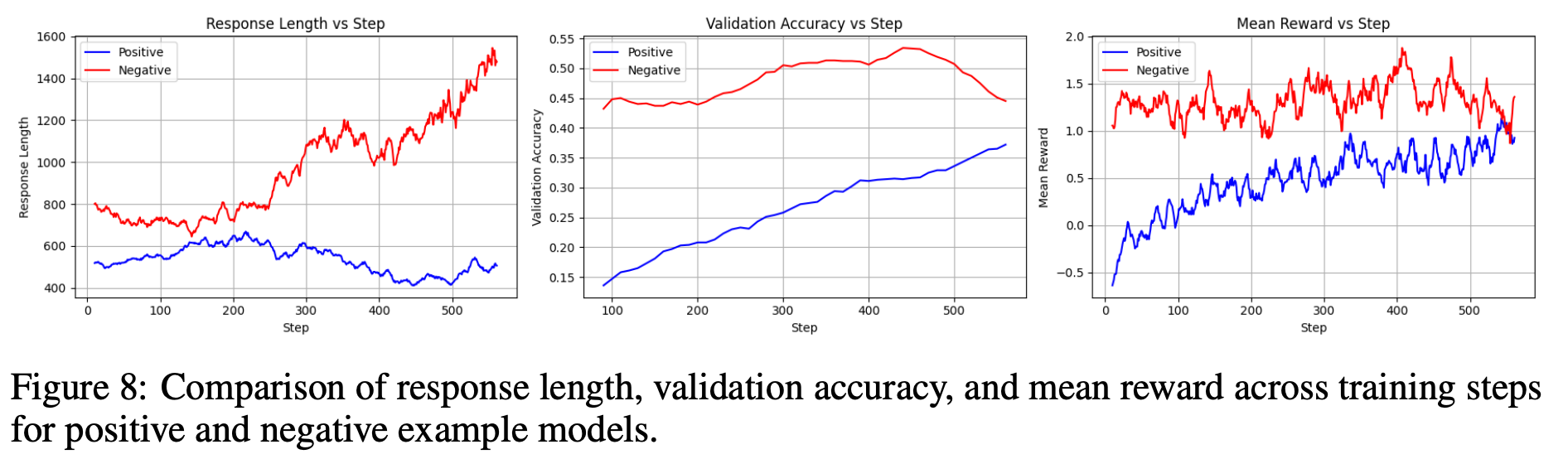
• 200 step 이후로 답변 길이가 증가, 하지만 성능은 비슷 ⇒ 긴 답변이 항상 더 나은 Reasoning을 보장하진 않음