ON THE EXPRESSIVENESS OF SOFTMAX ATTENTION: A RECURRENT NEURAL NETWORK PERSPECTIVE

Created on August 12, 2025

2025   ·   attention   efficient transformer   language-model   neural   paper-review   ·   paper-reviews

논문 정보

  • Date: 2025-08-12
  • Reviewer: Jaewon Cheon
  • Property: Efficient Transformer

선정 이유

  • 잘 쓴 논문은 아님; Rather Report 느낌

    • 오히려 논문으로서는 이런 논문들이 Contribution은 더 많음

  • Research Field 소개에는 나쁘지 않은 것 같아서..

0. Prerequisites

RQ: RNNs(Linear Attention)은 왜 Attention보다 LM 성능이 낮을까?

Prerequisites:

  • RNNs(Linear Attention) ?

  • Isn’t RQ seems so obvious ?

  • Is Attention - Softmax = RNNs(Linear Attention) ?

  • RNNs(Linear Attention)

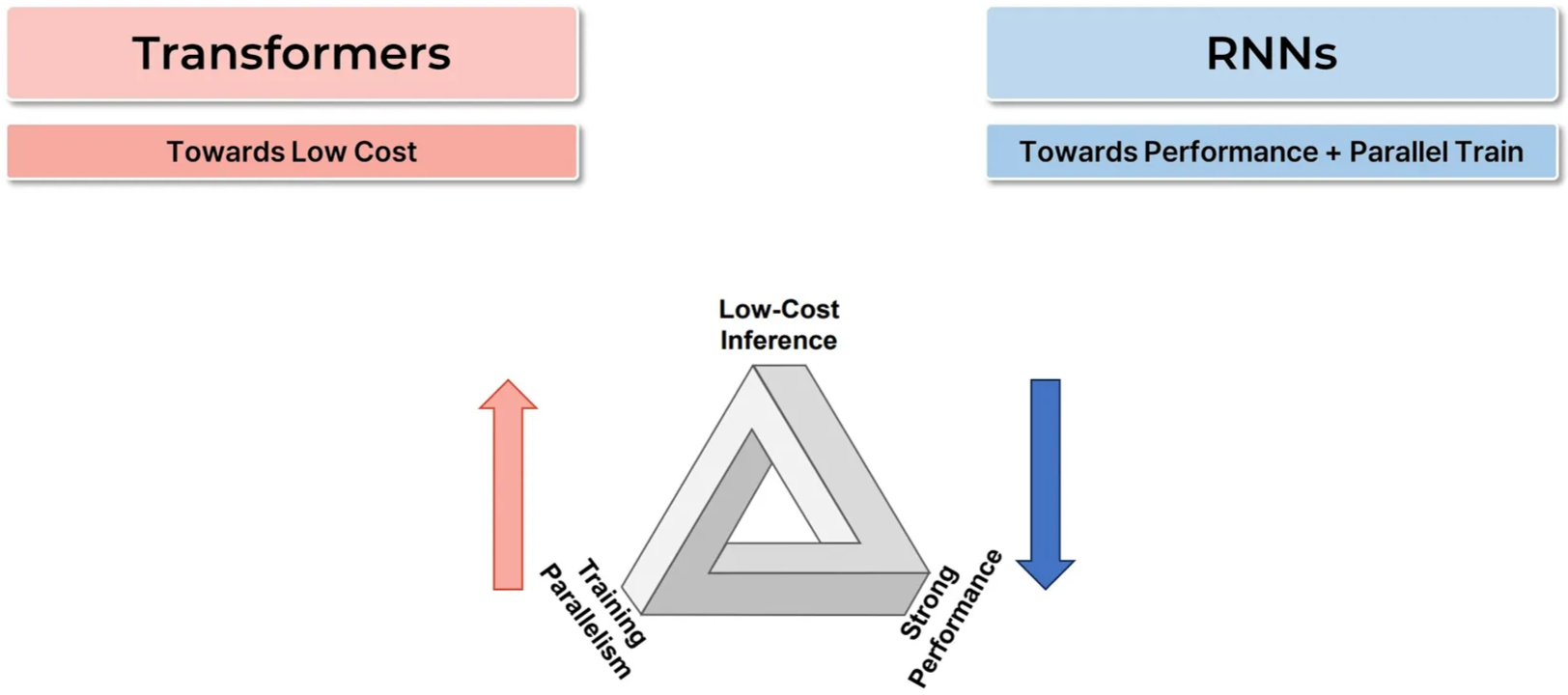
  • Inference Cost는 TF-based Language Models의 가장 큰 내재적 한계들 중 하나

    • KV Cache Complexity = O(N)

    • Attention Complexity(per query) = O(N)

  • RNNs(Mamba, RWKV, Titans, …)는 Sequential Information을 고정된 State에 저장 → 가장 직관적인 한계 극복 방법

    • KV Cache Complexity = O(1)

    • Attention Complexity(per query) = O(1)

  • But, Training Parallelism 및 Weak Performance가 해결해야 할 과제

    • Training Parallelism → 꽤 많이 해결되었음

    • Performance → 근본적으로 해결이 안 될 것처럼 보임

  • Is Attn vs RNNs a obvious fight?

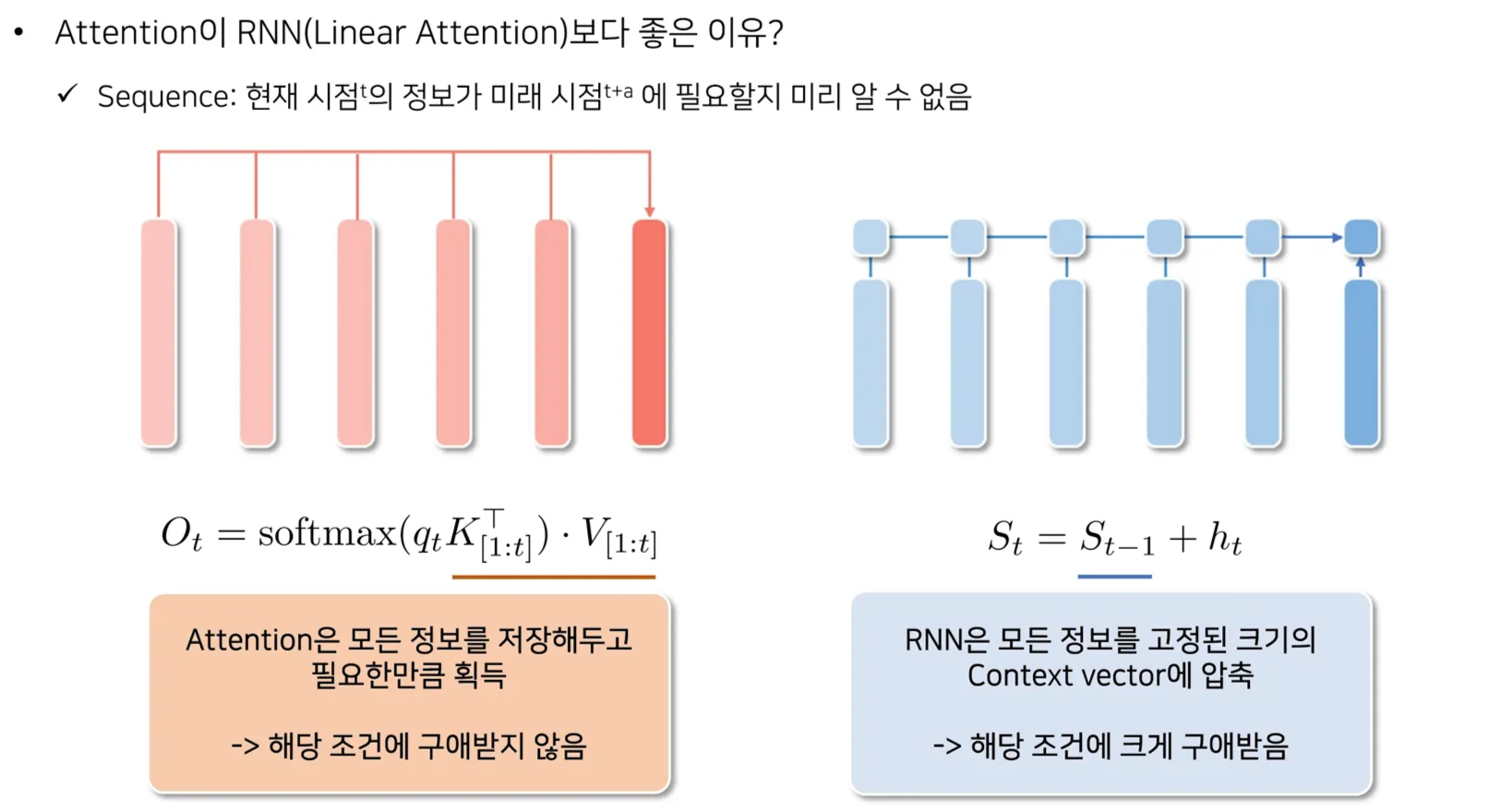
  • 위와 같은 Intuition이 있음

    • Attention: q에 따라 필요한 정보를 모든 KV들에 대해 선택적으로 가져옴

    • RNNs: q가 무엇이든 고정된 S에서만 정보를 가져올 수 있음

  • Attention w/o Softmax is RNN!

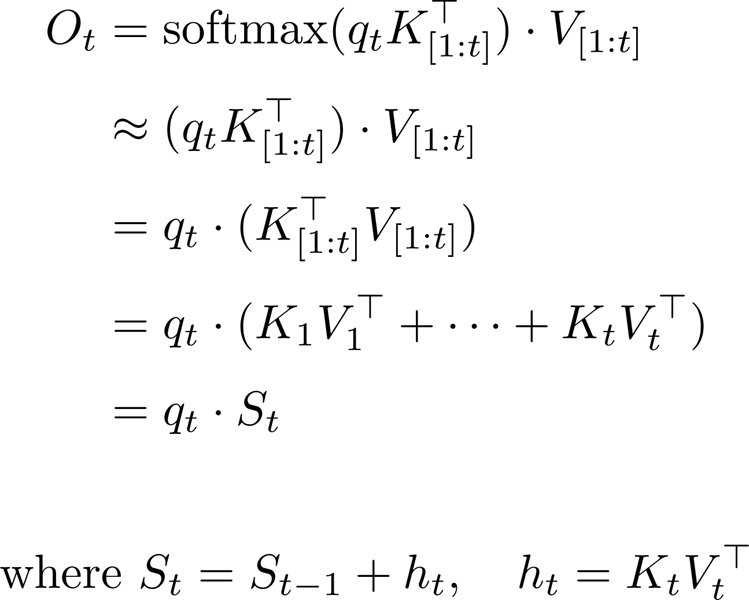
  • Line 1: Attend Property는 (qtK^T{1:t})를 하기 때문에 발생

  • Line 2 : Softmax 연산을 빼더라도, 여전히 qt가 모든 K{1:t}, V_{1:t}에 Attend하는 것은 동일

  • Line 3 : Associativity

  • Line 5 : 이는 고정된 State S_t에서 정보를 가져오는 것과 같음

  • Line 4: Moreover, 이 S_t는 각 시점 1…t에서 만들어지는 KV의 Outer Product로 Update됨

    • 굉장히 간단한 RNN Update Rule

  • 즉, Softmax(유일한 Non-linearity)가 없는 Attention은 RNN → Linear Attention이라 명명

  • 제 Attend Property는 어디갔나요?

    • Attention
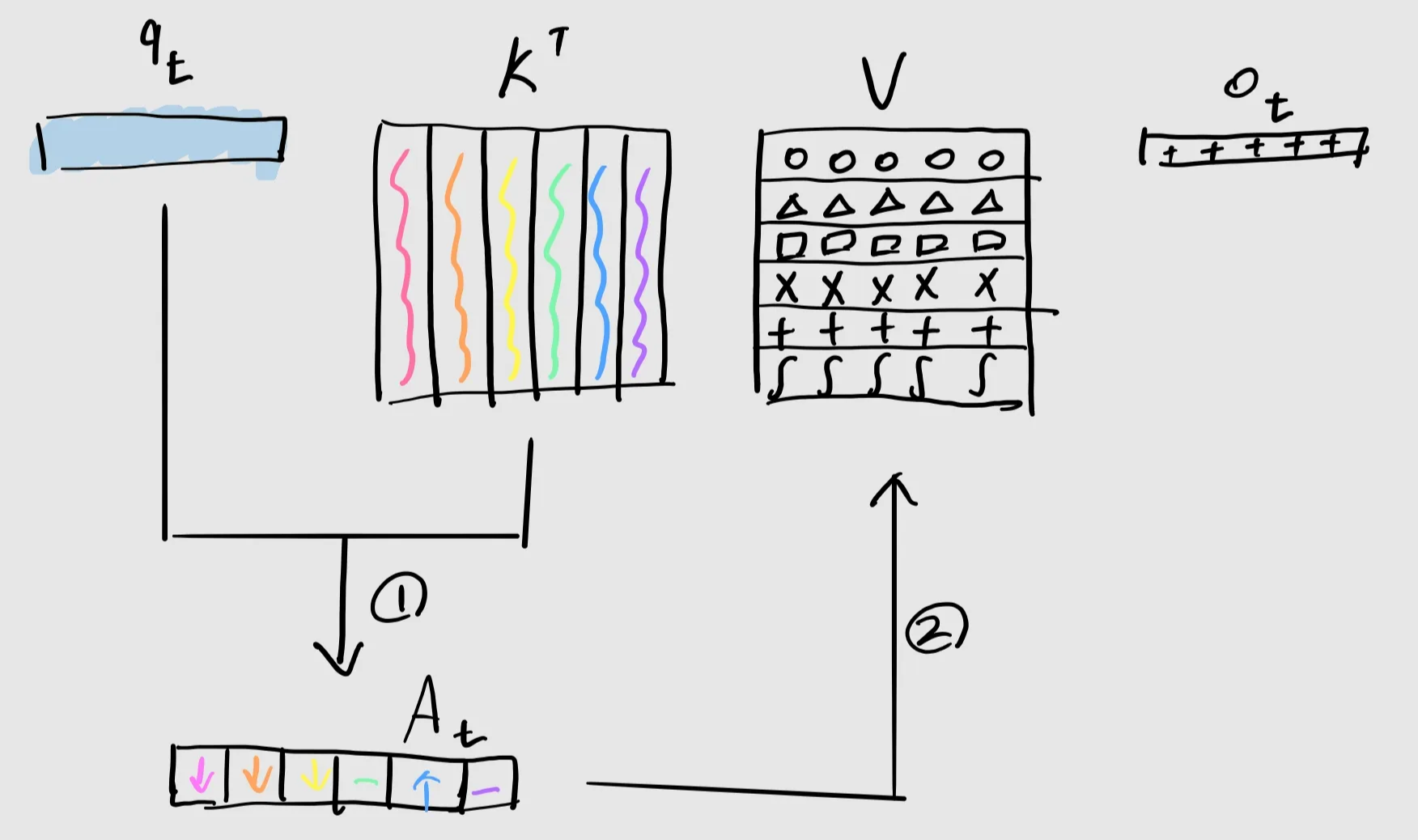
- Linear Attention

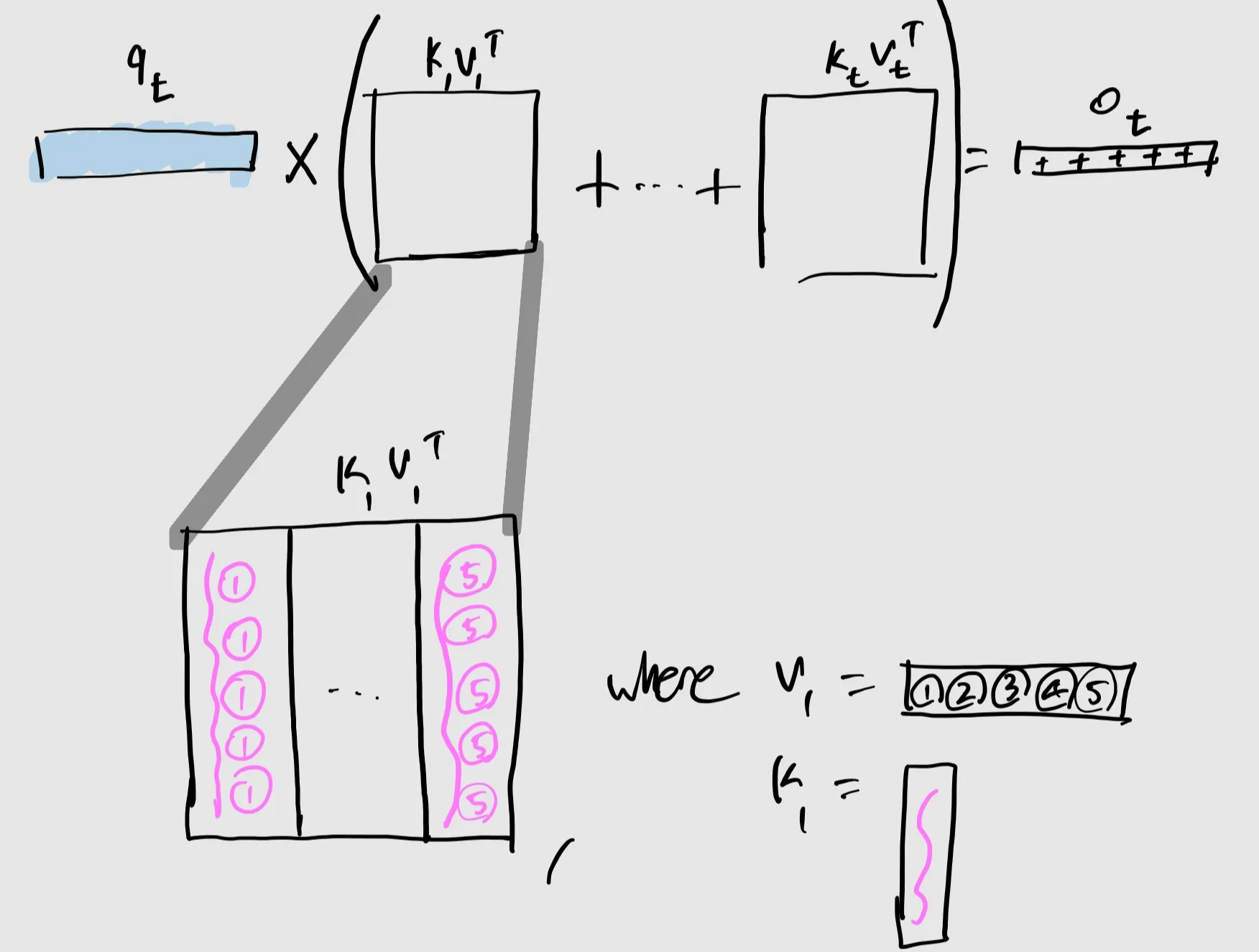
  • Attention과 RNN의 차이는 위와 같은 Intuition에서 오는 것이 아닌, Softmax에서 오는 것

    • Challengeable

1. Intro

RQ: RNNs(Linear Attention)은 왜 Attention보다 LM 성능이 낮을까?

Prerequisites:

  • RNNs(Linear Attention) ?

  • Isn’t RQ seems so obvious?

  • Is Attention - Softmax = RNNs(Linear Attention)?

2. Recurrent-style Softmax

  • Objective : Softmax를 RNNs로 reformulate ⇒ 기존 RNNs의 요소들과 비교, Weakness 파악

  • Softmax를 Approximate하지 않고, Linearize할 수는 없을까?

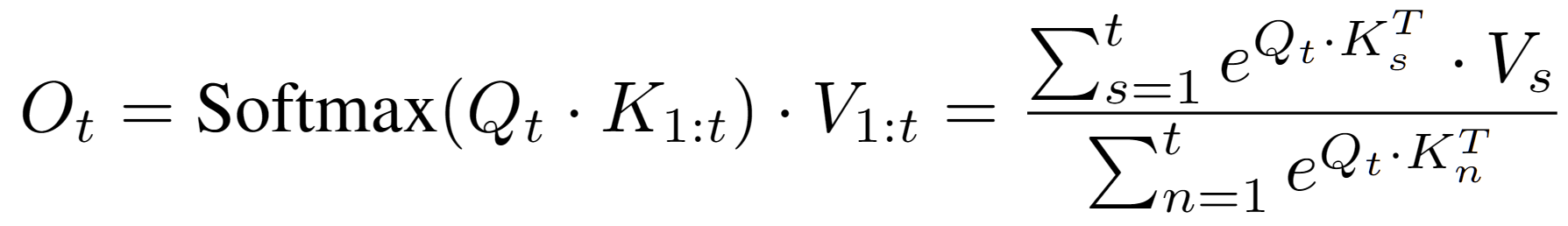
  • e^{Q\cdot K^T}연산을 분리해야 함 → 보통 아래와 같이 Kernel Trick을 써서 표현

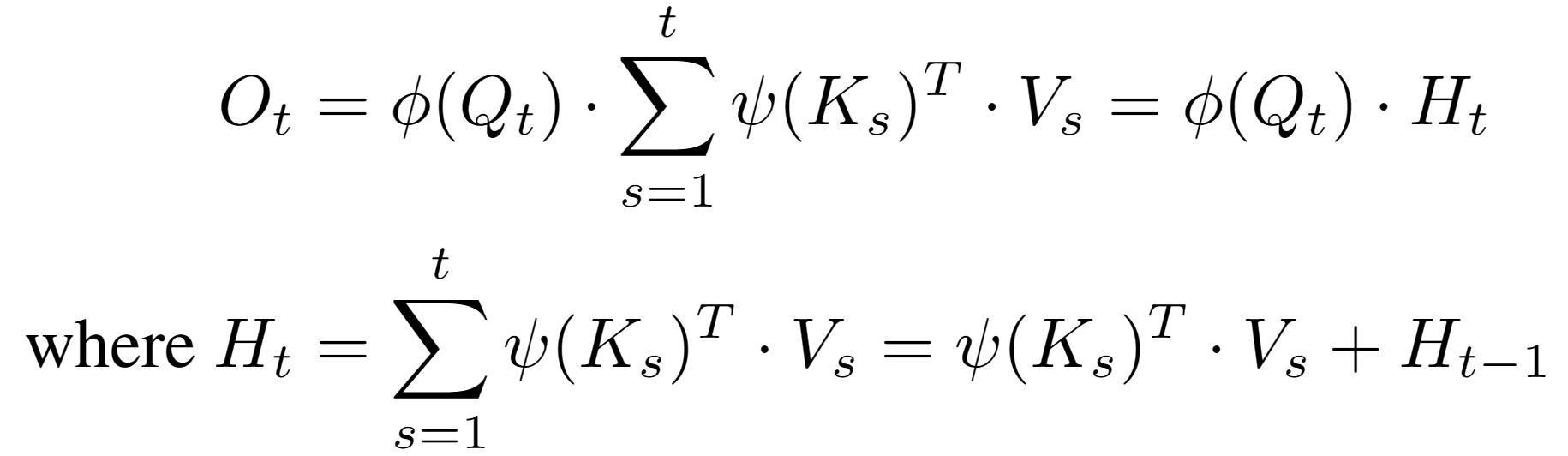
  • 이 때, Exponential에 Taylor series expansion을 사용하면 Approximate 없는 Linearize 가능

    • Softmax를 RNN화했을 때, 어떤 일이 일어나는가?
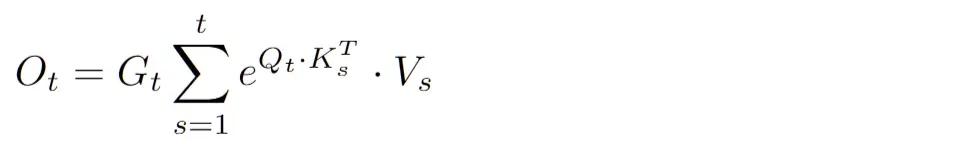
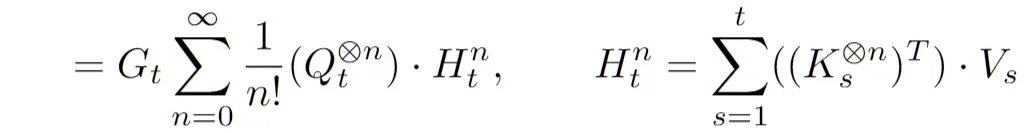
- **증명**

  - Taylor Expansion

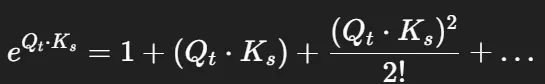
  - Prove
  • \otimes: n차 tensor product

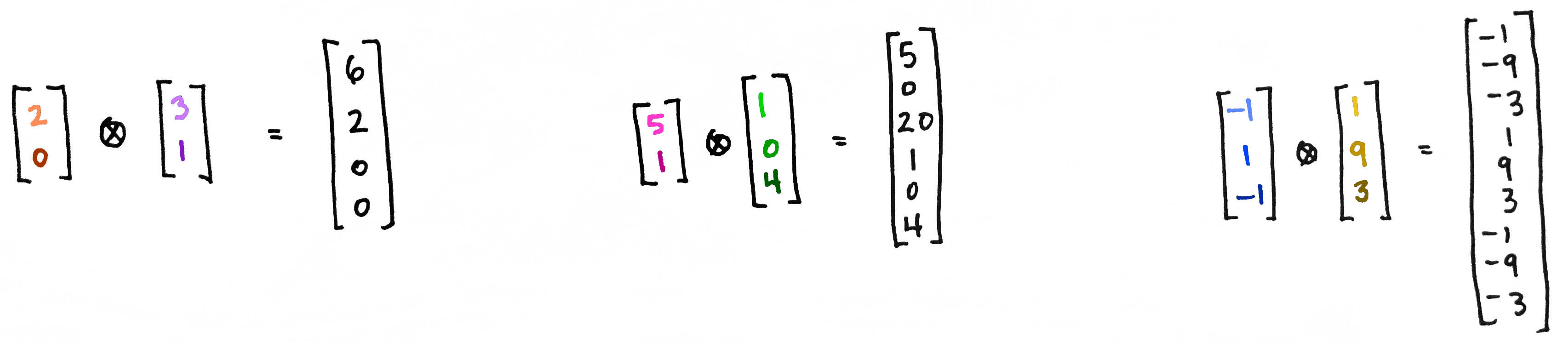
  • 결국 Recurrent Softmax는…

    • e^{Q⋅K}의 테일러 전개로부터 도출되는 1차항부터 무한차항까지의 RNN을 전부 더한 연산

    • 각 RNN 출력에는 계수 \frac{1}{n!}가 곱해짐

    • 각 RNN의 hidden state 차원

      • n차 항의 hidden state 크기: \mathbb{R}^{d^n\times e}

      • d = K(Q) 차원, e = V 차원

  • 이는 아래와 같은 두 Term으로 나뉨

    • Q, K 벡터의 Infini-Sum with 높은 차수에 대해서는 매우 낮은 가중치를 곁들인… → 분자

    • 위 연산들의 합에 대한 Inverse G_t → 분모

4. Numerator

  • 분자의 Infini-Sum 중, n=1만 사용하면?

    • Linear Attention과 동일!

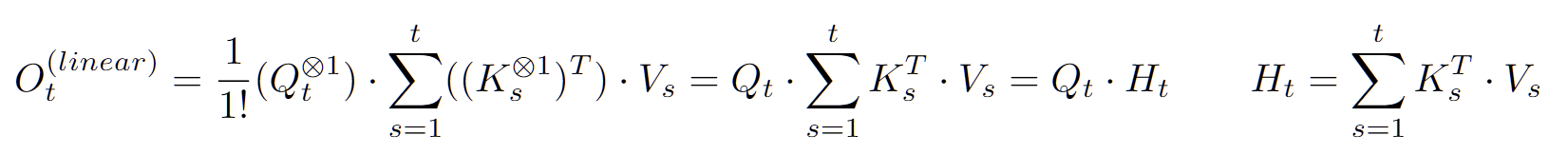
  • 결국 (Primitive) Linear Attention은 Softmax Attention의 First-order approximation이었던 셈

  • 무한 개의 State를 사용하는 것과 같은 Softmax Attention에 비해 하나의 State만 사용하고 있는 것으로 해석

  • Or, Softmax Attention의 고차항 Interaction을 무시하는 Approximation으로도 해석할 수 있음

  • 그럼, 고차항의 Interaction과 그에 대한 State를 추가하면, RNN의 성능이 좋아지는가?

    • ⇒ YES!

5. Denominator

  • G_t는 Recurrent Architecture에서 동치되는 무언가를 찾기 애매

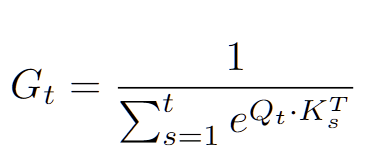
  • Original G_t는 Attention score의 Exact Normalization를 수행

    • Score의 확률분포화 ⇒ 크게 중요하지 않을 수도…? (i.e. Quite Attention, …)

    • Output에 대해 곱해지는 어떤 값이라고 일반화를 하여 취급 ⇒ 비슷한 역할을 하는 요소가 존재

  • G_t as a Gate

    • 보통 RNNs에는 Output의 크기를 조절하는 Learnable Gate가 존재

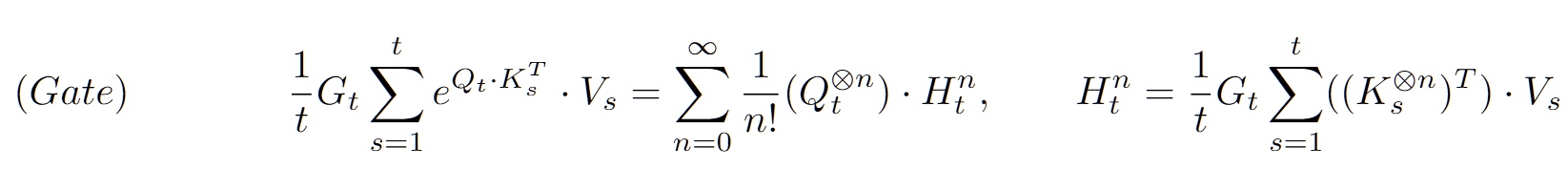
  • 하지만 결정적으로, Sequence length가 길어짐에 따라(많은 Vs가 추가됨에 따라) exploding을 막을 수 없다는 점에서 기존의 G_t와 다름

  • G_t as a Norm

    • Adaptive Gating이 중요하다기보다는, exploding을 막을 수 있게 Normalize를 하는 것이 중요할 수 있음

      • C.f. Normalize score vs Normalize output

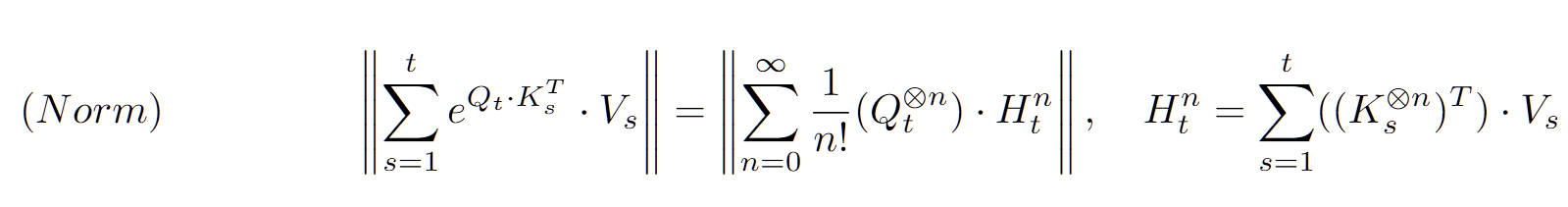
  • 그럼, G_t를 Attention Score의 Summation이 아니라, 거리 기반의 Normalization Term으로 바꿔도 Softmax의 성능이 유지되는가?

    • ⇒ YES!

6. Results

  • 실험 세팅

    • Model: Llama-2 사용

      • 사실 Setting만 사용

      • 300M ~ 2B

    • Dataset:

      • Pile

      • Slimpajama

      • Fineweb

    • Training

      • NTP from scratch

    • 그 외

G_t as a Norm

  • Numerator: exponential로 고정

  • Denominator: Softmax(기존) / Norm(L2) / Gate(Learnt)

  • Model size: 300M(…)

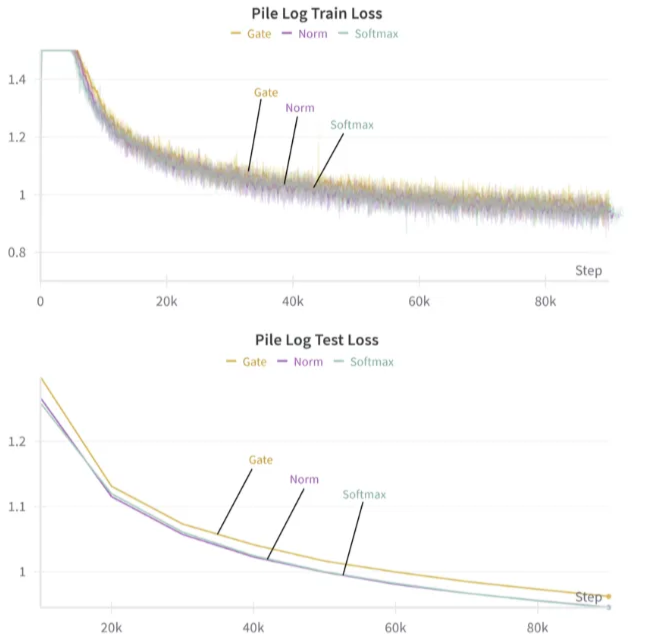
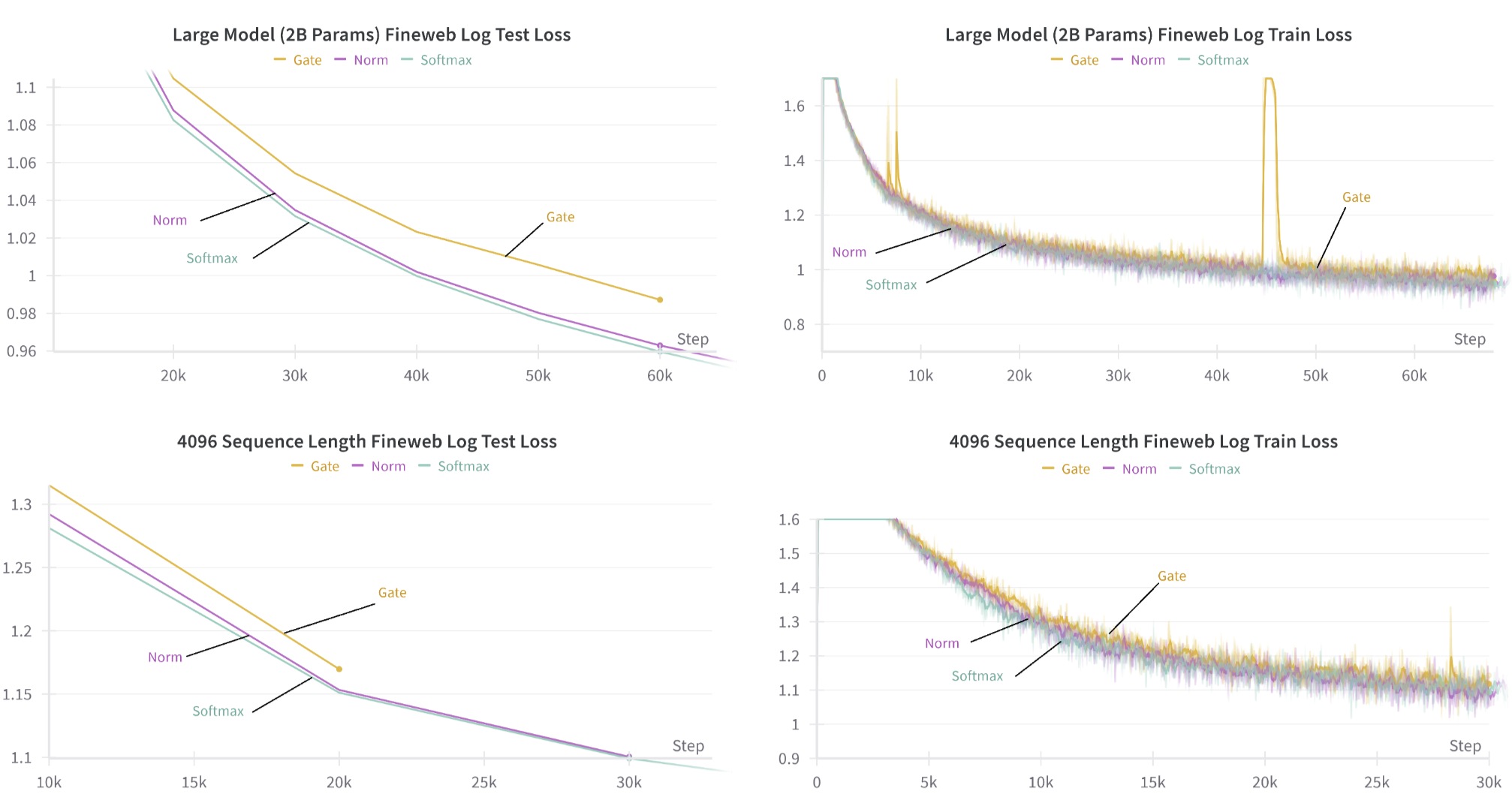
  • Gate의 경우 학습이 Unstable하고, 성능도 Softmax에 비해 많은 차이가 남

  • Norm은 학습도 Stable, 성능도 Softmax와 비슷

    • Softmax Denominator == Norm operator라고는 할 수 없겠지만, 적어도 오늘날 많이 사용되는 Gate로는 부족하다는 말을 할 수 있음

  • Scaling을 했을 때, 이러한 경향은 더 심해짐

Taylor series Expansion

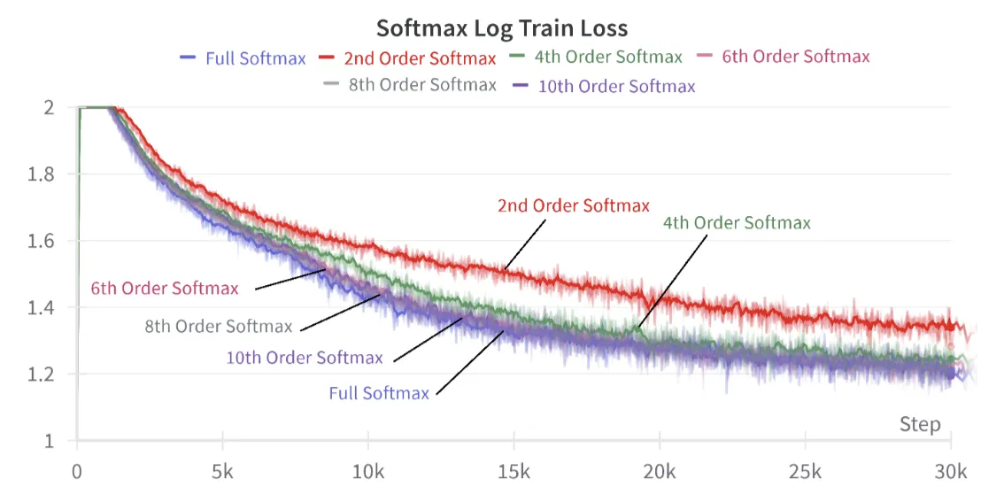
  • Order가 추가될수록 Full Softmax의 원래 성능을 회복하는 것을 확인

    • 10th Order 정도면 완벽히 성능 복원이 되는 것을 확인할 수 있음

  • 물론, 그렇다고 해서 10th Order Update을 구현하는 것은 Infeasible하겠지만…

    • 적어도 Full Softmax(O(N))에 Comparable한 Recursive formula(O(1))를 볼 수 있는 것은 신기한 부분

7. Conclusion

  • Softmax는 무한차수의 RNN Summation + Norm Denominator이다! (Roughly)

  • Limitation

    • Up to date RNNs들에 적용했을 때의 결과가 없음

    • Model size와 Downstream task에서 제한되어있는…