ON THE GENERALIZATION OF SFT: A REINFORCEMENT LEARNING PERSPECTIVE WITH REWARD RECTIFICATION
논문 정보
- Date: 2025-08-19
- Reviewer: 전민진
- Property: RL, SFT
standard SFT gradient는 내재적으로 모델의 일반화 능력을 제한하는 reward를 갖고 있음. 이를 RL과 유사하게 loss 수식을 변경해 더 높은 성능을 내보자!
Abstact
-
간단하지만 이론적으로 영감을 받은 향상된 SFT방식을 제안
- RL과 비교하여, 제한된 generalization 문제를 다룸
-
수학적인 분석을 통해서, 기본 SFT gradient가 내재적으로 모델의 일반화 능력을 제한하는 reward를 갖고 있음을 밝힘
-
이를 수정하여, Dynamic Fine-Tuning(DFT)를 제안
-
각 토큰에 대한 gradient updates를, 각 토큰의 확률로 objective function을 dynamic하게 rescaling해서 안정화
-
특히, 코드 한 줄만 바꿔서 SFT보다 여러 데이터셋에서 훨씬 높은 성능을 보임
-
또한, DFT는 offline RL설정과 비슷한 결과를 보이며, 효과적이면서 더 간단한 대안을 냄
-
Introduction
-
expert demonstration dataset에 모델을 학습시키는 방법론인 SFT는 LLM을 새로운 태스크나 도메인에 adapt할 때 사용하는 기본적인 post-training방법론
-
가장 구현하기 쉽고, 전문가스러운 행동을 가장 빠르게 습득
-
하지만, RL에 비해서 generalization 성능이 제한적이라는 한계가 존재
-
-
RL은 명시적인 reward나 verification signal을 사용, 모델이 좀 더 다양한 strategy를 탐색할 수 있게 해 더 높은 일반화 성능을 달성
-
하지만, computational cost가 상당함 + hyperparameter tuning에 민감 + reward signal을 쓸 수 있을 때만 활용 가능 ⇒ 이 모든 조건이 다 맞기는 쉽지 않음
-
RL이 가능한 경우에도, SFT는 RL이 스스로 학습하기 어려운 정답 패턴을 빠르게 학습하는데는 여전히 유리
-
-
이러한 상보적인 특성 덕분에, 최근 연구들은 보통 SFT와 RL을 함께 사용해서 모델을 학습함
⇒ 하지만 SFT만으로 RL에서 얻는 효과를 어느정도 얻을 수 있다면? 아주 나이스함
-
SFT는 negative sample 혹은 reward, vefication model이 없는 경우에도 활용할 수 있음
-
본 논문에서는, SFT와 RL사이의 근본적인 차이를 밝히는 수학적 분석을 통해서 제공하여 이러한 차이를 해소하려고 함
-
SFT의 gradient update가 (내재적으로 정의된 reward structure를 갖는) policy gradient method의 한 케이스로 해석될 수 있음을 보임
-
저자들의 분석에 따르면, 이러한 implict reward가 극단적으로 희소하면서 expert action의 배정된 policy에 반비례함을 보임 ⇒ 그래디언트는 무한한 분산을 겪게 되어 안좋은 최적화 환경을 만듦
- 정답 데이터의 확률이 땅바닥에 있으면 reward가 매우 커지는.. 그런 문제가 있음
-
-
이러한 수학적 분석에 기반, Dynamic Fine-tuning(DFT)를 제안
-
ill-posed reward structure의 근원을 해소
-
간단하게, 각 토큰의 확률로 SFT objective를 rescaling ⇒ 예기치 못한 reward structure와 무한한 분산을 야기하는 inverse probability weighting를 효과적으로 중화 ⇒ 확률 의존적인 gradient estimator를 안정적이고 균일하게 가중된 업데이트로 변환
-
-
실험 결과, Qwen2.5-Math Modeles를 NuminaMath dataset에 학습하여 SFT보다 높은 성능을 보임.
- 특히, SFT는 AIME 2025, Olympiad Bench 등을 포함한 어려운 데이터셋에 대해서 performance degradation 현상을 보이는 반면, DFT는 상당한 성능 향상을 보임
-
또한, RL senarios안에서 비교
- RFT/RAFT, DPO보다 높은 성능을 보일 뿐만 아니라, GRPO, PPO와 같은 online RL과도 뒤지지 않는 성능을 보임
-
DFT가 모델에 어떻게 다르게 영향을 미치는지 분석하기 위해, 학습 후의 확률 분포의 변화를 분석
- standard SFT의 경우 학습 데이터에 더 가깝게 맞추기 위해 토큰 확률을 일률적으로 높이는 반면에, DFT는 학습 세트에서 멀어지게도 만듦
Related Work
-
SFT과 RL의 trade-off는 language model alignment에서 핵심 주제
-
SFT는 expert demonstration을 따라하는데 있어 간단하고 효율적이여서 널리 사용됨
- overfitting와 RL보다 geneeralization이 좋지 않다는 한계가 존재
-
최근에 SFT는 외우지만 RL은 일반화한다는 분석도 존재
-
RL 학습이 효과적이기 위해선 초반에 output format을 안정화해야하는데, 이 때 SFT가 필수적
-
RL을 실제로 사용하려고 할 때, 쓰기 어려운 조건일 경우가 많음
- reward를 명시하기 어렵다던가.. computational cost가 제한적이라던가.. 등
-
-
-
최근엔 그 둘의 장점을 모두 활용하기 위해서 hybrid method에 집중을 하고 있음
-
SFT 후 RL-based refinement : 학습된 reward model(like InstructGPT)을 활용
-
SFT와 RL의 학습 단계를 번갈아가면서 시행 : 안정성을 높이면서 성능도 높이기 위해
-
DPO : reward model없이 postive answer, negative answer를 활용하여 imitation과 reinforcement signal을 하나의 loss에 녹여냄
-
Negative-aware Fine-Tuning(NFT) : 모델이 틀린 부분을 학습하여 스스로 개선할 수 있도록 함
-
⇒ 다 좋은 방법들이지만 reward signal, preference pairs or negative samples이 있어야 함
⇒ traning pipeline을 합치는 방법론이지 positive expert demonstration만을 사용하는 SFT 자체를 향상시키는 방법론은 아님
-
SFT와 RL을 이론적으로 통합하려는 연구 라인도 존재
-
RLHF를 SFT의 reward-weighted로 reframe, 파이프라인을 단순화, explict reward에 의존하는건 동일
-
SFT는 implicit reward를 가진 RL로 볼 수 있다는 것을 증명, vanishing KL constraint를 관리하기 위해 더 작은 lr를 사용하는 방법론을 제안
-
positive, negative feedback에서 학습하는 것을 분석, 이 둘의 balance가 policy covergence에 어떻게 영향을 끼치는 지를 보임
-
SFT를 RL의 lower bound로 reframe, data-generating policy에 기반해서 importance weighting을 도입해 향상 시킴
-
⇒ 이러한 경구들은 SFT와 RL 사이의 연결고리를 weigthing의 관점에서 지적, SFT gradient과 off-line policy gradient 간의 간단한 수학적 equivalence를 보이는 것에는 한계를 보임
-
반대로 본 논문에서는 equivalence를 엄격하게 확립한 최초의 연구, 핵심적인 차이가 SFT에 존재하는 inverse-probability weighting term에 있음을 보임
-
흥미롭게도, 본 저자의 방법은 잘 알려진 Focal Loss와 정반대되는 CE loss 설계를 도출
-
our modified CE : -plog(p)
-
focal loss : -(1-p)^\gamma log(p)
-
focal loss의 경우 소수 클래스에 대한 성능을 개선하기 위해, 잘 분류된 샘플의 가중치를 의도적으로 낮추지만, 본 논문에선 일반화를 개선하기 위해 잘못 분류된 샘플의 가중치를 의도적으로 낮추는 방식
- 요즘엔 underfitting이 overfitting보다 더 문제니까.. 라고 함.
-
Method
Preliminaries
- Supervised Fine-Tuning

- Reinforcement Learning

-
\nabla \theta를 Expectation 안에 넣는 과정
- 여기서 적분 형태로 식을 재작성
(편의상 x에 대한 기대값은 잠시 생략)
- 여기서 로그 미분 트릭 \nabla log(f(z))=\nabla f(z)/f(z), \nabla log(f(z))f(z)=\nabla f(z)을 사용하면, 아래와 같이 변형 가능
⇒ 아까 생략했던 x에 대한 기대값을 추가하면 4번식과 동일!
Unify SFT-RL Gradient Expression
-
2번의 SFT gradient식은 fixed demonstration distribution
-
이를 importance weight를 추가하여 on-policy expectation으로 변환해보자!
- expert (Dirac Delta) distribution과 모델 분포를 비교하는 importance weight를 도입
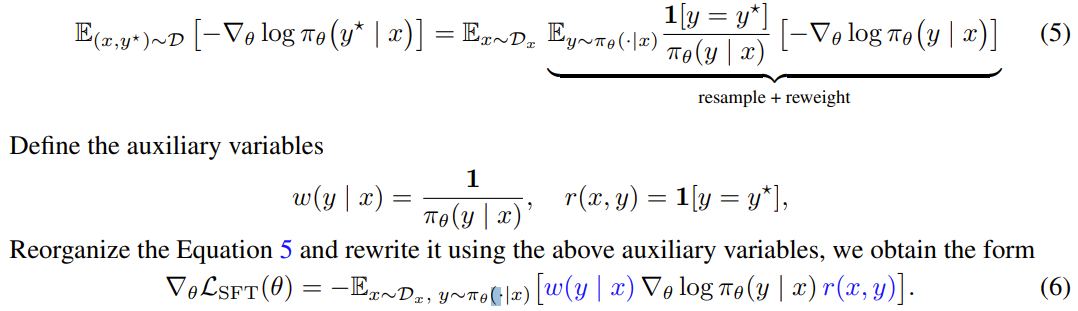
-
SFT gradient의 형태는 policy gradient equation(4번식)과 거의 유사
-
즉, 여기서 conventinal SFT는 reward를 expert trajectory와 동일한지를 비교하는 indicator function으로 주면서, importance weigthing 1/\pi_\theta로 편향된 on-policy-gradient로 해석 가능
⇒ 만약 모델이 정답을 맞힐 확률이 매우 낮으면, 가중치가 폭증, 학습 과정을 불안정하게 만들고, 모델이 어쩌다 맞춘 exact-match demonstration에 과적합되도록 함.
⇒ 학습 데이터의 특정 사례만 암기, 새로운 데이터에 대한 일반화 능력이 저하됨
Proposed Method
-
이러한 skewed reward issue를 좀 완화하기 위해서, policy probability로 주어지는 1/w를 곱해서 reward를 dynamic하게 reweight
- stop-graident operator를 사용해서 reward scaling term w를 통해 gradient가 흐르지 않도록 함
-
식을 좀 더 간단하게 쓰기 위해 정답인 경우(y*)에 대해서만 식을 작성하면 8번이 됨
- 이제 gradient가 흐르지 않기 때문에, 수정된 SFT는 간단한 reweighted loss가 되고, DFT라고 명명

- 하지만 전체 trajectory에 대한 importance weight를 계산하는 것은 수학적으로 불가능하기 때문에, PPO처럼 token-level에서의 importance sampling을 적용
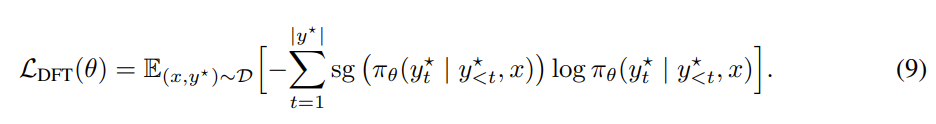
-
DFT에서의 reward는 모든 expert trajectory에 대해서 uniform하게 1이 됨
- 이는 RLVR이 모든 정답 sample에 대해 동일한 reward를 부여하는 것과 비슷
-
결과적으로, 특정 low-probability reference token에 과도하게 집중되는 현상을 피하게 하고, 추가적인 샘플링이나 reward model없이 좀 더 안정적이게 업데이트 하면서 향상된 일반화 성능을 이끔!
-
코드 수정 한 줄만 하면 됨
loss = loss * torch.softmax(shift_logits, dim=-1).gather(1, shift_labels.unsqueeze(-1)).squeeze(-1).detach()
Experiments
Main experiment - SFT setting
-
Setup and Implementation details
-
Dataset
- NuminaMath CoT dataset : 860K, 중국 고등학교 수학 문제와 미국 국제 수학 올림피아드 문제를 포함 ⇒ 여기서 100K sampling해서 학습 데이터로 사용
-
Model
- Qwen2.5-Math-1.5B, Qwen2.5-Math-7B, LLaMA-3.2-3B, LLaMA-3.1-8B, andDeepSeekMath-7B-Base.
-
Training details
-
AdamW optim 사용
-
epoch 1
-
lr은 Llama-3.1-8B만 2e-5, 나머지는 5e-5 사용
-
batch는 256, maximum input length는 2048
-
cosine decay schedule with warm-up ratio 0.1
-
iw-SFT도 포함
- 동기간에 나온 방법론
-
-
Evaluation settings
-
Math500, Minerva Math, OlympiadBench, AIME 2024, AMC 2023 사용
-
모든 모델은 기본적으로 chat template, CoT prompting 사용
-
실험은 16번 decoding run해서 평균, temperature는 0.1, maximum generation length는 4096
-
-
-
Main result
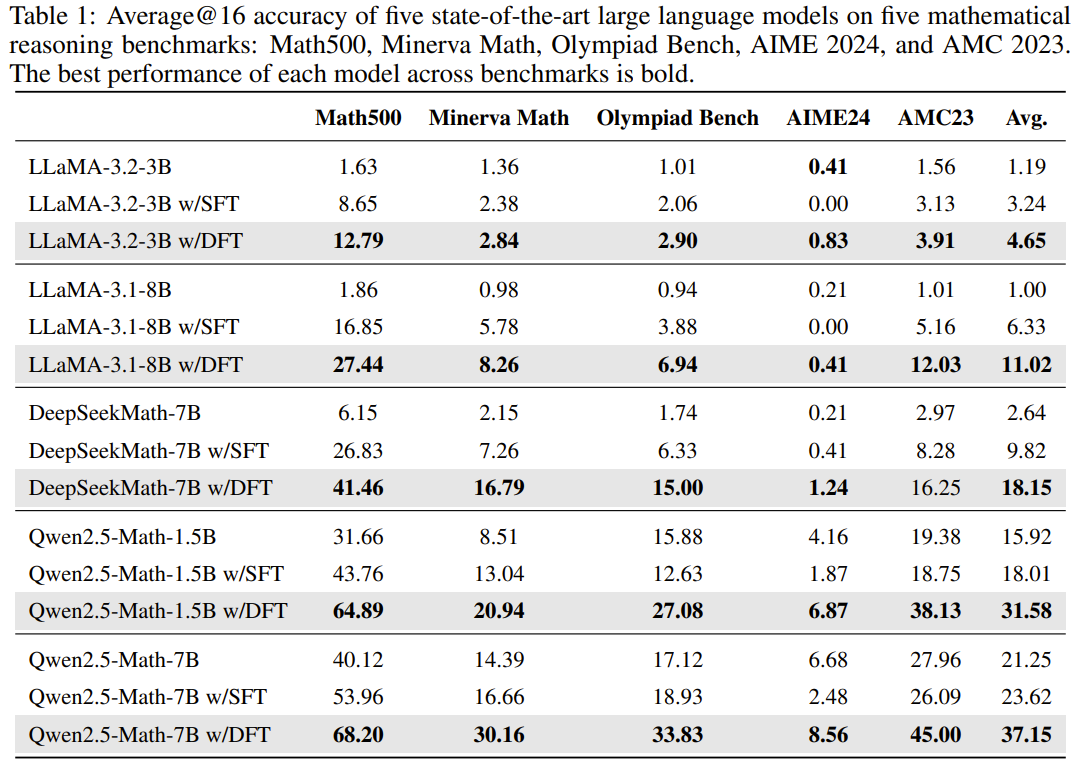
-
DFT는 모든 베이스 모델에 대해서 SFT보다 높은 성능을 보임
-
특히 DFT는 좀 더 어려운 벤치마크에서 강점을 보임 (generalization과 robustness가 뛰어남)
- SFT의 경우 OlympiadBench, AIME24, AMC23과 같은 어려운 데이터셋에서는 base모델보다 낮은 성능을 보이는 경우도 있는 반면, DFT는 이러한 데이터셋에서도 뛰어난 성능을 보임
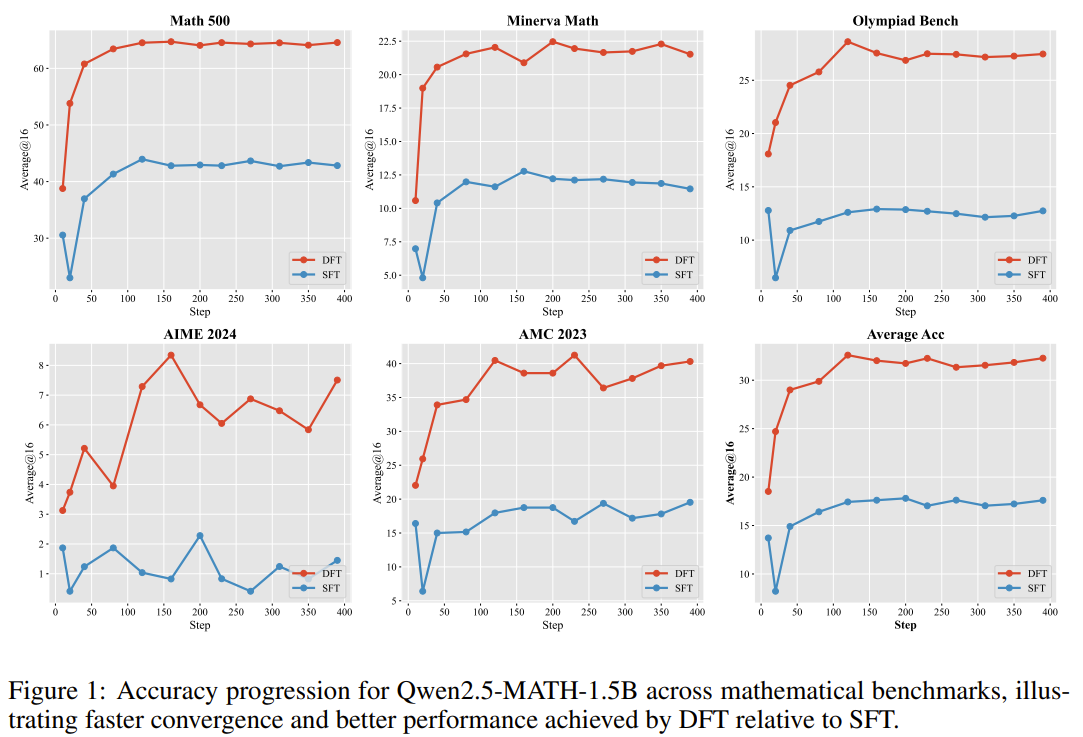
-
DFT는 SFT와 비교했을 때 빠른 수렴 속도, 뛰어난 초기 성능, 높은 샘플 효율성을 보임
- 학습이 수렴되는 속도가 빠르며, 학습 초기 10-20단계만에 SFT의 최종 성능을 뛰어 넘음 + 최고 성능에 도달할 때까지 더 적은 업데이트(=더 적은 학습 데이터)를 필요로 함
-
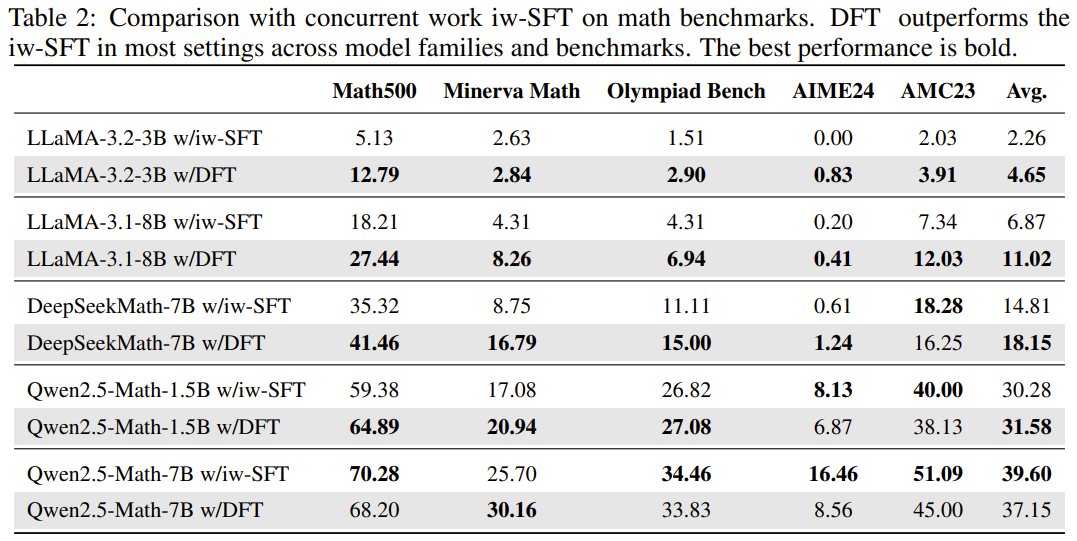
비슷한 시기에 나온 iw-SFT와 성능을 비교해도, 대부분의 경우에서 평균적으로 높은 성능을 보임
- 특히, iw-SFT의 경우 특정 모델이나 벤치마크에서 성능이 불안정
(iw-SFT는 reference model을 써서 reweight하는 방법론)
Exploratory experiment - offline RL setting
-
Data Preparation
-
DFT를 offline setting에 적용해봄
-
SFT setting에 비해서 reward의 sparse문제(확률이 낮은 정답에 너무 집중하는 문제)가 완화될 수 있음
-
데이터는 RFT와 동일하게 함
-
-
rejection sampling fine-tuning (RFT) framework를 위해서 아래와 같은 방식으로 데이터 구축
-
100000개의 math question에 대한 답을 sampling, base model로부터 질문당 4개의 response를 생성
- (논문엔 10000개라고 하는데 그럼 140000개의 데이터가 나올 수가 없을듯.. 오타라고 생각)
-
정답만 학습 데이터로 사용, 거의 140K개의 데이터를 사용
-
-
DPO를 위해서 100K개의 positive-negative preference pair를 구축
-
-
Training details
-
Qwen2.5-math-1.5B model로 실험
-
DFT를 DPO, RFT, PPO, GRPO와 비교
-
RFT와 DFT는 위와 동일한 config 사용
-
DPO는 ms-swift framework를 사용, lr 1e-6, batch size 128, warmup ratio of 0.05
-
PPO와 GRPO는 verl framework에서 학습, lr 1e-6, batch size 256, warmup ratio 0.1
- GRPO에서 group 크기는 4
-
-
Results
-
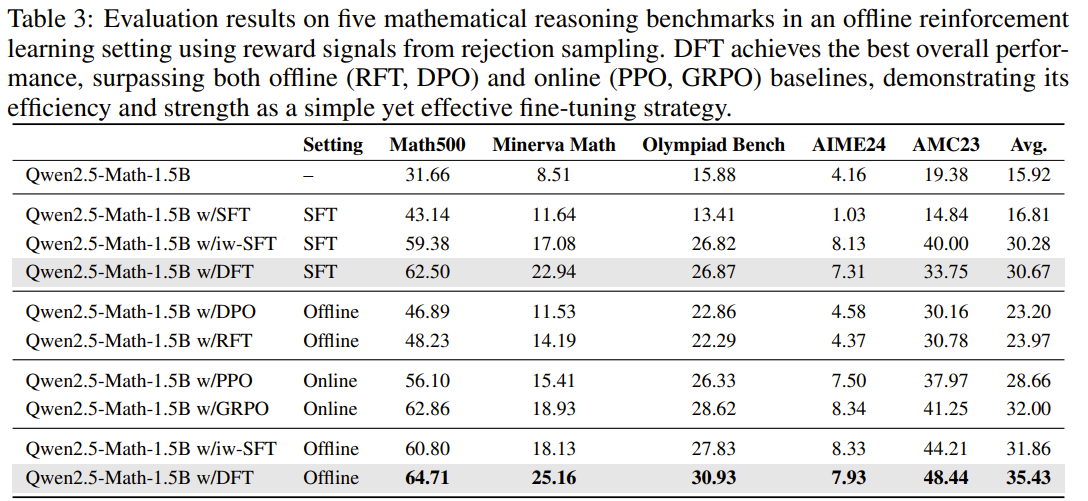
DFT는 SFT setting에서도 offline RL보다 높은 성능을 보임
-
online RL보다는 살짝 밀리지만, DFT를 offline setting으로 하면 online RL보다도 높은 성능을 보임
-
Ablation and investigation
-
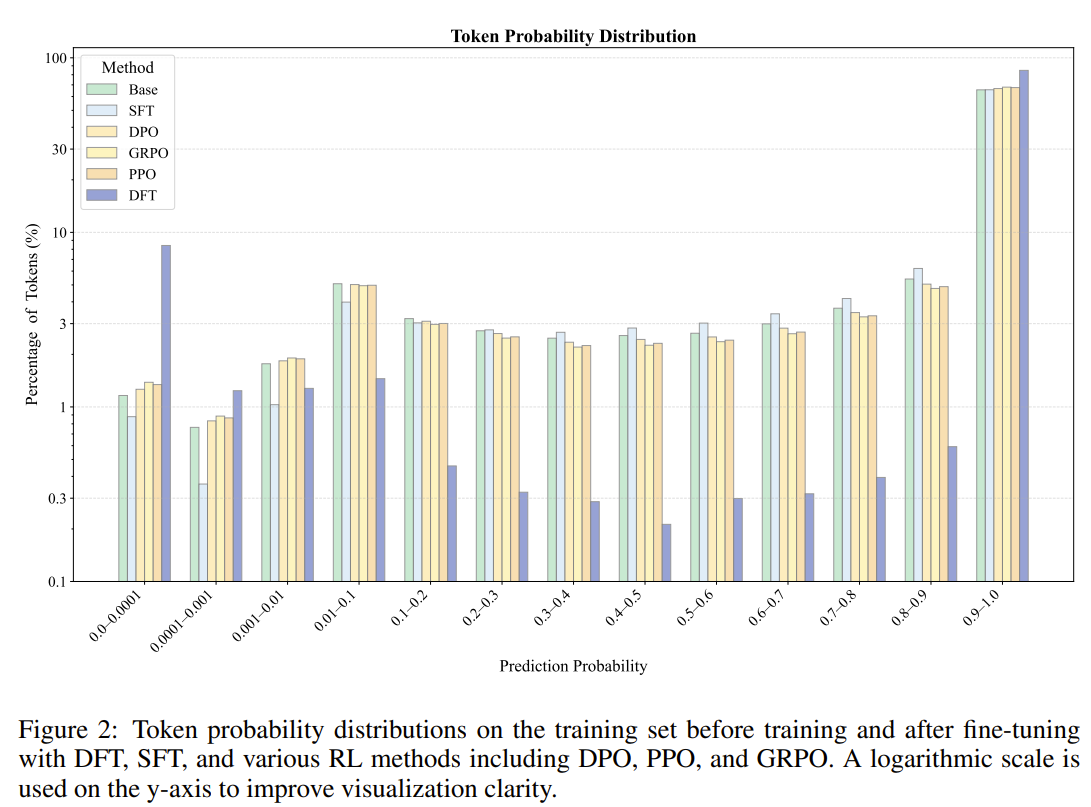
Token probaility distribution
-
SFT는 토큰 확률을 균일하게 증가시키는 경향이 있음
- 하지만 base와의 차이를 보면, 주로 확률이 낮은 토큰들을 조정한다는 것을 볼 수 있음
-
DFT의 경우 일부 토큰들의 확률은 대폭 낮추면서 다른 토큰들의 확률은 높이는 경향 존재(양극화 효과)
-
가장 낮은 확률 구간에 속하는 단어들은 보통 ‘the’, ‘let’, ‘,’, ‘.’ 등과 같은 접속사나 구두점이었음
-
⇒ 견고한 학습을 위해서 모든 토큰을 동일한 신뢰도로 맞추려고 하면 안된다. LLM의 경우 핵심적 의미를 전달하기보다 문법적 기능을 수행하는 토큰들의 학습 우선순위를 낮추는게 유리할 수 있다
- 학생들이 연결어보다는 실질적인 개념에 집중하도록 하는 것과 유사..
-
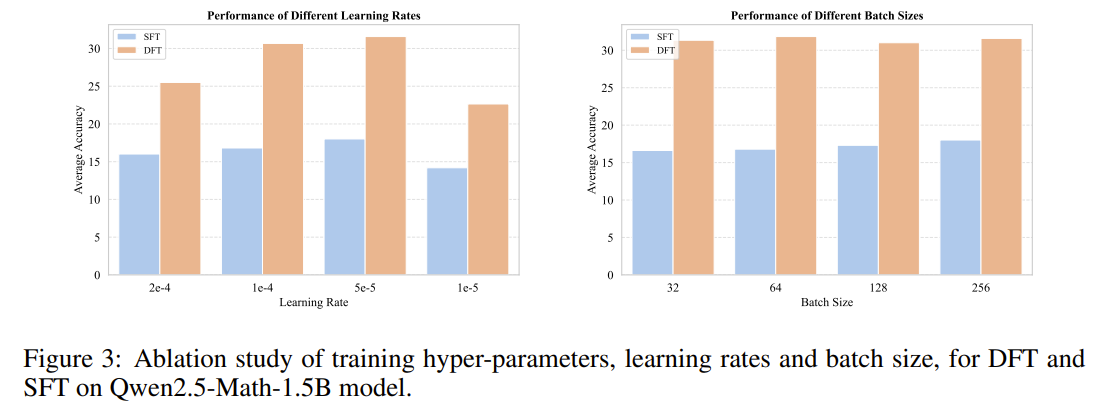
Training hyper-parameters ablation
- lr, batch를 바꿔봐도 DFT 승!
Conclusion
-
SFT식을 조금 reformulate하면 policy gradient의 식처럼 바꿀 수 있음
- 특수한 importance weight가 내재된 policy gradient의 형태
-
SFT에 내재된 imporatence weight의 역수를 loss에 곱해줘서 학습 안정성을 높이면서 성능도 높이는 DFT방법론 제안
-
실험 결과, SFT, SFT 변형식 뿐만 아니라 offline RL보다도 높은 성능을 보임
-
추가적인 cost가 전혀 없다는 측면에서 한번쯤 SFT 대신 loss만 바꿔서 학습해볼만할지도?
- 물론 본 논문에서의 실험은 수학 도메인에만 제한적…
-
계속 이 policy gradient와 SFT사이의 오묘한 느낌.. 비슷하면서 다른듯.. 근데 결국 똑같아 보이는.. 느낌을 갖고 있었는데 좀 해소된거 같아서 좋았다!