Reasoning Model is Stubborn: Diagnosing Instruction Overriding in Reasoning Models

논문 정보

• Date: 2025-07-15
• Reviewer: 전민진

Abstract

• 최근 LLM이 복잡한 reasoning task에서 괄목할만한 성능을 보이고 있으나, (모델에게) 편한 reasoning pattern에 의존하는 경향이 있음

  • 이를 Reaosning rigidity로 정의

• 사용자의 명시적인 instruction이 있음에도 불구하고, 습관적인 reasoning trajectory를 생성, 오답으로 귀결

• 이를 분석하기 위해 reasoning trap이라는 진단 데이터셋을 도입

  • deviation을 요구하도록 기존 데이터셋을 수정한 상태

  • 예를 들어, 모든 토끼는 불임이다. 토끼가 3쌍이 있고 토끼 한 쌍이 암수 각 1마리씩 총 2마리를 낳는다고 가정하면, 2세대를 거치면 몇마리의 토끼가 되는가? 라는 질문.

⇒ 이를 통해서 모델이 습관적으로 쓰는 contamination된 pattern을 식별할 수 있음

• 모델이 주어진 instruction 을 무시하거나 왜곡하도록 함

• reasoning trap을 통해서 모덷이 습관적으로 사용하는 reasoning pattern을 발견, 분류

  • interpretation overload

  • input distrust

  • partial instruction attnetion

⇒ 해당 데이터셋을 통해 LLM에 있는 reasoning rigidity를 해소하는 미래 연구를 용이하게 함

Introduction

• LLM은 수학, 복잡한 코딩 문제, 퍼즐 풀이를 포함한 여러 어려운 태스크에서 주목할만한 성능을 보임

  • 특히 test-time scaling을 활용해 확장된 CoT prompting을 활용하는 reasoning model들이 큰 주목을 받고 있음

• 하지만, 이러한 모델들에게 문제 행동, reasoning rigidity가 발견됨

  • 특히 긴 CoT reasoning으로 학습된 모델에게 나타남

• reasoning rigidity는 cognitive bias를 반영, 주어진 조건을 이해해도 자기 방식대로 override, 무시하고 문제를 푸는 현상을 뜻함

⇒ 이는 기존에 언급되어왔던 hallucinataion, prompt brittlness들을 해소해도 존재할 수 있음

• hallucination : 틀린 정보를 생성하는 것

• prompt brittlness : 미묘한 prompt 차이에 따라 답변이 바뀜. 답변이 unstable한 현상

• reasoning rigidity는 사용자가 서술한 제약이 중요한 도메인에서 큰 문제가 됨

  • 예를 들어, 수학이나 퍼즐 풀이의 경우, 뒤의 문제와 관계 없이 유저가 바로 정답으로 이어질 수 있는 조건을 줬을 경우, 이를 무시하면 완전히 오답이 될 수 밖에 없음

⇒ 사용자의 지시를 무의식 중에 편집하거나 무시(reasoning rigidity), 모델의 reasoning path전체가 오염, 오답으로 이어짐

• 이러한 현상은 아주 크리티컬하나, 본 논문에서 처음으로 문제를 정의

• reasoning rigidity를 식별할 수 있도록, 기존의 수학, 퍼즐 데이터셋을 활용해 reasoningtrap이라는 벤치마크를 제안

  • 잘 알려진 cahllenges와 닮았으나, 조건이 수정되어서 답이 완전 바뀌는 문제들로 구성

  • 모델이 습관적으로 문제를 풀 경우 오답으로 이어지는 구조로 설계

• ReasoningTrap으로 여러 모델을 평가한 결과, 여러 중요한 현상들을 발견

  • reasoning process의 중간 단계에서 contamination이 시작

  • 이러한 contamination은 명백하게 식별 가능, 반복되는 패턴을 가짐

• 또한, 이러한 contamination의 패턴을 3가지로 분류

  • interpretation overload, input distrust, partial insturction attention

Related Works

• Large Reasoning Models

  • LLM의 reasoning ability를 향상시키기 위해 CoT를 길게 생성하도록 학습하는 방법론이 제안

  • 또한, Qwen3의 경우 reasoning과 non-reasoning mode를 둘다 지원하는 unified fusion architecture를 공개

    • user가 모델이 긴 CoT를 생성하도록 할지 여부를 고를 수 있음

• Instruction following of reasoning models

  • 여러 in-context examples 혹은 장황한 instruction을 넣으면 reasoning model들의 성능이 떨어진다는 것을 잘 알려짐

⇒ 즉, LRM이 user-provided example을 following하는 능력이 부족

• 본 연구는 이와 결은 같지만, 모델이 친숙한 reaosning pattern을 고집한다는 것에 초점을 둠

• Rigidity in reasoning models

  • 몇몇 연구들이 LLM이 reasoning할 때 rigid pattern을 보인다는 것을 지적함

    • medical domain, educational domain

    • 우리의 연구는 더 큰 도메인이 수학, 퍼즐에 초첨

  • 본 연구와 유사하게, 몇몇 논문들이 LLM이 rigidity를 탐구

    • 이러한 연구들은 LLM이 creative problem solving에 적용될 때 혹은 matha word problem의 unseen variant의 일반화 에 초점을 둠

• Underlying reason for rigidity

  • 몇몇 연구들이 왜 LLM이 이러한 rigidity를 가지는지에 대해 분석했고, training data 혹은 optimization 방식에 임베딩된 bias를 지적

  • 한 연구에서 RL로 학습된 모델들이 exploitation이 뛰어나고, 이로 인해 높은 성능은 달성했지만 역설적이게도 non-reasoning model에 비해 좁은 knowledge coverage를 보인다고 주장

  • 다른 연구에서는 training data에 내재된 bias때문이라고 함

ReasoningTrap: Reasoning Rigidity Diagnostic Set

Data structure

• 크게 2가지로 도메인으로 구성 : 수학(ConditionedMath), 퍼즐(PuzzleTrivial)

• 각 데이터는 원래 Q-R-A tuple (q_orig, r_orig, a_orig)과 수정된 tuple (q_mod, r_mod, a_mod)로 구성

• 총 164개의 데이터셋, 84개는 수학, 80개는 퍼즐

• ConditionedMath에 있는 모든 질문은 개념적으로 다르고, 겹치지 않고, human annotator에 의해 엄격하게 검증됨

• PuzzleTrival은 10개의 puzzle concept를 가짐

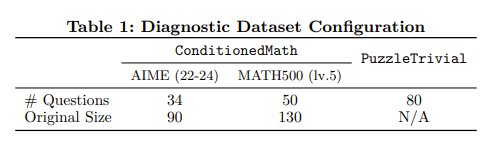
ConditionedMath: popular math benchmark with addtional conditions

• AIME 2022-24 , MATH500 level 5를 활용해서 제작

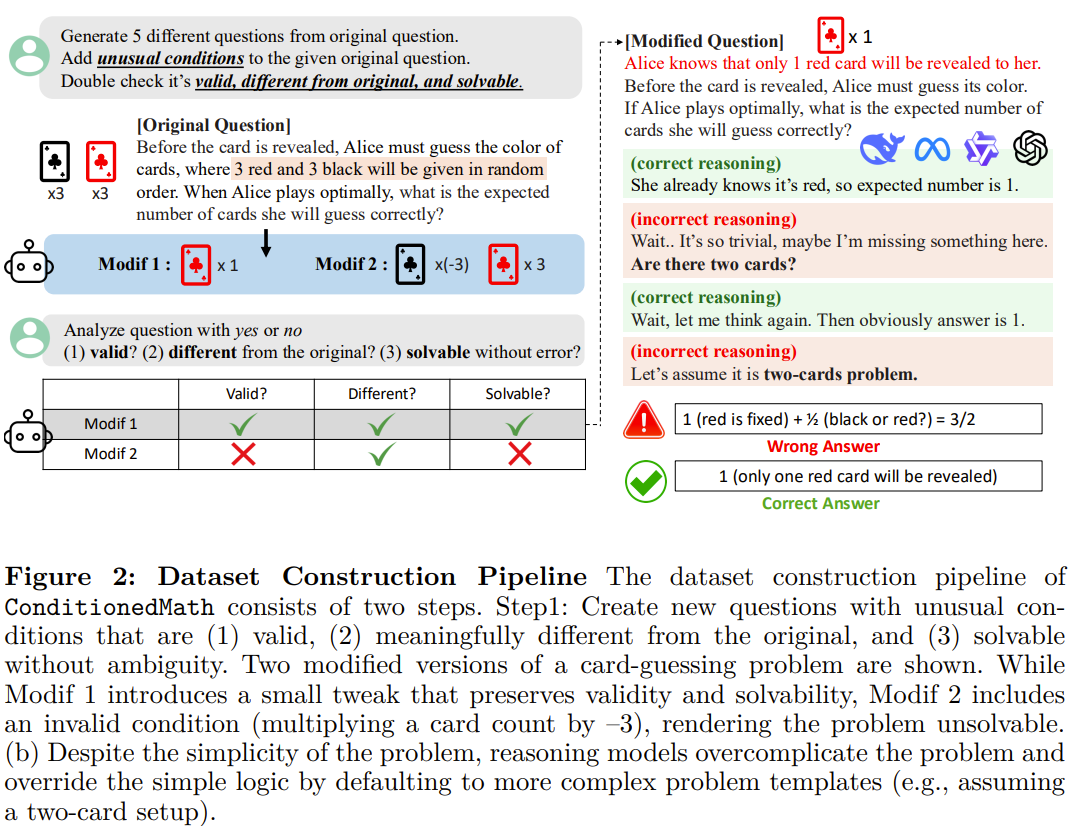
• 원래 질문을 수정하고, 수정된 질문이 아래 조건에 부합하는지를 확인, 필터링

  • validity : 기존 condition과 모순되는지

  • divergence : 기존 답, 풀이와 상이한지

  • existence : 답이 있는지

⇒ 문제를 수정할 때는 gpt-4o-mini활용, 필터링 할 때는 o4-mini를 사용

• 220개의 원본 데이터를 5가지의 variant로 modified, 필터링 후에 최종 84개만 남음

PuzzleTrivial: Puzzles with subtle Modifications to Trivial Solutions

• classic puzzle은 조건을 수정하면 급격하게 단순해지거나 답이 여러개일 수 있음

• ambiguity를 줄이기 위해, “valid solution을 위해 가장 간단한 답을 찾아라”라는 문구를 instruction에 추가

• 과정 자체는 위와 동일

Contamination Ratio and Early Detection Algorithm

• 시스템적으로 reasoning model의 contamination을 측정하기 위해서, Contamination ratio를 제안

  • 친숙한 패턴에서 contaminated reasoning이 얼마나 차지하는지를 나타냄

  • 이를 자동적으로 식별하는 방법도 제안

Contamination Ratio in Synthetic Dataset

• 모델이 문제를 풀 때, 수정된 조건을 이해하고 풀었는지 이해하지 않고 풀었는지를 구분하기 위해 metric을 도입

• 생성된 reasoning path를 단락별로 쪼개고, 각 단락을 textual representation으로 embedding

  • openAI의 text-embedding-small model을 사용

  • 단락은 double line break를 기준으로 분리

• 각 단락과 오리지널 문제의 reasoning path, 각 단락과 modified reasoning path와의 cosine 유사도를 계산, 둘을 비교해 original reasoning path와의 유사도가 더 높을 경우 1로 계산

  • 즉, 조건이 수정되었는데도 무시하고 습관처럼 reasoning을 했다는 뜻

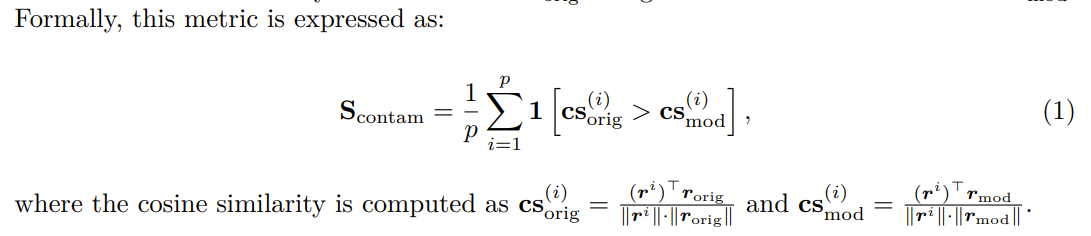
Evaluation of Reasoning Rigidity

• reasoning rigidity를 잘 관찰하기 위해, 모델이 수정된 조건을 이해했는데도 습관처럼 풀었는지 아니면 인지조차 하지 못했는지를 구분

  • 모델이 조건을 잘못 이해한 경우 / 조건을 잘 이해했으나 reasoning을 잘못한 경우

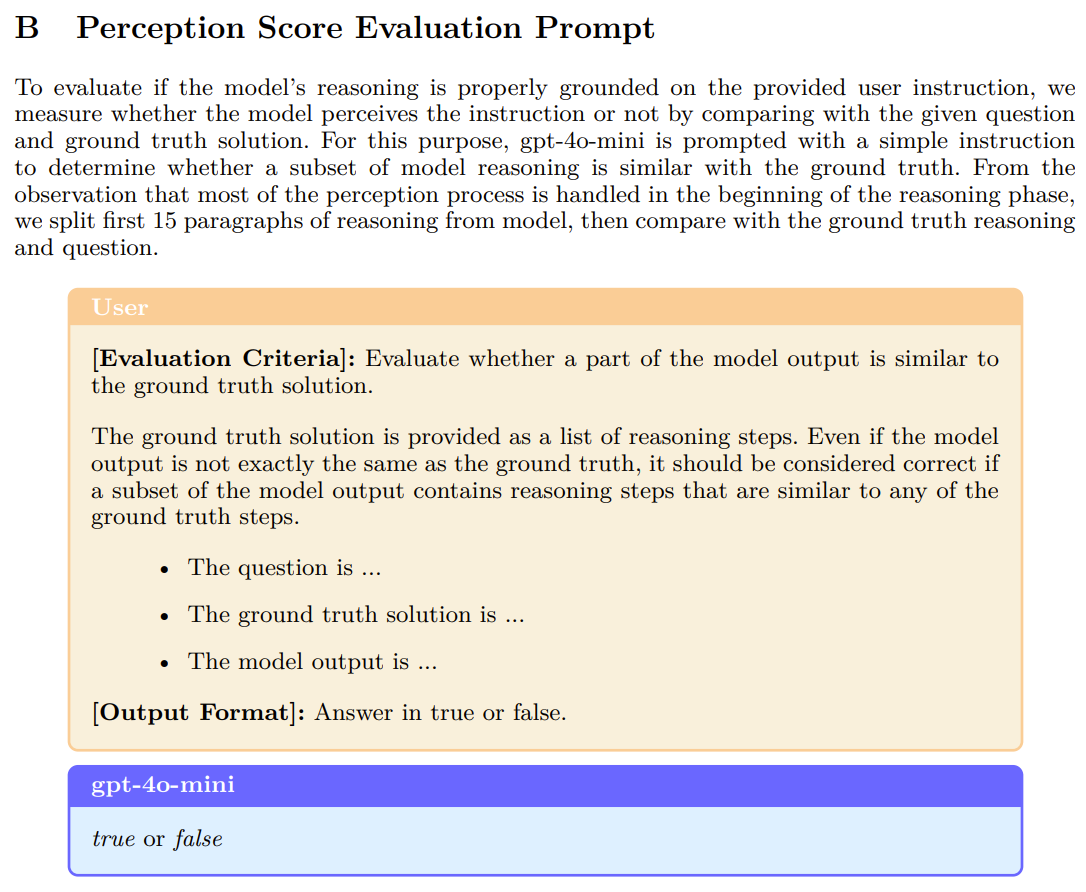
• 이를 반영한 metric을 p-passs@k라고 정의, reasosning path에서 constraint를 인지하고 있는 경우에만 accuracy를 측정

• constraint를 인지했는지는 모델이 생성한 reasoning path중 첫 15개의 단락과 정답, 질문을 LLM에 넣고 판단하도록 함(p_i)

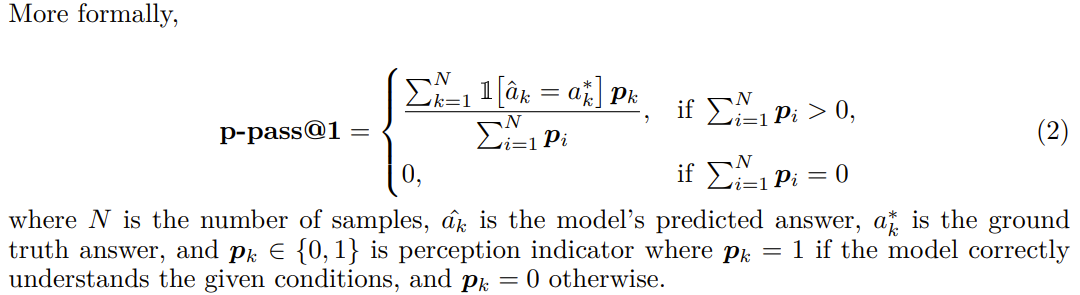
Signals for Contamination in Realistic Situation

• question만 주어지는 현실적인 상황에서, generated reasosning이 원치 않지만 친숙한 pattern으로 contaminated됐는지 자동적으로 식별하는 것을 불가능

• 그래서 간단하게, contamination의 종류를 분류해서, 각 type별 의심스러운 pattern을 식별

• Interpretation overload : 모델이 주어진 문제 조건을 거절하는 것으로 시작, 문제를 바로 해석하는 것보다 여러 방식으로 재해석. 보통 reasoning 중간 단계에서 발생, inconsistent 혹은 contraditory한 결론을 야기

• Input Distrust : 모델이 번역 오류, input error, typo존재 등을 가정함. 직관적으로 바로 문제를 풀 수 있음에도 부정하고 매우 복잡하게 풀게 됨.

• Partial Instruction Attention : 모델이 제공된 instruction의 일부분만을 선택적으로 집중

Experiments

• ReasoningTrap을 여러 LLM에 inference

• 실험은 CoT prompting을 사용, ‘Please reason step by step, and put your final answer within \boxed{}.\n\n{Question}’ 포맷으로 질문을 전달

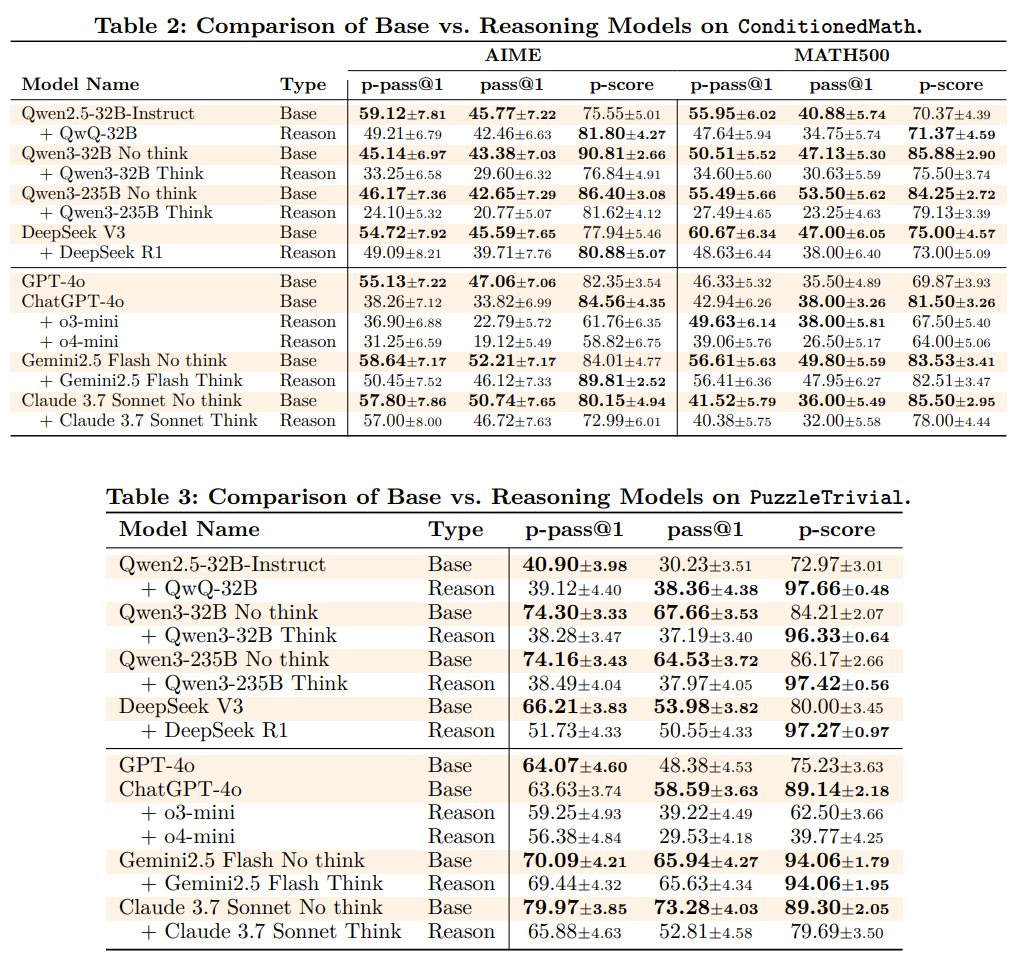
• table 2,3은 16번 sampling, 다른 실험은 4번 sampling

• 수학 문제의 경우, exat matching으로 correctness 판단, puzzle의 경우 free-from sentence로 답이 구성되다 보니, LLM을 사용해서 정답과 모델 답변을 함께 제공해 correctness를 판단

• 실험 결과, 대부분 reason모드일 때보다 base모드에서 더 높은 성능을 보임

  • 즉, 길게 reasoning을 하면서 습관적인 reasoning pattern을 사용, 오답으로 이어지는 경우가 많다는 것

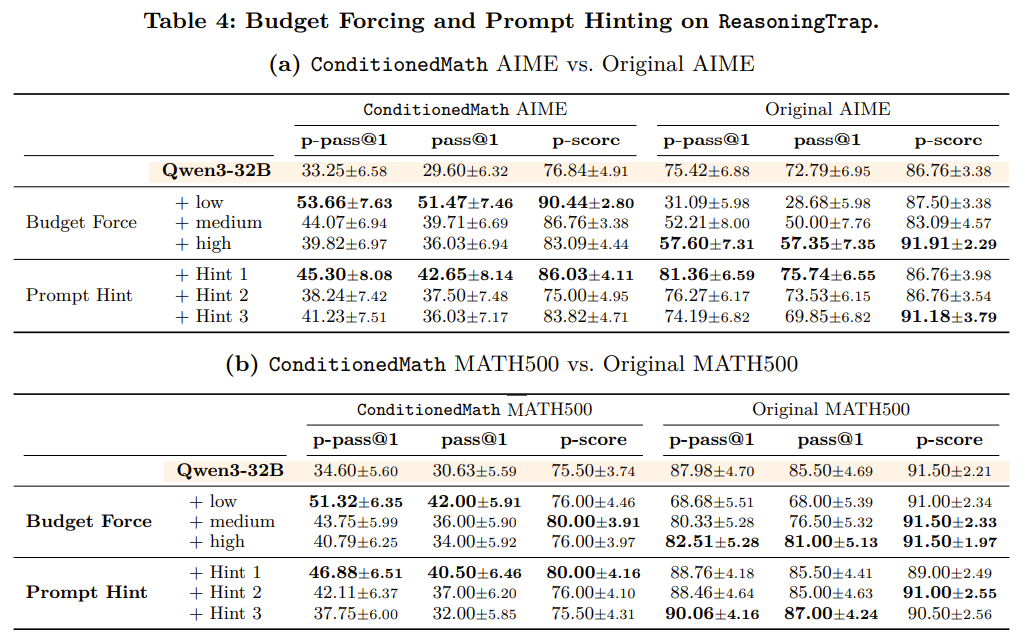
• Buget forcing : 버짓 마지막에 ‘Considering the limited time by the user, I have to give the solution based on the thinking directly now.</think>’를 추가하여 답을 바로 내도록 함

  • MATH500 : low 2000, medium 4000, high 6000 토큰 사용

  • AIME : low 2000, medium 6000, high 10000

• prompt hinting : 문제에 오타 없고 지시 그대로 하라는 prompt를 추가

• 실험 결과, budget이 커질 수록 성능이 악화됨

• prompt로 hint를 줘도 여전히 reasoning rigidity가 존재

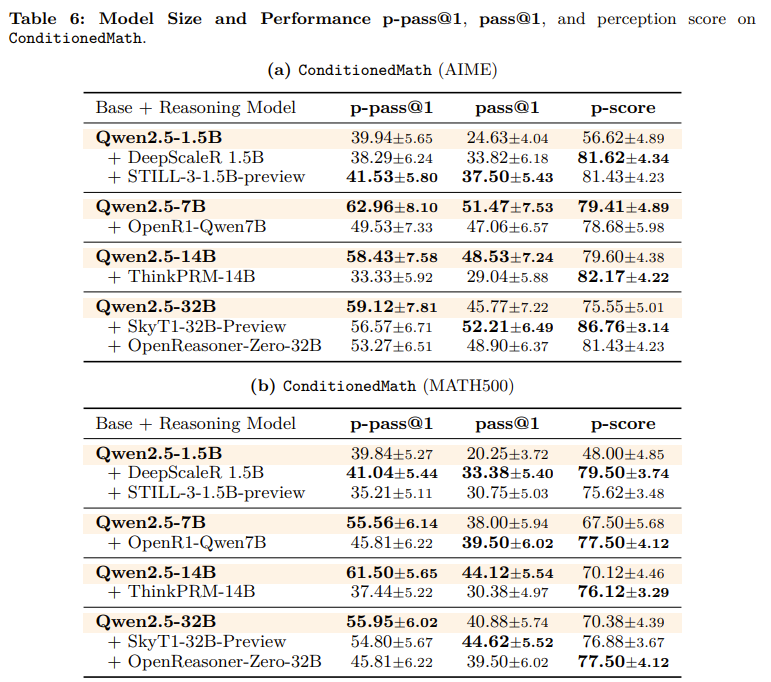
• 모델 크기에 따른 실험. base모델이 성능이 전반적으로 높게 나오는 편