Reasoning Models Can Be Effective Without Thinking
논문 정보
- Date: 2025-07-01
1. Introduction
LLM을 이용해 복잡한 문제를 풀 때, 보통 우리는 “긴 chains of thoughts”를 생성하고 그것을 이용해 reflection, backtracking, self-validation 등을 수행하곤 한다 (“Thinking”). 이러한 reasoning path는 일반적으로 reward를 이용한 강화학습, 혹은 distilled reasoning trace를 이용한 finetuning을 통해서 획득되며, 이 explicit한 reasoning path가 실제로 성능에 많은 도움이 된다고 믿어져왔다. 이 때문에 inference-time compute scaling이 주된 paradigm이기도.
하지만 저자들은 이에 대한 근본적인 질문을 던진다:
- 정말로 explicit Thinking process가 상위 reasoning을 위해 필요한가?
그리고 저자들은 사실 정교한 reasoning path은 그닥 중요하지 않다는 사실을 다양한 실험을 통해서 증명한다.
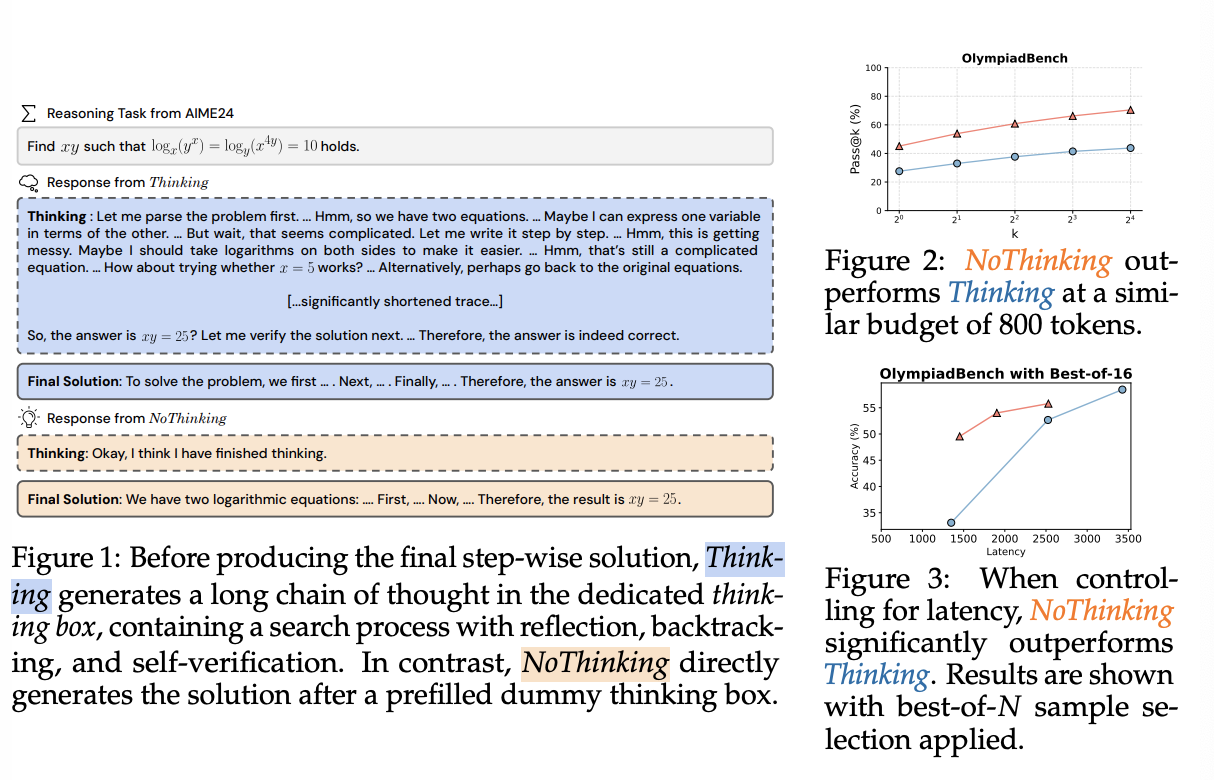
저자들은 DeepSeek-R1-Distill-Qwen을 이용해서 Thinking과 이들이 사용하는 NoThinking — 응답에 가짜 Thinking 블록을 미리 채워 넣고, 모델이 그 이후부터 이어서 답변하도록 하는 방법 — 을 비교해보았을 때, 오히려 NoThinking이 훨씬 더 성능이 좋다는 것을 보인다 (pass@k metrics).
NoThinking은 2.0~5.1배 적은 토큰을 사용하면서도, k=1을 제외하고는 Thinking과 비슷하거나 더 좋은 성능을 보인다.
또한, 두 접근법의 토큰 사용량을 동일하게 통제했을 때, NoThinking은 특히 low-budget 구간에서 pass@1가 Thinking보다 높았으며, k가 커질수록 성능 차이는 더 커졌다 (Figure 2).
효율성을 체계적으로 평가하기 위해 pass@k와 평균 토큰 사용량 간의 Pareto frontier를 분석한 결과, NoThinking은 항상 Thinking보다 우수한 결과를 보였다. 이는 명시적인 추론 과정을 거치지 않더라도 NoThinking이 더 좋은 accuracy-cost tradeoffs를 가진다는 것을 의미한다.
pass@k에서 NoThinking이 좋은 성능을 보였다는 것은, Thinking을 사용한 순차적 추론이 아닌, parallel scaling이 가능하다는 것이다. 저자들은 여러 응답을 병렬로 샘플링하고, best-of-N으로 최종 응답을 고르는 방법론을 제안한다.
이들이 고려한 task는 두 가지이다:
-
tasks with perfect verifiers (e.g., formal theorem proving): 자동으로 정답 여부를 확인할 수 있는 경우
-
tasks without verifiers (e.g., general problem solving): simple confidence-based selection strategies를 사용해야하는 경우
verifiers가 있는 경우, NoThinking이 Thinking을 가뿐히 능가했다 ( both with and without parallel scaling). 특히, 지연 시간을 7배 단축하고 총 토큰 사용량을 4배나 줄였다는 점이 이점. verifiers가 없는 경우에도 NoThinking 준수한 성능을 보인다. 예를 들어, Thinking을 9× lower latency + improved accuracy on OlympiadBench (Math)로 능가함. (Figure 3)
요약하자면, 이 연구는 현재의 추론 모델들이 학습 과정에서 구조화된 추론 형식을 따르도록 훈련되었음에도 불구하고, 높은 성능을 내기 위해 반드시 명시적인 thinking 과정이 필요하지 않다는 사실을 처음으로 보여주고 있다.
또한, NoThinking 방식을 병렬로 처리하면, 순차적 추론보다 더 좋은 latency-accuracy tradeoffs가 가능함을 보인다.
전반적으로, 이 연구는 긴 thinking 과정이 과연 정말로 필요한 것인가에 대한 의문에 대한 답을 일부분 보여주고 있다고 할 수 있다!
2. Related Work and Background
Test-Time Scaling for Language Models
-
Sequential approaches
-
OpenAI o1, DeepSeek R1, Qwen QwQ.
-
긴 chain-of-thought(CoT) 응답을 한 번의 순방향 패스에서 생성하며, 백트래킹과 검증 포함.
-
한계: 강화 학습(RL)이나 iterative self-improvement 등 비용이 큰 학습 과정 필요.
-
-
Parallel approaches
-
여러 후보 출력을 생성하고 선택적으로 응답 집계.
-
ex. Best-of-N 샘플링, search-guided 디코딩 (ex. 몬테카를로 트리 탐색(MCTS))
-
-
NoThinking의 차별점
-
기존 연구는 명시적 thinking이 필수라고 가정했으나, NoThinking은 thinking을 생략해도 됨
-
추가 학습, 보상, 감독 없이 경쟁력 있는 성능
-
Best-of-N을 활용했지만 샘플링 기법 혁신이 아니라 cost-effective baseline for low-budget settings 제공이 목적
-
Efficient Reasoning
recent work has explored various strategies to make reasoning in LLMs more efficient.
-
추론 시퀀스 길이 최적화
- 생성되는 reasoning 시퀀스의 길이를 줄이거나 불필요한 단계를 제거해 간결한 추론을 유도.
-
강화 학습 기반 CoT 최적화
-
강화 학습을 활용해 CoT 길이를 최적화하고 효율적인 reasoning을 학습.
-
ex: 길이에 따라 보상을 설계해 모델이 적절한 길이의 reasoning을 생성하도록 유도 (Aggarwal & Welleck, Luo, Shen, Arora, Qu 등).
-
-
Best-of-N 샘플링을 활용한 파인튜닝
- Best-of-N 방식으로 생성한 다양한 길이의 reasoning을 파인튜닝에 활용해 concise reasoning을 학습.
-
출력 방식 수정으로 reasoning 간결화
- LLM이 reasoning을 latent representations 기반으로 생성하도록 학습해 더 간결한 reasoning을 유도
-
학습 없는 전략적 기준 설정
- 별도의 학습 없이, 프롬프트나 샘플 선택 criteria만으로 추론 전략을 가이드하는 training-free 방식
-
추론 단계 수 제한
- 프롬프트에 토큰 예산을 명시하거나, reasoning 단계를 적게 생성하도록 모델에 직접 지시해 추론을 간결화
-
동적 입력 라우팅으로 reasoning 복잡성 제어
- 입력 데이터를 작업 난이도에 따라 동적으로 라우팅해 복잡성을 조절하고, 쉬운 문제는 간단히 처리하고 어려운 문제만 깊이 추론
3. NoThinking Provides Better Accuracy-budget Tradeoffs than Thinking
Section 3.1: define Thinking and NoThinking
Section 3.2: describe experimental setup
Section 3.3: present experimental results
Section 3.4: Discussions and Analyses
3.1 Method
대부분의 모델들은 보통 비슷한 구조로 generation을 한다:
-
reasoning process within the thinking box, marked by < beginning of thinking > and < end of thinking >, followed by the final answer.
이 구조에 기반해서 Thinking and NoThinking을 다음과 같이 만듦:
-
**Thinking: **the reasoning process within the thinking box, the final solution, and the final answer (Figure 1 (blue)).
-
**NoThinking: ** explicit reasoning process 무시하고 바로 final solution and answer 만들기. thinking box를 decoding 할 때 빈칸으로 하도록 강제 (Figure 1 (orange)).
<|beginning of thinking|>
Okay, I think I have finished thinking.
<|end of thinking|>
| token usage를 제어하기 위해 budget forcing technique from Muennighoff et al. (2025)을 사용 — 모델이 token budget에 도달하면, 강제로 Final Answer 만들도록 함. 만약 아직 thinking box 안에 있었다면, < | end of thinking | > 을 final answer tag 이전에 붙여서 만듬. |
3.2 Evaluation Setup
-
Models
-
DeepSeek-R1-Distill-Qwen-32B
-
Qwen-32B-Instruct
-
(Appendix) R1-series models at smaller scales (7B and 14B)
-
-
Tasks and Benchmarks
-
**Mathematical problem solving: **
-
For standard problem solving: AIME 2024, AIME 2025, and AMC 2023
-
For more advanced reasoning: OlympiadBench
-
-
Coding: LiveCodeBench
-
Formal theorem proving:
-
MiniF2F — for formal mathematical reasoning,
-
ProofNet — for logic and theorem proving.
-
-
-
**Metrics: **pass@k
-
k = {1, 2, 4, 8, 16, 32} for theorem proving datasets (MiniF2F and ProofNet)
-
k = {1, 2, 4, 8, 16, 32, 64} for smaller datasets (AIME24, AIME25, AMC23)
-
k = {1, 2, 4, 8, 16} for larger datasets (OlympiaddBench, LiveCodeBench).
-
for formal theorem-proving benchmarks: pass@32 is the standard
-
for math and coding: pass@1 (i.e., accuracy) is most commonly used.
-
3.3 Results
Thinking vs. NoThinking vs. Qwen Instruct without token budget controlled
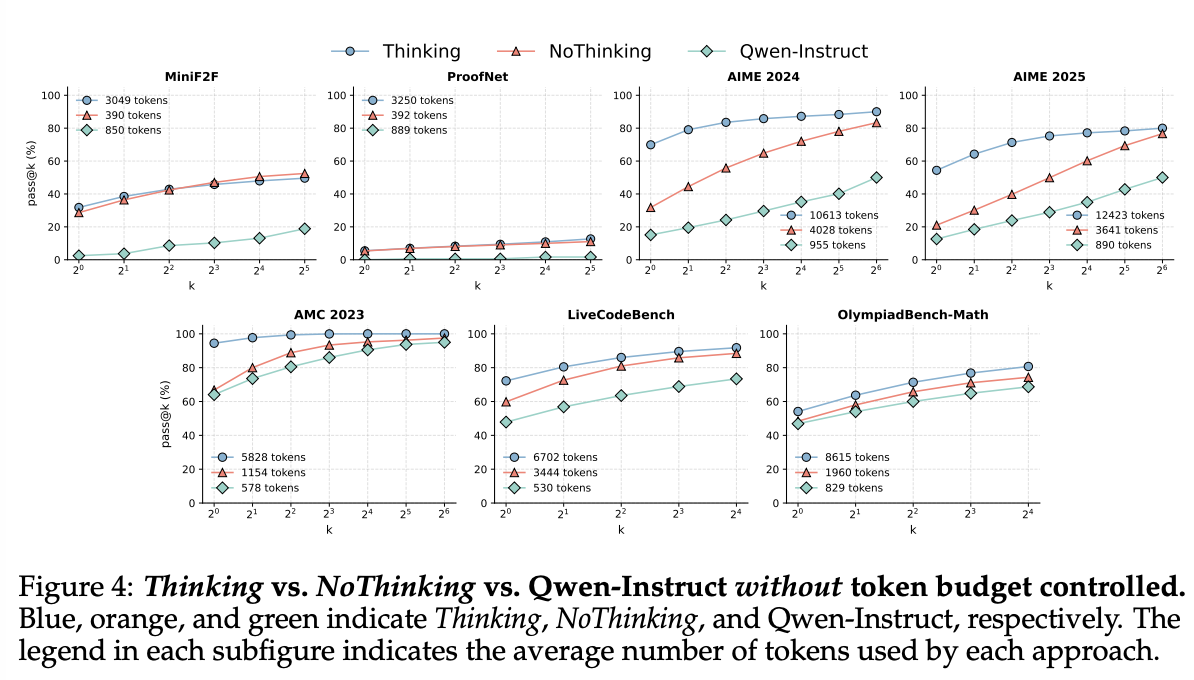
budget forcing없이 세 경우를 비교한 결과:
-
MiniF2F and ProofNet에서 NoThinking은 모든 K에 대해서 Thinking과 비슷했으며, 둘은 Qwen-Instruct보다 성능 훨씬 좋았음
- NoThinking이 3.3–3.7x 더 적은 토큰을 사용하는데도!
-
다른 데이터셋에서는 k = 1일 때는 NoThinking의 성능이 훨씬 떨어지지만, k가 커질수록 갭이 작아짐
-
결과적으로, NoThinking은 가장 큰 k일때, 2.0–5.1x fewer tokens을 사용하는데도, Thinking의 성능을 넘거나 거의 근사함.
-
Qwen-Instruct의 관점에서:
-
For AIME24, AIME25, and LiveCodeBench에서 Thinking and NoThinking이 훨씬 성능 좋음
-
AMC23 and OlympiadBench에서는 Thinking and NoThinking과 비슷
-
Thinking vs. NoThinking with token budget controlled
위에서 확인했듯,Thinking이 NoThinking보다 대부분의 데이터셋에서 성능이 더 좋음. 하지만, 결과적으로 Thinking이 더 많은 토큰을 사용하기 때문에 같은 토큰 수를 사용할 때 어떤 것이 더 성능이 좋은가를 비교함
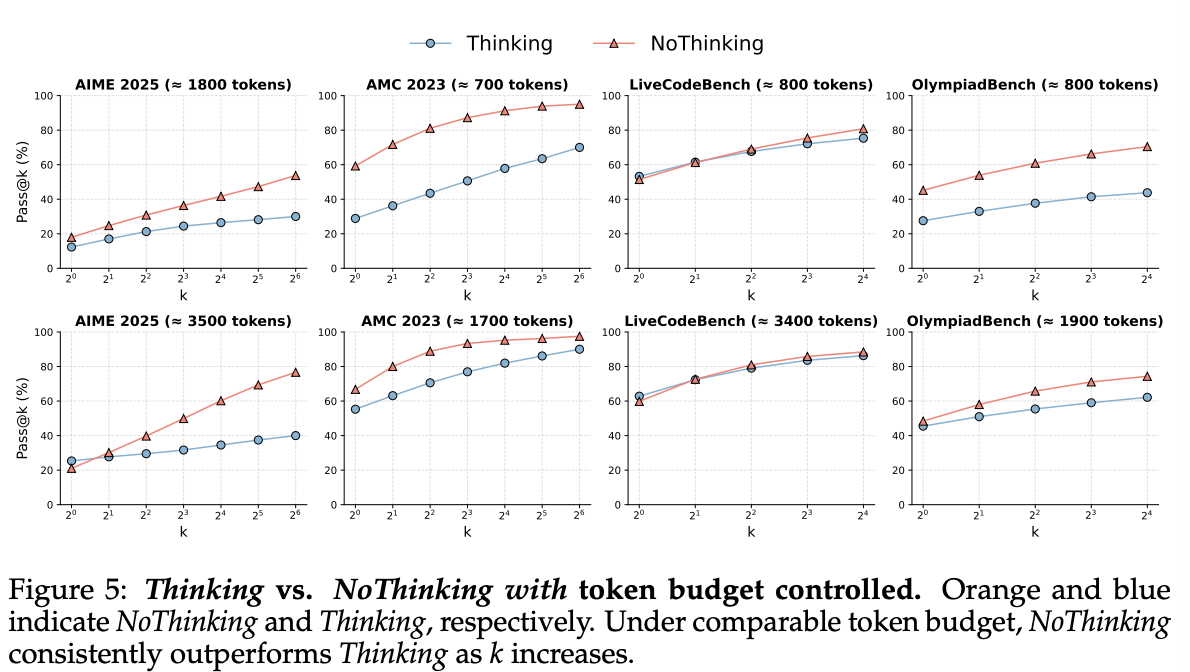
결과적으로 NoThinking generally outperforms Thinking.
특히, low-budget setting (e.g., fewer than ≈ 3, 000 tokens)에서 NoThinking은 모든 k에서 더 좋은 성능을 보였고, k가 커질수록 차이는 커졌음. 좀 더 토큰 제한을 늘렸을 때 (e.g., around 3, 500 tokens), Thinking이 pass@1에서는 더 좋았으나, k = 2부터는 다시 NoThinking이 더 좋은 성능을 보임
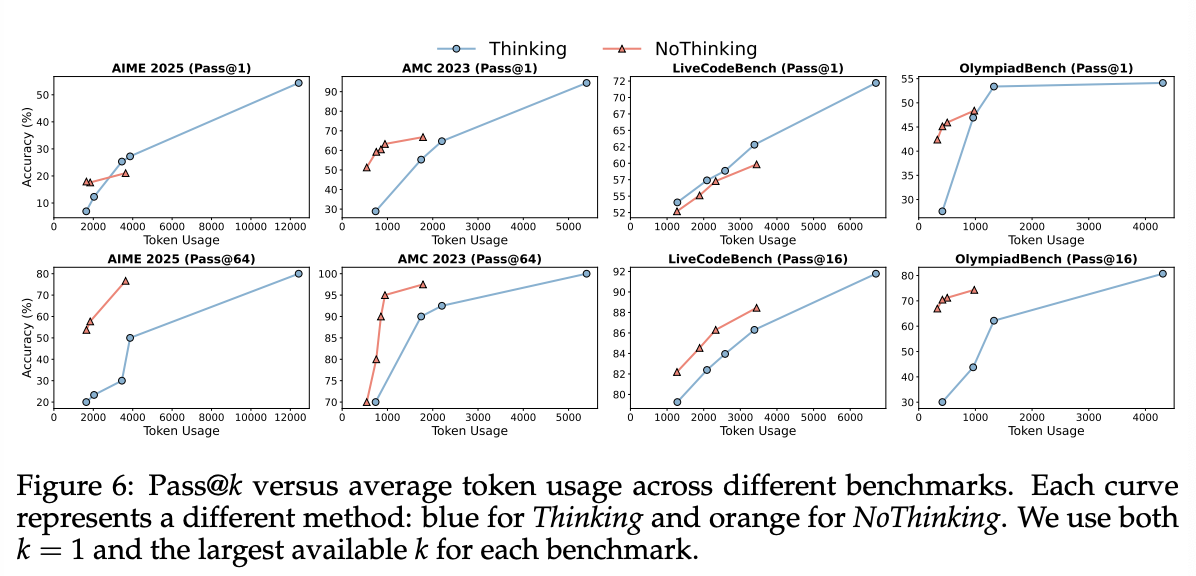
Figure 6는 해당 데이터셋에서 사용한 가장 큰 k와 1, 그리고 token usage를 plot하면서 위의 결과를 더 잘 보여줌.
-
pass@k
- NoThinking이 항상 더 좋았음
-
pass@1
-
NoThinking이 low-budget regime에서는 더 좋고 high-budget regime에서는 더 나빴음
-
LiveCodeBench은 예외. 아마도 thinking box를 없애는 것이 token usage를 그렇게 많이 줄이지 못했기 때문이라고 예상됨
-
data contamination의 위험을 예상하고, 절대 학습에 사용되지 않았을 AIME 2025를 추가함
-
모든 new and established benchmarks의 결과가 이 트렌드가 artifacts of memorization이 아닌, generalizable model behavior임을 보여줌
-
[요약]
-
reasoning models의 핵심인 thinking box를 없애도, 여전히 효과 좋음
-
3.3–3.7x 적은 토큰을 사용하는데도 비슷한 성능 나옴
-
비슷한 수의 토큰이라면 thinking보다 성능 좋음
3.4 Discussions and Analyses
Task-Specific Differences in NoThinking Performance
Section 3.3에서 나름 일관적인 트렌드가 보이긴 하지만, 각 벤치마크 결과를 자세히 살펴보면 조금 동작이 다름
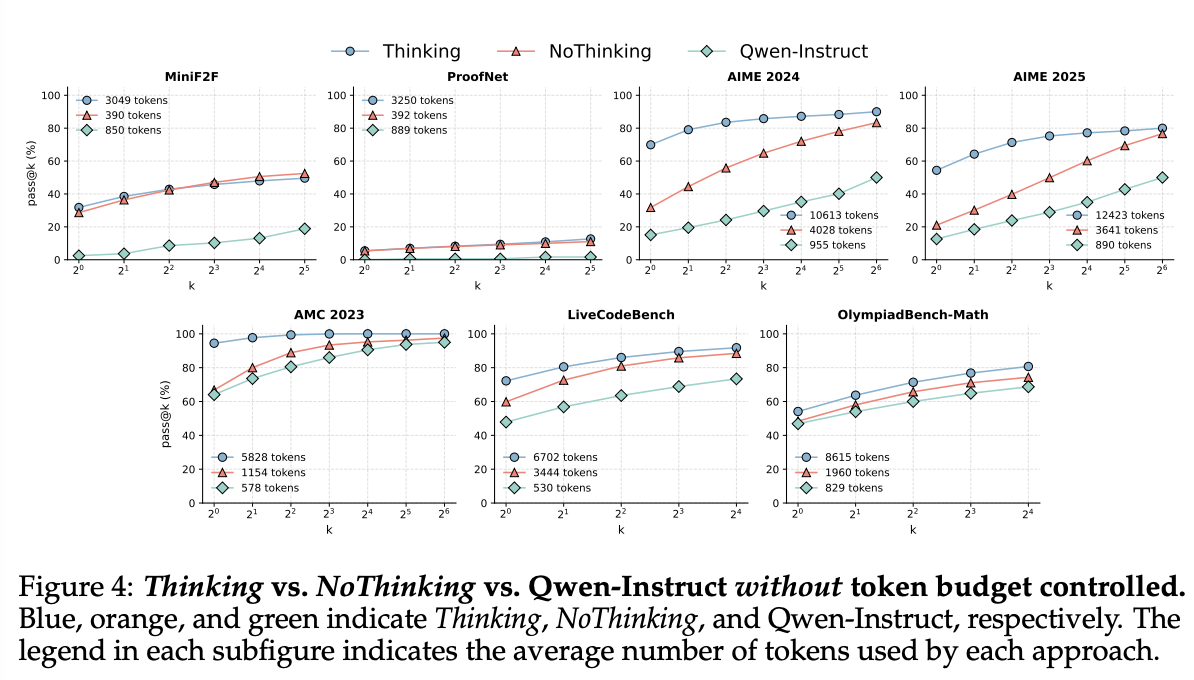
In Figure 4,
-
AMC 2023는 모든 세팅에서 거의 performance gap없이 convergence를 보임. 아마도 saturation이 예상됨
-
MiniF2F and ProofNet pass@1에서 NoThinking은 Thinking에 비해 훨씬 더 적은 토큰을 사용하면서 비슷한 성능을 냄. 하지만, 이는 단순히 task simplicity 이슈로 해석되면 안됨! 검증 결과, OpenAI’s o1과 같은 엄청 강한 모델은 MiniF2F에서 30% accuracy 밖에 안됐고, ProofNet은 모든 방법론에서 성능 낮았음. 즉, 왜 어떤 벤치마크에서는 NoThinking이 잘되었는가는 open question for future work이라는 것
How Increasing k Affects NoThinking Performance
왜 k가 늘어날수록 NoThinking이 더 좋은 성능을 보이는지 대략적인 이유를 찾아보기 위해 생성된 답변의 diversity를 측정함 — by computing the entropy of the answer distribution for each question.
높은 mean entropy는 당연히 더 높은 overall diversity를 의미하고, lower standard deviation은 더 일관적인 것을 의미. 실험은 token budget이 제한된 환경에서 진행
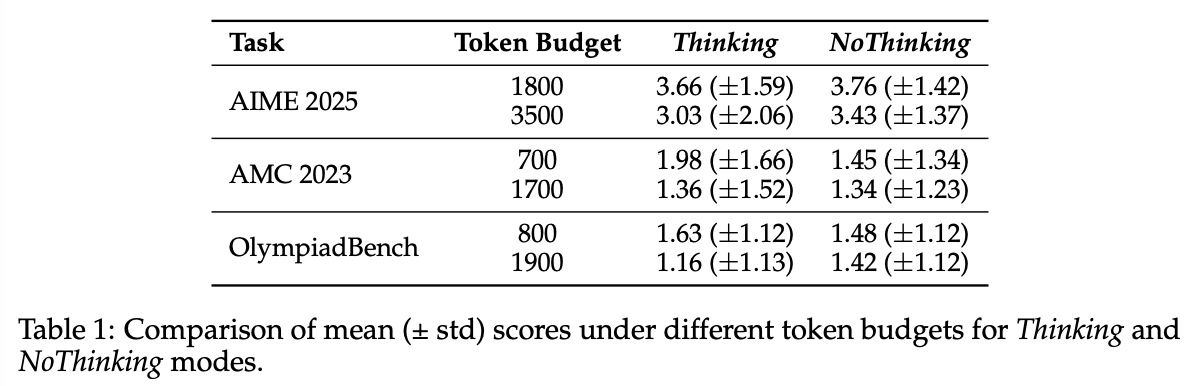
-
엔트로피의 관점에서는 특별한 차이를 찾지 못함. 어떨 땐 NoThinking이 어떨 땐 Thinking이 더 높음
-
variance의 관점에서 NoThinking은 항상 더 낮은 값을 보임 — 더 uniform하게 답을 내고 있다는 것.
이러한 다양성의 일관성 증가가 k가 커질수록 더 좋은 pass@k를 보이는 이유와 연관이 되어있을 것이라 예상은 한다만, 이를 이용해 성능 차이를 완전히 설명하기는 어렵다고언급
4. NoThinking Makes Parallel Test-Time Compute More Effective
우리는 지금까지 NoThinking이 k가 늘어날수록 더 이점이 늘어난다고 이야기함. 즉, NoThinking을 활용하면 parallel scaling method를 더 잘 사용할 수 있다는 것!
Section 4에서는 accuracy vs. latency의 관점에서 어떻게 Thinking보다 더 좋은 세팅을 만들 수 있는지 논한다.
4.1 Motivation and Methods
Parallel Scaling v. Sequential Scaling
-
Parallel scaling:
-
low latency: 여러 샘플을 동시에 생성하므로 지연 시간이 줄어듦 — 이는 API 호출이든 로컬 모델 서비스든 동일함.
-
전체 지연 시간은 가장 오래 걸린 개별 샘플의 생성 시간을 기준으로 측정함.
-
NoThinking은 low-budget 구간에서 더 좋은 성능을 보이고, k가 커질수록 성능이 향상되기 때문에, 단순한 best-of-N 방식을 사용했을 때도 정확도와 지연 시간 측면에서 더 우수한 성능을 달성할 수 있음.
-
실제로 budget forcing과 병렬 샘플링을 적용한 Thinking, 그리고 sequential scaling 하의 full Thinking(Thinking without budget forcing)과 비교했을 때도 NoThinking이 더 나은 성능을 보였음.
-
Methods
-
Parallel sampling
-
병렬 샘플링은 N개의 독립적인 해답을 집계해 단일 예측을 생성하는 best-of-N 방식을 필요로 함.
-
N개의 예측 P = {p₁, ···, pₙ}이 있을 때, best-of-N은 최종 출력을 P 중 하나로 선택함.
-
-
검증 가능한 작업(MiniF2F, ProofNet)
- Lean 컴파일러와 같은 perfect verifier f를 사용해 각 예측 p ∈ P의 정답 여부를 확인하고 최종 정답을 선택함.
-
verifier가 없는 작업
-
**Confidence-based **
-
Kang et al. (2025)를 따라 self-certainty 지표를 사용하여 경량의 confidence 기반 선택 방식을 적용.
-
self-certainty는 예측된 토큰 분포와 균등 분포 간 KL divergence를 계산해 모델의 확신도를 수치화함.
-
예측 집합 P의 self-certainty 점수 c₁, …, cₙ를 계산한 뒤, 동일 연구에서 소개된 Borda voting 방식을 통해 최종 답변 선택.
-
equivalence checking이 불가능한 벤치마크(LiveCodeBench)에서는 self-certainty가 가장 높은 응답을 최종 선택함.
-
-
**Majority voting **
-
정확한 정답이 존재하는 과제(수학 문제 풀이, 과학 문제)에서는 이전 연구를 따라 majority vote 기반의 결과를 보고함.
-
예측 집합 P에서 추출한 답변 모음 {aᵢ}로부터 cons@n = argmaxₐ ∑₁ⁿ 1(aᵢ = a)로 majority vote.
-
k < N인 경우, 전체 N개 예측에서 무작위로 k개를 샘플링해 컨센를 계산하고, Monte Carlo simulation으로 여러 번 반복해 정확도를 평균하여 cons@k를 추정함.
-
-
-
Metrics
- 지연 시간(latency)은 각 데이터셋과 N회 반복 실험에서 생성된 토큰 수의 최댓값을 평균하여 정의함.
4.2 Results
-
Tasks without verifiers
-
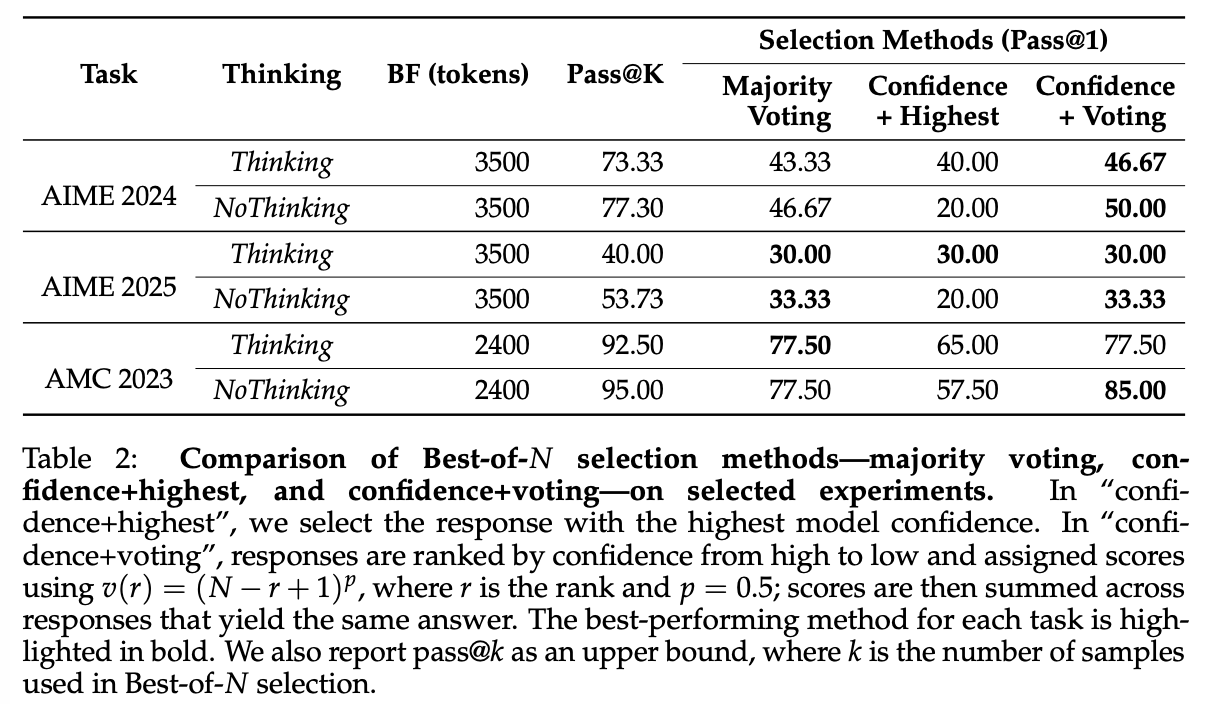
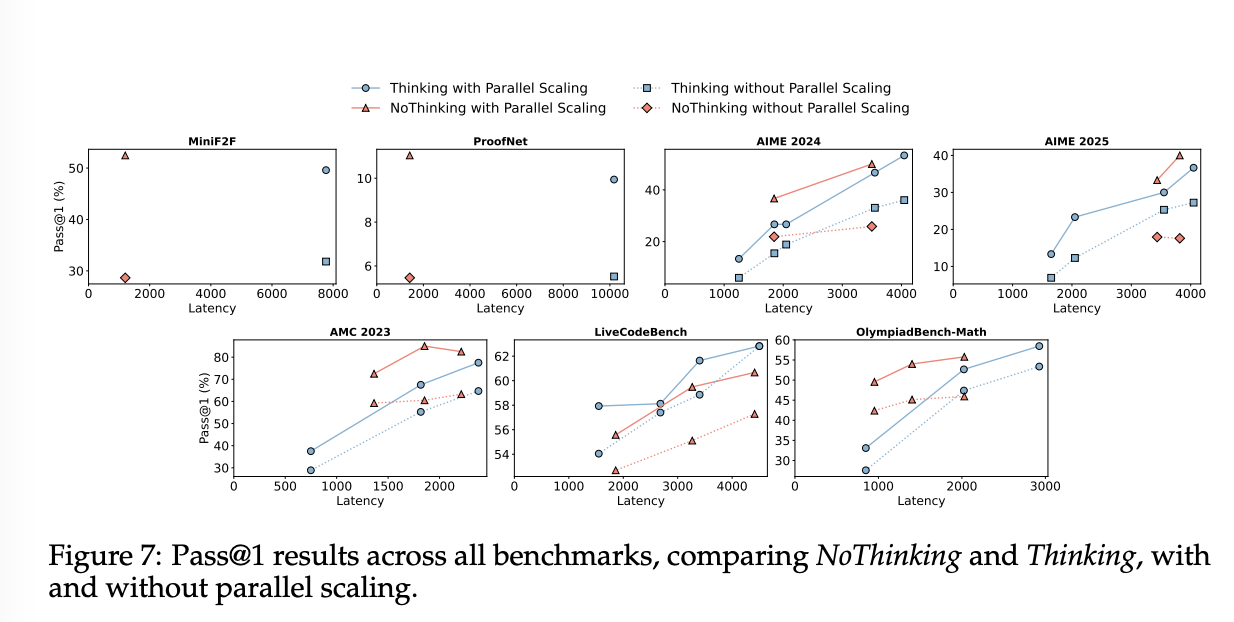
Figure 7에서는 confidence-based 방식을 사용한 결과를 시각화했고, Table 2에는 선택된 실험의 ablation 결과를 제시함.
-
Table 2에서는 Section 4.1에서 논의한 Best-of-N 방법을 비교했으며, 전반적으로 confidence-based 선택이 majority voting보다 더 우수한 성능을 보임.
-
병렬 스케일링을 활용할 경우, 샘플 중 가장 좋은 예측을 선택해 pass@k 성능을 달성할 수 있으므로 pass@k 정확도를 pass@1의 상한으로 보고 Table 2에 포함.
-
-
Perfect Verifiers
-
병렬 스케일링과 결합한 NoThinking은 기존 sequential 접근법에 비해 훨씬 낮은 지연 시간+토큰 수로 유사하거나 더 나은 정확도를 달성.
-
Figure 7의 첫 두 플롯에서 보듯 NoThinking은 Thinking과 동등하거나 더 나은 성능을 보이면서도 지연 시간이 훨씬 낮음.
-
병렬 스케일링 없이도 NoThinking은 Thinking과 비슷한 정확도를 훨씬 짧은 지연 시간으로 달성함.
-
병렬 스케일링과 결합할 때, NoThinking은 budget forcing과 병렬 스케일링 없이 수행한 Thinking과 유사한 정확도를 유지하면서 지연 시간을 7배 줄임.
-
특히 MiniF2F와 ProofNet 데이터셋에서 NoThinking은 출력 토큰 수를 4배 줄이면서도 같은 정확도를 달성함.
-
-
**Simple Best-of-N Methods **
-
NoThinking은 병렬 스케일링과 confidence-based 선택을 결합했을 때, 대부분의 벤치마크에서 Thinking을 일관되게 능가함.
-
Figure 7의 마지막 다섯 플롯은 여러 벤치마크에서 토큰 사용량을 통제한 상황에서 Thinking과 NoThinking의 confidence-based 선택 결과를 보여줌.
-
연구는 주로 low-budget 환경에 초점을 맞추었음. 이유는
-
효율적인 추론에 대한 주된 관심사와 부합하고,
-
최대 토큰 수가 너무 크면 지나치게 길고 비논리적인 출력(“babbling”)이 발생해 비교 가치가 떨어지고 지연 시간만 증가하기 때문.
-
-
병렬 스케일링 자체는 Thinking과 NoThinking 모두에서 pass@1 성능을 개선하지만, 모든 수학 벤치마크에서 NoThinking은 Thinking보다 항상 더 좋은 accuracy–budget tradeoffs를 가짐
-
특히 예산 제한이 없는 full Thinking과 비교해도, NoThinking은 더 높은 pass@1 점수(55.79 vs. 54.1)를 기록하면서 지연 시간을 9배 단축함.
-
-
**LiveCodeBench **
-
NoThinking은 LiveCodeBench에서 less effective: 이는 confidence-based 선택이 정확한 일치 기준이 필요한 코딩 작업에서는 한계가 있기 때문으로 보임.
-
이 경우 정확한 일치 기반 투표가 불가능해 self-certainty가 가장 높은 응답을 선택했는데, 이는 신뢰도가 낮아 성능이 떨어짐.
-
Table 2에 따르면 이러한 방식은 투표 기반 방법이 가능한 다른 작업들과 비교해 일관되게 낮은 성능을 보임.
-
[요약]
-
NoThinking의 pass@k 성능은 k가 증가할수록 더욱 좋아지며, 병렬 스케일링을 통해 pass@1 성능을 유사하거나 훨씬 더 낮은 지연 시간(최대 9배 감소)으로 달성할 수 있음.
-
Verifiers가 있는 작업에서는 정확도는 비슷하거나 더 높이면서 총 토큰 사용량을 최대 4배까지 줄일 수 있음.
Conclusion
-
이 연구는 동일한 모델이 긴 thinking chain 없이도, k가 증가함에 따라 pass@k에서 Thinking 방식과 동등하거나 더 나은 성능을 훨씬 적은 토큰으로 달성할 수 있음을 보여줌
-
동일한 토큰 예산 하에서도, NoThinking은 대부분의 k 값에서 기존 Thinking 결과를 지속적으로 능가함.
-
NoThinking을 Best-of-N 선택 방법과 결합하면, 기존 Thinking 방식으로는 달성하기 어려운 accuracy–budget tradeoffs 달성!