SSM → HIPPO → LSSL → S4 → Mamba → Mamba2
논문 정보
- Date: 2025-02-04
- Reviewer: hyowon Cho
구글에서 공개된 titans가 뜨거운 감자네요. 리뷰를 하려고 열어봤는데, 이미 준원이가 찜해놓기도 하고 + State space model에 대한 사전 지식이 저에게는 부족해서.. 해당 논문에서 주되게 언급되는 Mamba&Mamba2 연구를 가져왔습니다! titans를 향한 여정으로 받아들여주시면 좋을 듯 합니당.
BackGround
Google titans 모델이 등장하자마자 뜨거운 관심을 모으고 있습니다. 가장 큰 특징이라고 한다면, 헤게모니 아키텍쳐인 transformer가 아닌 sequential modeling을 베이스로 하는 아키텍쳐를 사용해서 transformer에 준하는 성능을 내고 있다는 것입니다.
이러한 관점이 titans에서 처음으로 시작된 것은 아닙니다. titans 이전에 State Space Model(SSM)을 활용한 mamba 모델이 sequential modeling의 주류를 차지하고 있었습니다. (titans에서도 mamba-based model들을 주 baseline 모델로 언급합니다)
[State Space Model 기반의 efficient architecture 의 계보]
HIPPO → LSSL → S4 → Mamba → Mamba2 → Samba, …
개인적으로 대단한 것은 HIPPO부터 Mamba2까지 모두 CMU에 계신 Albert Gu 교수님이 모두 1저자로 작성하셨다는 것입니다. 따라서, 해당 흐름을 좇다보면 Albert Gu가 어떠한 아이디어를 기반으로 어떠한 한계를 해결하고자했는지 이해하기 용이할 것입니다.
따라서, 본 발표에서는 SSM의 개념을 소개하고, HIPPO부터 Mamba2까지 Albert Gu 교수님의 머릿속을 탐방해보는 시간을 가지도록 하겠습니다.
SSM으로 대표되는 sequential model들을 설명하기 이전에 먼저, 왜 transformer 이외의 아키텍쳐 연구가 필요한지 알아보겠습니다.
왜 Transformer 이외의 아키텍쳐가 필요한가
기존 Transformer의 문제점: Inference Cost
Transformer는 Attention 메커니즘은 다음과 같은 특징을 가집니다:
-
Attention은 근본적으로 전체 시퀀스에 대한 정보를 축약해 전달받는 것이 아닌, 각각의 정보에 알아서 접근하는 시스템. 따라서, 이전 time-step에 대한 모델의 예측값은 다음 time-stpe의 모델의 예측 값과 상관없음
-
Training
- 한번의 forward로 모든 time-step에 대한 훈련이 가능하기에_ 빠른 훈련! _
-
Inference
-
학습 자체는 빠르게 진행되나, inference 시에도 불필요한 정보들에 모두 attend하기 때문에 메모리+속도 이슈 발생
-
시퀀스 길이에 따라 계산 복잡도가 Quadratic하게 증가하여, 긴 시퀀스 데이터를 다룰 때 매우 비효율적
-
inference시 하나의 토큰을 생성하는데 걸리는 시간이 linear하게 늘어남 + attend해야하는 state의 수 또한 Linear하게 늘어남
-
-
이러한 문제를 해결하기 위해 많은 연구자들이 Linear Attention과 같은 다양한 방법을 제안했지만, 대부분은Transformer만큼의 성능을 내지 못했습니다. 또한, Streaming LLM과 같은 방식으로 inference cost를 낮추기 위한 연구들도 다양하게 존재하지만, 근본적인 해결이 되지는 않았죠.
대항마: Sequential Models
연구자들은 다시 Recurrent model들을 살펴보기 시작합니다. Transformer가 Recurrent 모델의 대안으로 등장한 만큼, 둘은 상반된 장점과 단점을 가집니다.
Recurrent model들은 모두 알다시피 학습 속도가 매우 느리고, 한정된 공간에 정보를 저장하다보니 해당 지식을 유지하는데 문제가 있습니다:
-
하나하나 보기보다는 한정된 메모리에 시퀀스 정보를 잘 모아놓는 방식. 이전 t-1에 대한 메모리가 t의 입력으로 필요함
-
Training
- sequential → slow training
-
Inference
- 그러나, 출력값이 이전 시점의 메모리와 현재의 입력에만 의존하기에(선형적), 토큰 당 생성 속도 및 VRAM 요구치가 constant하다는 장점
즉, Recurrent 모델이 transformer의 대항마로써 인정받기 위해서는 다음의 두 가지 문제를 해결해야 합니다.
-
**‘어떻게 한정된 공간 안에 정보를 잘 집어넣어 성능을 transformer만큼 유지할 것인가’ **
-
데이터의 시간적 연속성(time continuity)을 유지하면서도 이를 효과적으로 처리할 수 있는 모델
-
학습 과정에서 발생하는 Vanishing Gradient 문제를 해결
-
‘**어떻게 학습 속도를 빠르게 만들 것인가’**
그리고 이 두 가지를 해결할 수 있는 실마리가 바로 다음과 같습니다:
-
한정된 공간 내 지식 압축→ Structured SSM
-
훈련 속도 → Parallel Scan
그렇다면 Structured SSM이 무엇인지 알아보기 위해 SSM이 무엇인지부터 개념을 잡아봅시다
State Space Model (SSM)
Overview
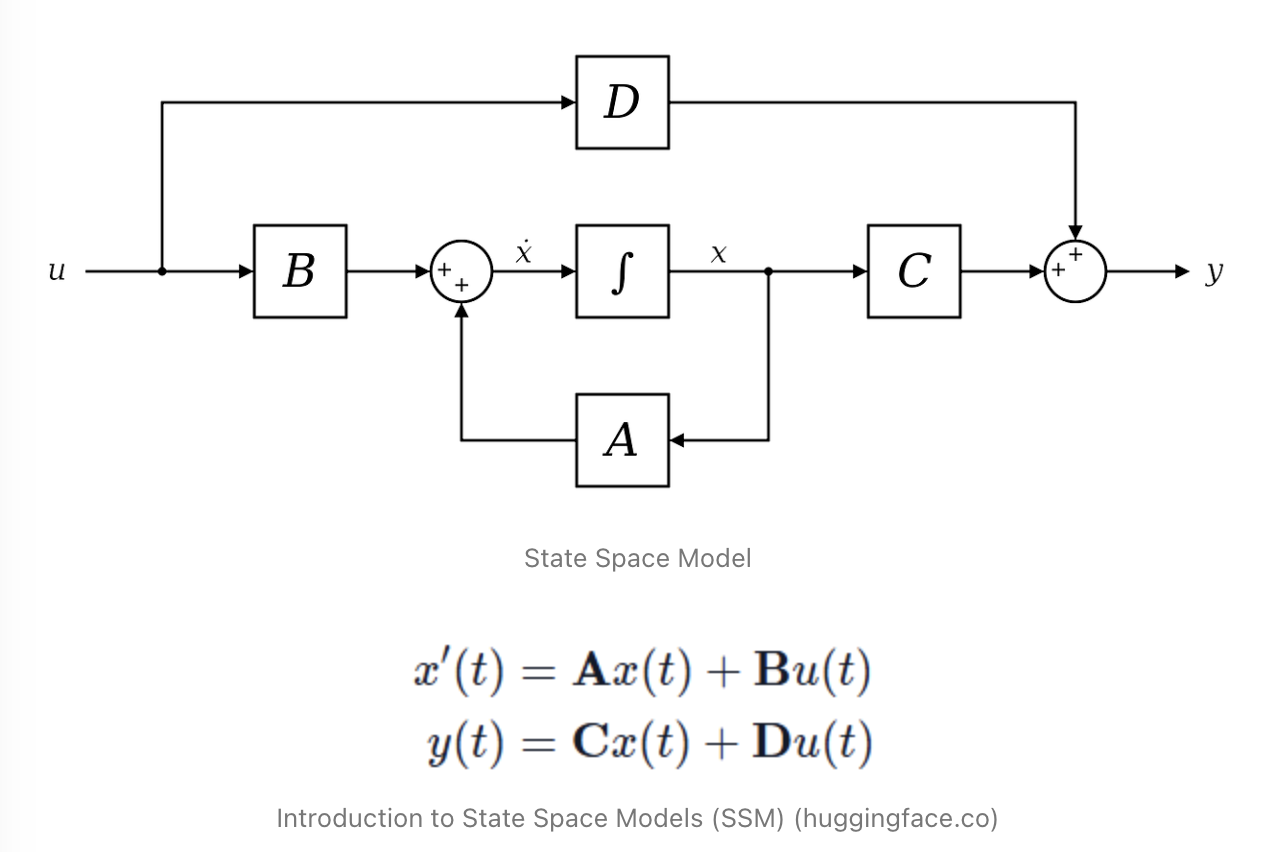
State Space Model(SSM)은 본래 제어 이론에서 유래한 모델로, 시스템의 상태(state)와 출력을 수학적으로 정의한 것입니다.
해당 모델은 연속적인 시간 흐름에 따라 시스템의 상태를 모델링합니다. 즉, (1) 시간에 따라 결정되는 함수와 (2) 0번째 시점부터 t-1번째까지의 입력이 주어질 때, t번째의 출력을 예측하기 위한 시스템이라고 보시면 됩니다.
이 모델은 입력 데이터(x)를 받아 상태(h)를 계산한 후 이를 출력(y)으로 변환하는 위의 두 가지 주요 방정식으로 정의됩니다.
이때 A와 B는 연속적 시스템을 표현하는 중요한 매트릭스들로, 시간에 따른 시스템의 상태 변화를 기술합니다.
-
A: 상태 변화를 결정하는 매트릭스. 이전 상태 Xt−1에 곱해져서 시스템의 상태가 어떻게 변하는지 정의합니다.
-
B: 입력을 상태로 변환하는 매트릭스. 입력 Ut를 받아 상태에 반영하는 역할을 합니다.
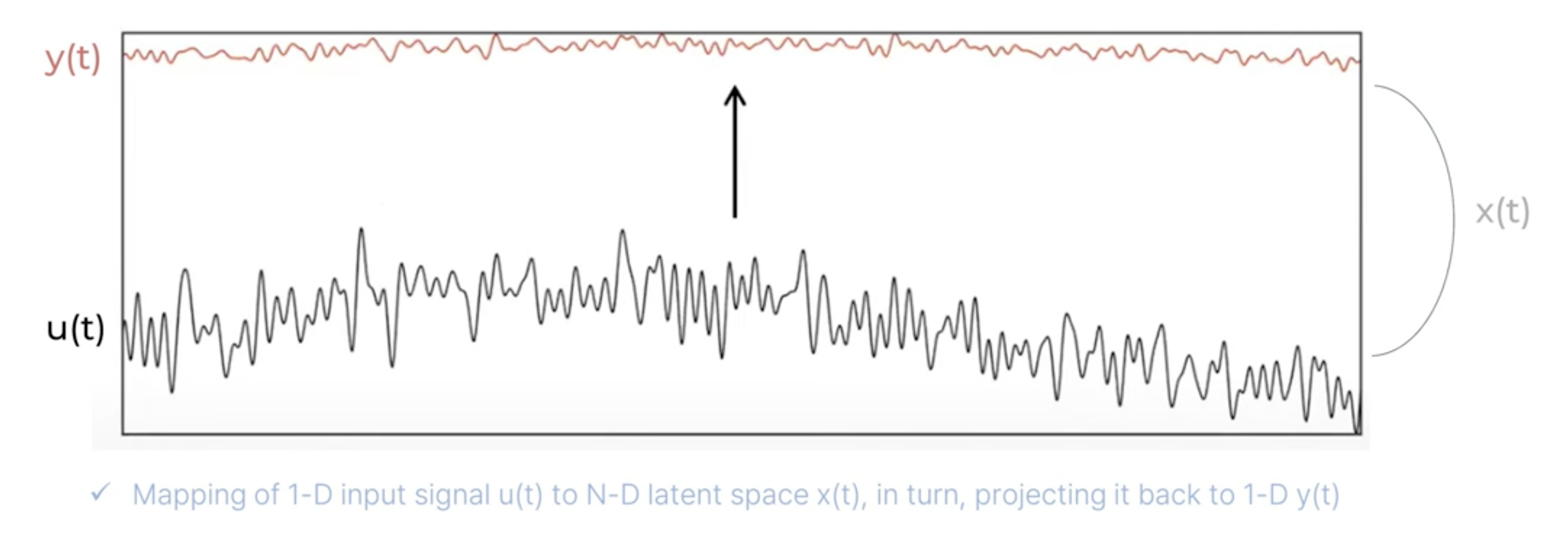
입력 u(t)와 출력 y(t) 사이를 이어주는 latent space의 feature x(t) (hidden vector)를 구하자!
즉, SSM은 시스템의 입력을 고차원의 잠재 공간(latent space)으로 변환하여 처리하는 방식으로 동작합니다.
Details
즉, 우리가 구하고자 하는 것은 latent space의 feature x(t) (hidden vector)인 state. state는 다음과 같이 정의된다:
- state
어떤 시점(t=t0)에서의 변수를 알고, 시간이 지난 어느 시점 (t≥t0)에서의 입력을 알아, 입력이 주어진 시점(t≥t0)에서의 시스템의 거동을 완전히 결정할 수 있을 때, 이러한 변수(상태변수)들의 최소집합 h(t) (용어 혼용 주의: 위에서의 x(t))
Minimum set of variables, known as state variables, that fully describe the system and its response to any given set of inputs
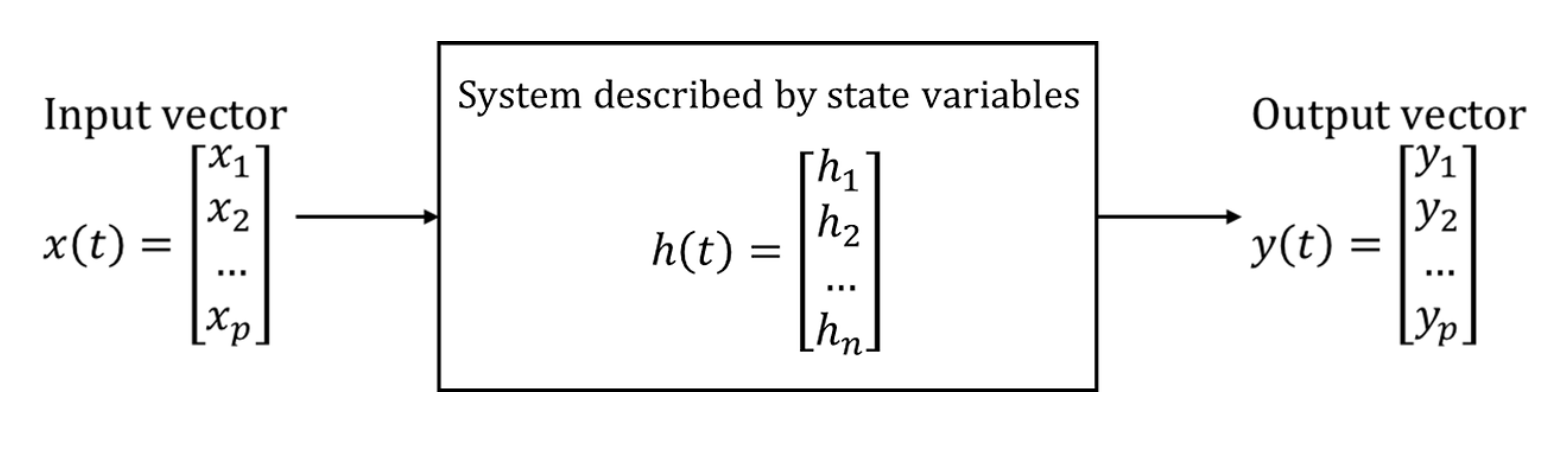
SSM의 가장 큰 특징은 RNN과 CNN의 장점을 결합함으로써 기존 recurrent model들의 단점을 극복하고 있다는 것인데요,
SSM은 크게 3가지 Representation으로 표현될 수 있습니다:
-
연속 표현 (Continuous Representation)
-
순차적 표현 (Recurrent Representation)
-
합성곱 표현 (Convolution Representation)
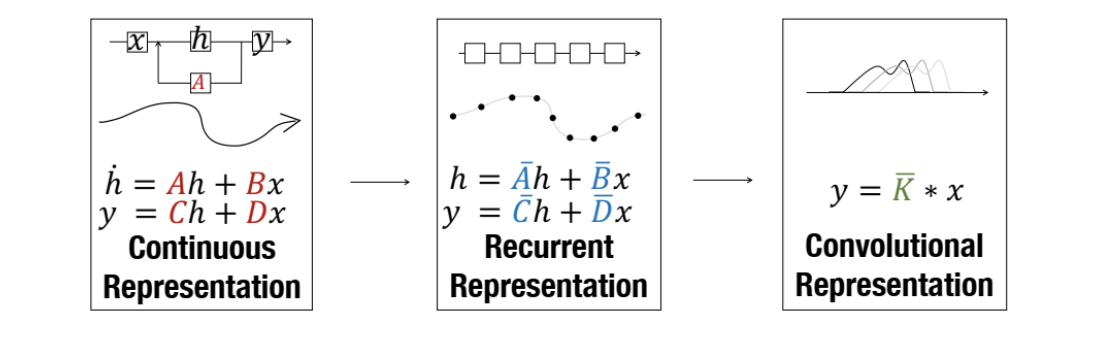
1. Continuous Representation
가장 먼저 SSM은 연속 표현(continuous Representation)을 처리할 수 있으며, 이를 통해 시퀀스 데이터의 연속성을 자연스럽게 모델링할 수 있습니다.
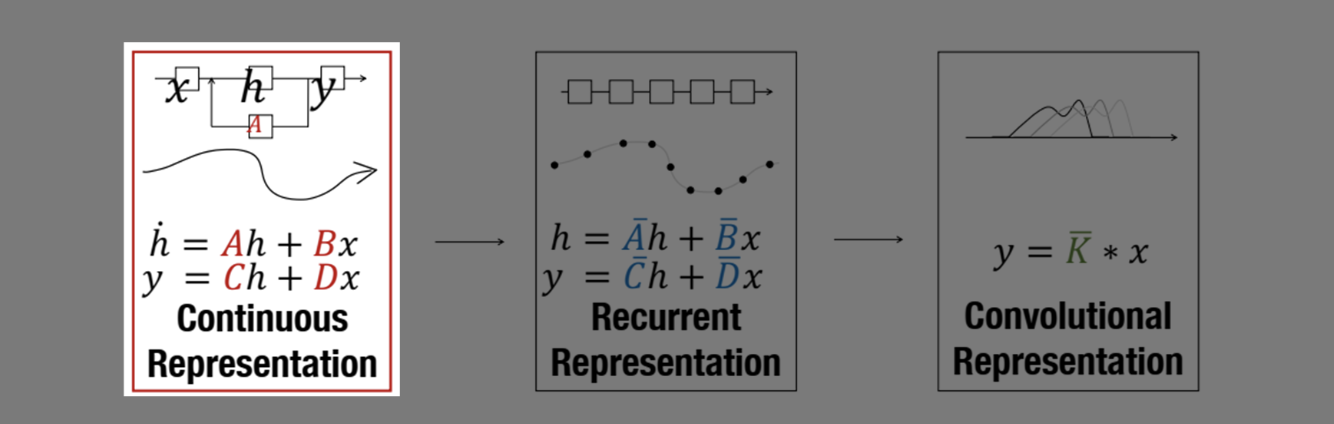
LTI(linear and time-invariant) 시스템에서는 시스템의 현재 상태를 기술하는 방정식인 **상태 방정식(State equation) **을 1차 선형미분방정식으로 표현 가능합니다.
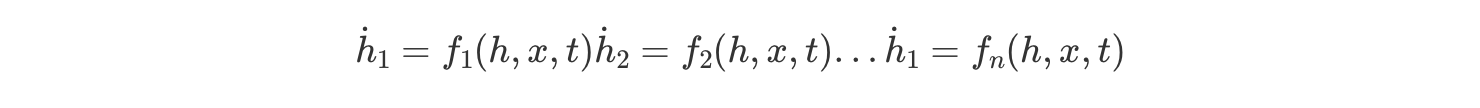
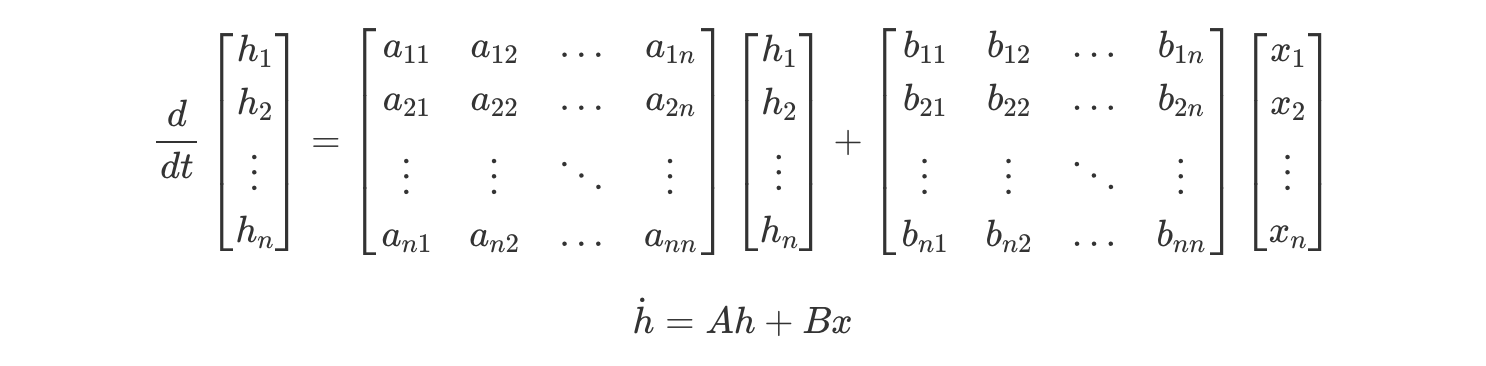
비슷한 방식으로 출력값을 표현할 수도 있습니다:
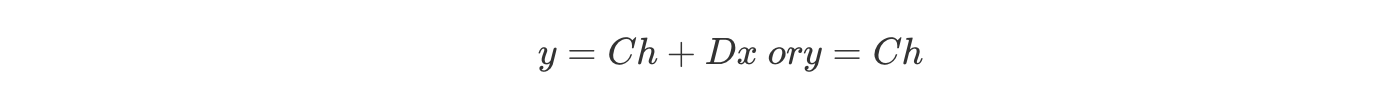
따라서, LTI system을 standard state space form으로 표현하는 모델은 다음과 같습니다:
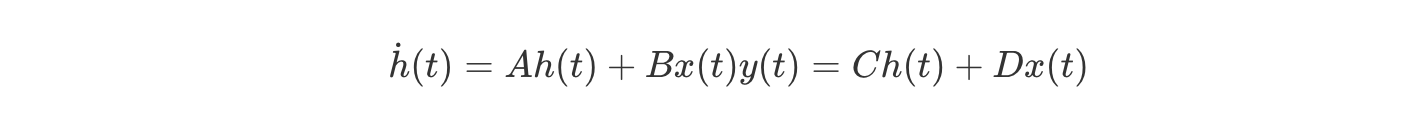
여기서 각 행렬들의 역할은 다음과 같습니다:
-
A: 기존 메모리 변환 → 메모리 업데이트
-
B: 입력 변환 → 메모리 업데이트
- 두 벡터의 합이 즉 메모리의 변화율
-
C: 기존 지식+새로운 입력을 이용해 업데이트한 새로운 메모리를 이용해 출력값 만드는 변환
이렇게 하면, A,B,C,D를 통해서, 앞서 이야기한 u(t)→y(t)를 이어주는 continuous한 flow h(t) (혹은x(t))를 모델링할 수 있습니다.
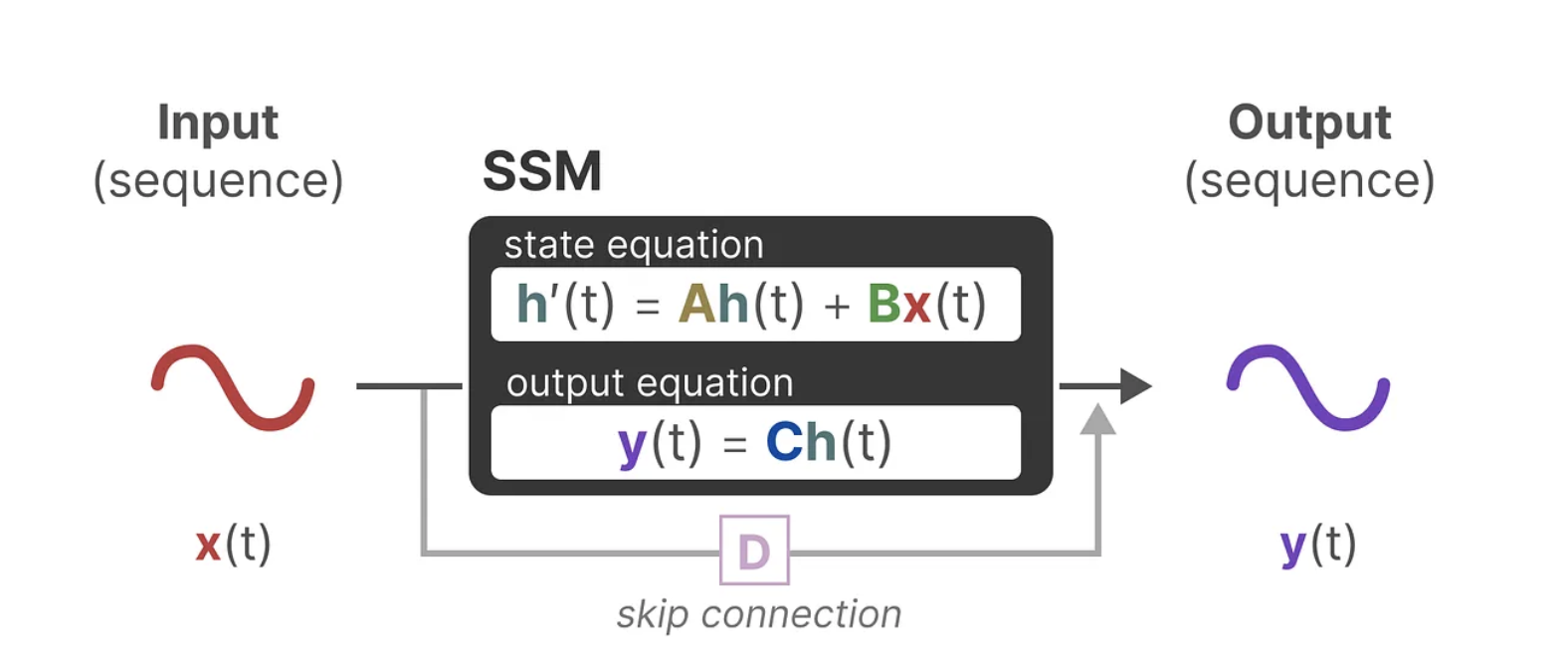
하지만, 여기서 반환되는 y는 연속된 시계열 표현(continuous-time representation)입니다. 이를 이산적인 단위를 가지는 시퀀스에서 사용하기 위해서는 discretization 작업을 수행해야 합니다.
2. Recurrent Representation
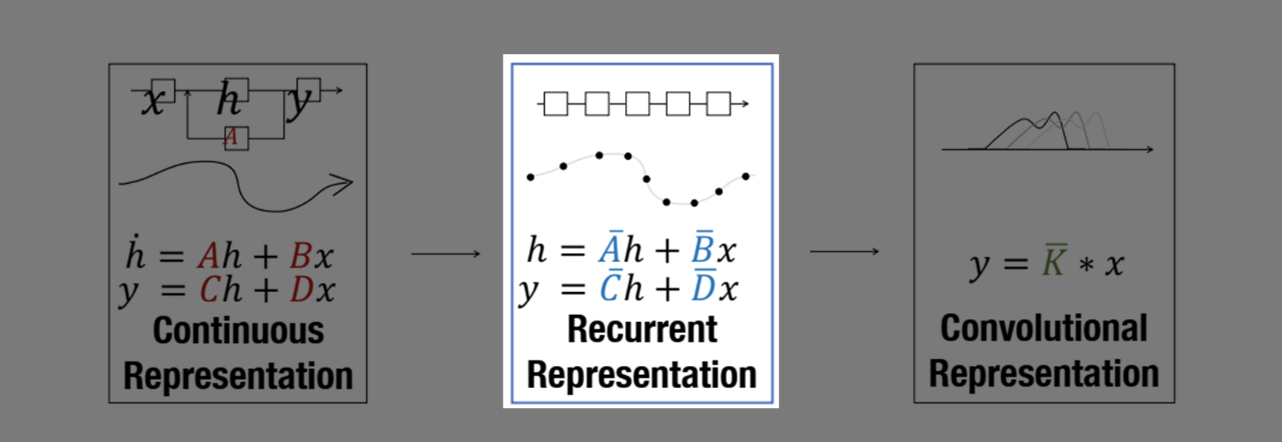
State equation은 continuous flow를 모델링하는 과정. 즉, SSM을 텍스트 차원에서 활용하기 위해서는, 연속 시스템에서 이산 시스템으로의 변환이 필요합니다.
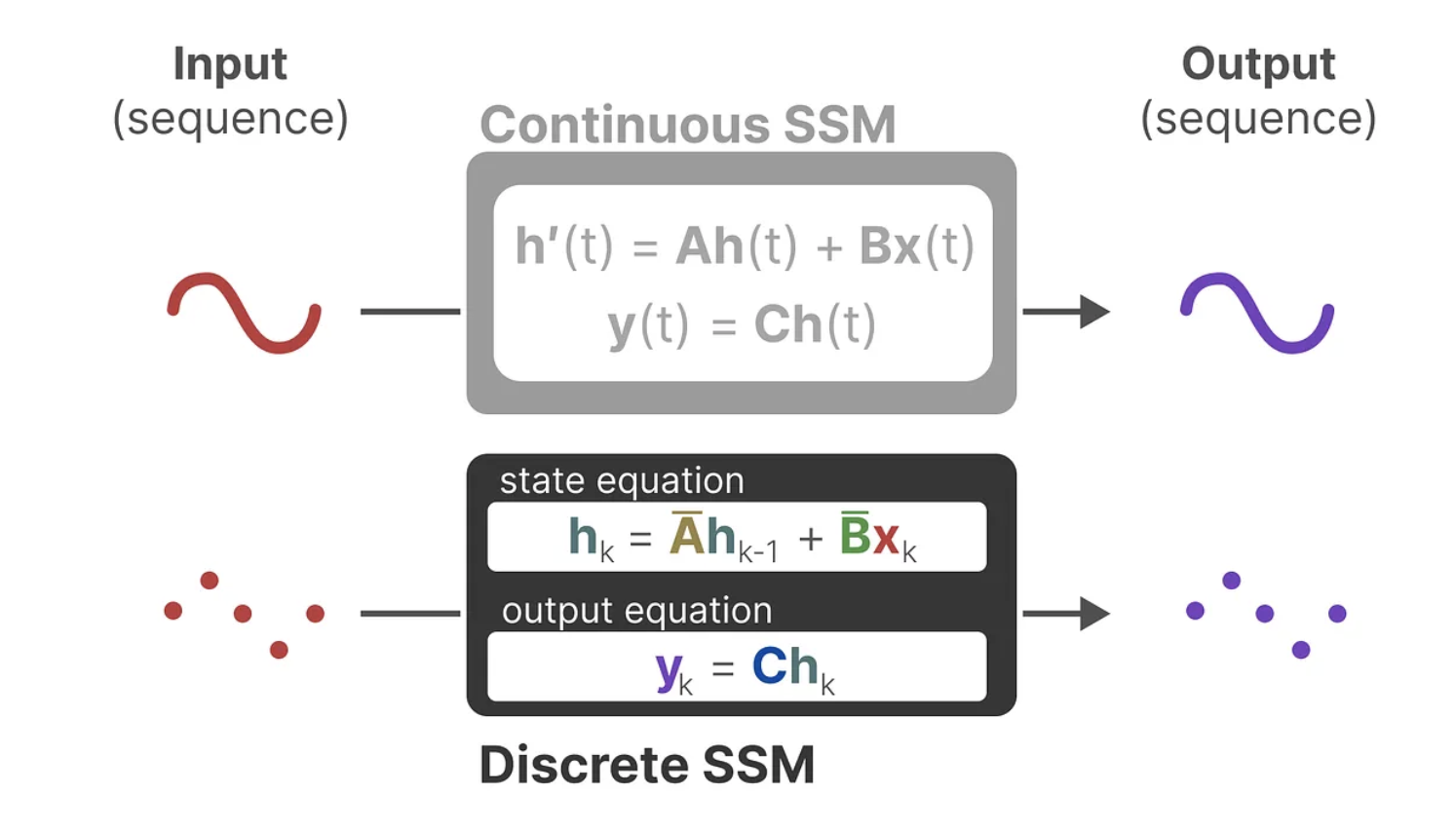
이산화를 하는데는 여러가지 방법이 있지만, 가장 간단한 방식으로는 다음과 같이, 각 시점에서 상태 공간의 변화를 나타내는 SSM 방식으로 치환할 수 있습니다:
-
h(t)=A̅⋅h(t−1)+B̅⋅x(t)
-
y(t)=C⋅h(t)
- A̅와 B̅는 SSM에서 이산화 된 버전의 매트릭스들로, 연속적인 시스템을 이산적인 형태로 변환하여 시퀀스 데이터를 처리할 수 있게 만듬. A̅와 B̅는 연속적인 SSM 모델의 도함수를 기반으로 이산적 시퀀스 처리에 맞게 변환된 것.
확인할 수 있듯, Recurrent Representation은 상태 공간 모델에서 순차적으로 상태 h(t) 를 업데이트하는 구조입니다.
즉, t번째 시간 단계에서의 상태 h(t)는 이전 상태 h(t−1)에 의존합니다.

이제 이산화한 결과를 살펴보면 다음과 같이 각각의 T=0, T=1, T=2에 대해서 이전 time t-1의 h(t-1)의 input과 현시점 x(t)의 input을 받아서 h(t)를 도출하고 이를 통해 y(t)를 재귀적으로 호출하는 것을 볼 수 있습니다.
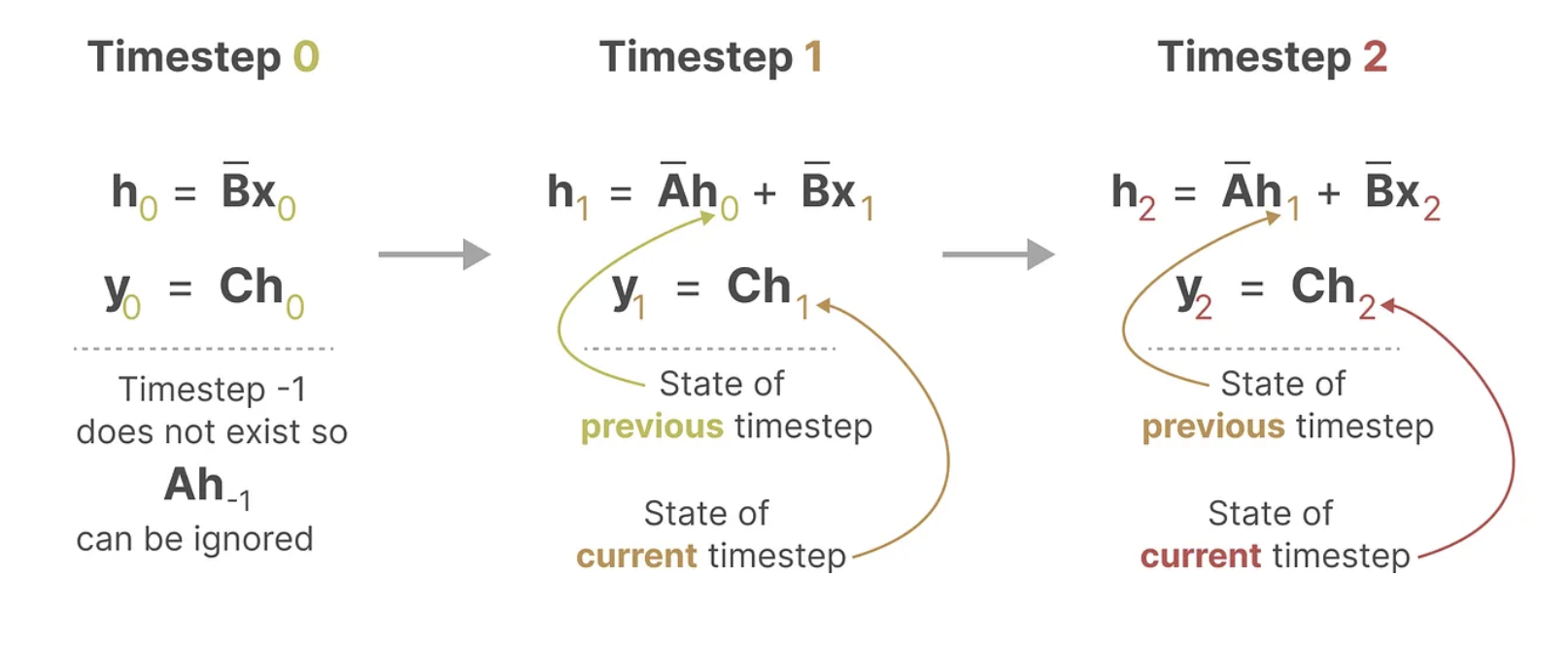
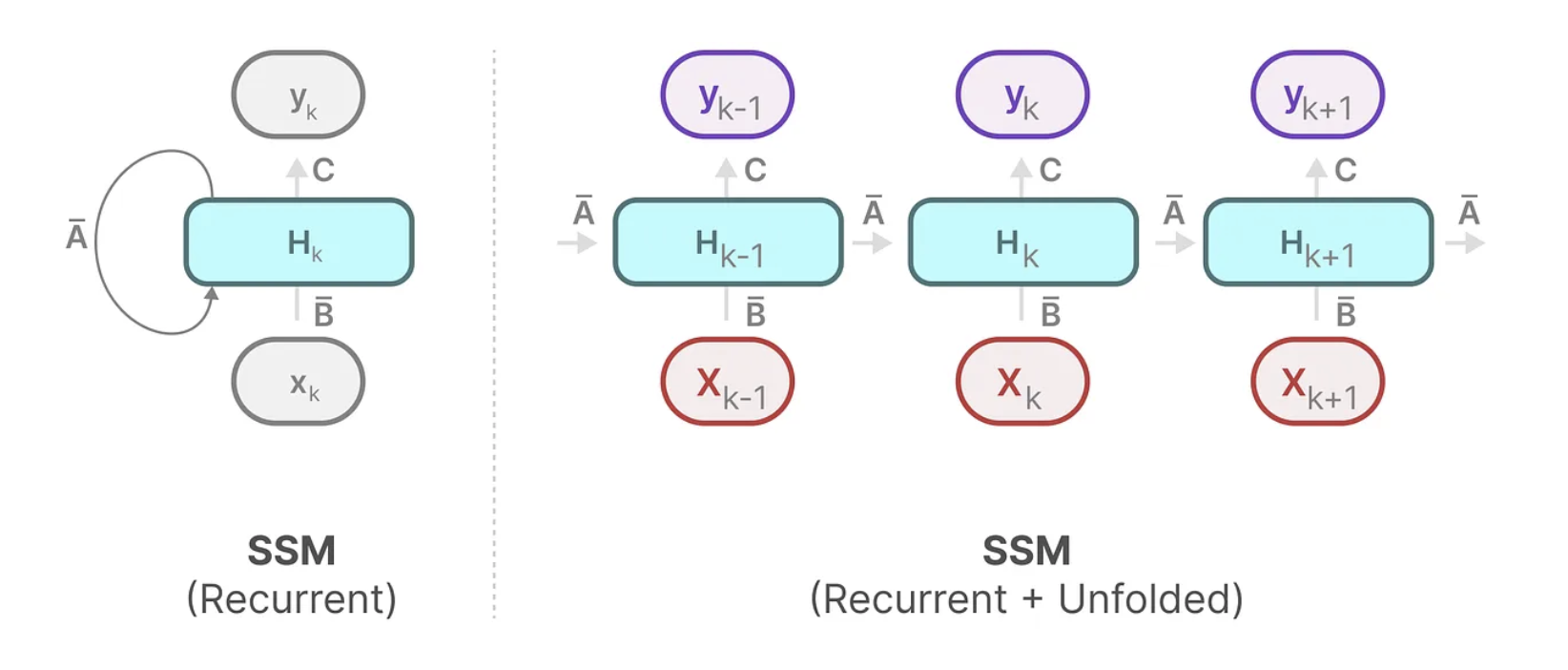
여기서 보면 RNN과 굉장히 유사한 수식이 나오지만, 둘은 본질적으로 다릅니다.
- SSM은 이산화하여 형태가 비슷해졌지만, 본질적으로 continuous하다.
-
애초에 이산화된 단위를 다루는 RNN,
-
연속적인 flow를 모델링한 뒤, 이산화를 통해 해당 단위에서도 다룰 수 있게 만든 SSM
-
SSM의 장점은 이러한 연속적인 흐름을 기반으로 시스템의 미세한 변화를 더 잘 모델링할 수 있다는 점.
- 시간 변화가 연속적인 시스템에서 데이터를 잘 반영할 수 있기 때문에 시스템의 물리적 성질을 더 정확하게 반영할 수 있음.
- SSM은 LTI, 즉 linear하면서도 time-invariant하다는 특징
-
non-linearity가 없음 (no activation) → recurrence를 convolutionize할 수 있음 → fast training 가능!
-
즉, y_t를 만들기 위해 앞선 순서를 기다릴 필요가 없이, 다 각각 kernel을 만들어서 수행을 한 다음, 합치면 됨. kernel 길이는 설정하기 나름
그런데 여기서 의문이 생길 수 있는 점은, Linear system에서 구축한 state layer가 과연 일반적인 deep RNN이 가지는 non-linearity 및 복잡도를 표현할 수 있는가에 대한 문제이다.
˙x(t)=−x(t)+u(t)의 이산화를 다르게 해석해서 Picard iteration 을 사용한다고 생각하면, 결국 deep RNN은 학습 과정에서 Picard iteration 을 거치면서 함수를 찾아간다고 생각할 수 있다. 즉, 만약 linear recurrence가 아닌 non-linear recurrence를 사용한다면 LSSL 또한 non-linearity를 학습할 수 있게 된다. 이를 통해 RNN 구조와 LSSL는 필요충분 관계에 놓여있다고 볼 수 있다. (궁금하면 참고: https://junia3.github.io/blog/lssl)
3. Convolution Representation
위에서 언급했 듯, SSM은 non-linearity가 존재하지 않기 때문에 convolutionize할 수 있습니다.
예시를 봅시다:
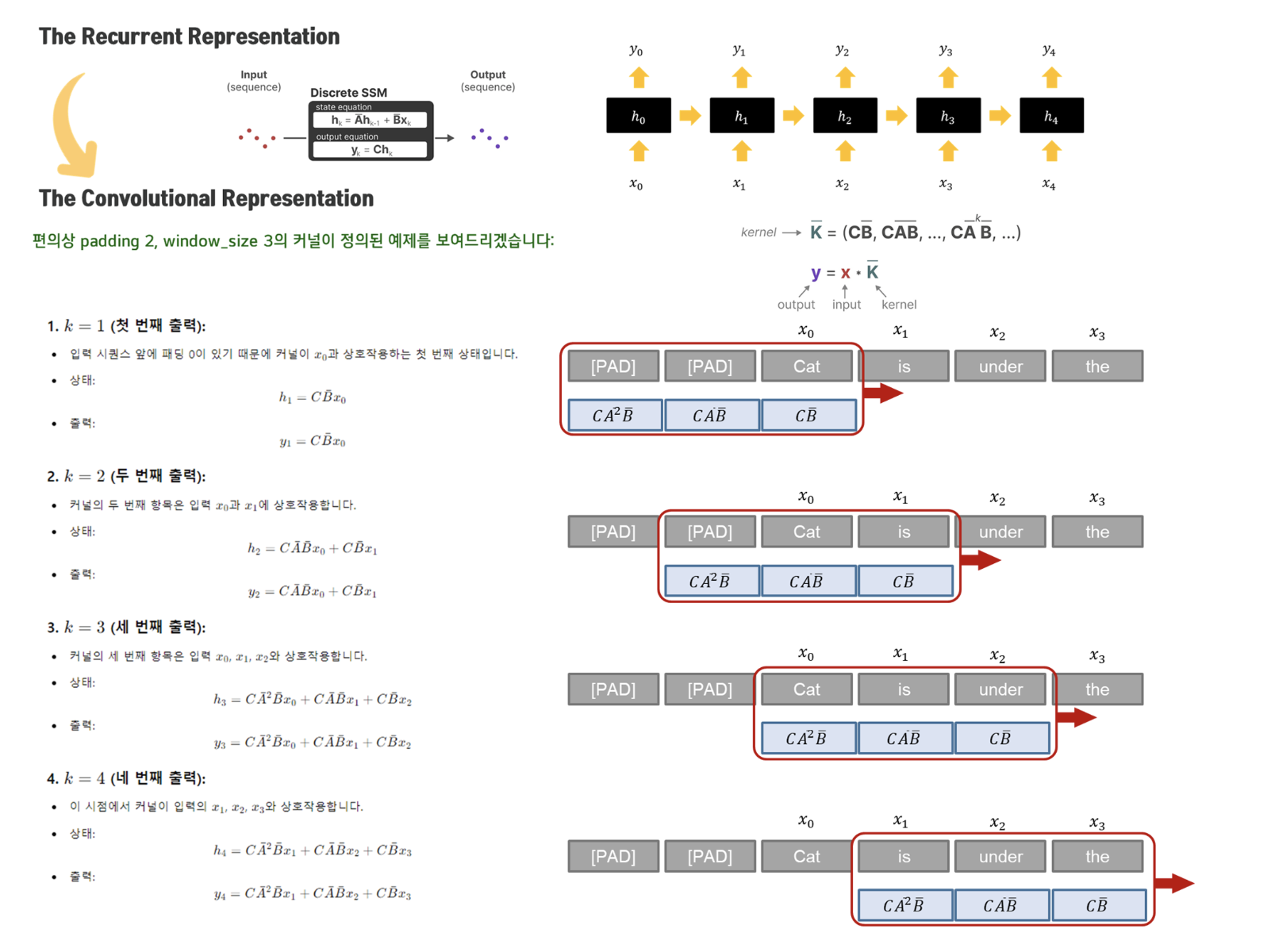
Convolution Representation 방식의 장점은 Recurrent Representation에서 각 시간 단계별로 순차적으로 상태를 업데이트하는 대신, 모든 시간 단계의 출력을 한 번에 계산할 수 있다는 점입니다.
-
병렬 처리 가능:
-
Recurrent Representation에서는 각 시간 단계별로 순차적으로 상태를 업데이트해야 하므로 계산이 직렬화되어 있음.
-
Convolution Representation에서는 커널을 이용하여 입력 시퀀스 전체에 걸쳐 동시에 출력을 계산할 수 있어, 병렬화가 가능.
-
-
더 큰 커널 적용 가능
- 더 큰 커널은 더 긴 범위의 과거 입력을 한 번에 처리할 수 있어, 더 넓은 문맥 정보를 활용할 수 있음. 이는 시퀀스 데이터에서 장기적인 종속성을 더 잘 반영하는 데 도움.
-
계산 효율성
- 합성곱 연산은 일반적으로 GPU와 같은 병렬화가 가능한 하드웨어에서 매우 빠르게 처리될 수 있음. 이는 Recurrent Representation에 비해 계산 속도에서 큰 이점을 제공.
여기까지 SSM의 개념에 대해서 알아보았습니다.
그렇다면 지금부터 Albert Gu 교수님의 연구들에서 이 SSM의 개념이 어떻게 발전되고 있는지 확인해봅시다.
Research Summary
이 논문들은 각각 시계열 데이터를 다루는 기존 모델의 한계를 극복하는 중요한 기술적 발전을 담고 있습니다.
- HiPPO: Recurrent Memory with Optimal Polynomial Projections (NeurIPS, 2020)
- 목적:
긴 시퀀스에 대한 메모리 문제를 해결하고,메모리를 효율적으로 유지하면서 입력 정보를 계속 업데이트하는 방법을 제안합니다.
- LSSL: Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers (NeurIPS, 2021)
- 목적: 이 연구는
연속 시간 모델과 선형 상태 공간 레이어(LSSL)를 결합하여,시간에 따른 연속적인 변화와 비연속적인 변화를 동시에 처리할 수 있게 만듭니다.
- S4: Efficiently Modeling Long Sequences with Structured State Spaces (ICLR, 2022)
- 목적: S4는 LSSL의 computational limit을 개선하기 위해 Convolution Representation의 효율성을 극대화하면서도,
장기적인 종속성을 더 잘 처리할 수 있게 최적화되었습니다.
- Mamba: Linear-Time Sequence Modeling with Selective State Spaces (2023)
- 목적: S4가 텍스트 데이터에 낮은 성능을 보이는 것을 selection mechanism을 통해서 개선하되, parallel scan을 통해서 속도를 유지합니다. transformer에 준하는 성능을 보입니다.
- (Mamba2)Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality (ICML, 2024)
- 목적: SSM과 어텐션 간의 이론적 연결을 확립하여 두 모델의 상호작용을 이해할 수 있는 이론적 프레임워크 제공합니다. 이를 기반으로, Transformer의 최적화 기법을 SSM에 적용해, Mamba의 성능을 크게 향상시킵니다.
1. HiPPO: Recurrent Memory with Optimal Polynomial Projections (NeurIps 2020)
[GOAL] finite한 공간에 어떻게 시간에 따라 변화하는 데이터를 압축된 형태로 유지하며, 각 시간 t에서 과거 데이터를 효율적으로 표현할 수 있는가?
-
기억해야하는 funcion f(sequence), 즉, t 시점 이전의 모든 히스토리를 제한된 메모리(hidden state) 내에 잘 압축해서 가지고 있어야 한다.
-
HiPPO는 time series input의 길이가 매우 길 때, 해당 input의 cumulative history를 압축하여 표현하는 방법을 제안한다.
HiPPO는 함수 근사를 위한 일종의 동적 시스템 방법론으로, 주어진 함수 f(t)를 시간에 따라 압축하고 저장하는 과정을 다룹니다.
이 과정은 측도(measure)에 기반한 직교 기저를 사용하여 함수를 다항식 공간으로 투영(projection)하고, 시간에 따라 변화하는 함수의 정보를 효율적으로 표현할 수 있도록 설계되었습니다.
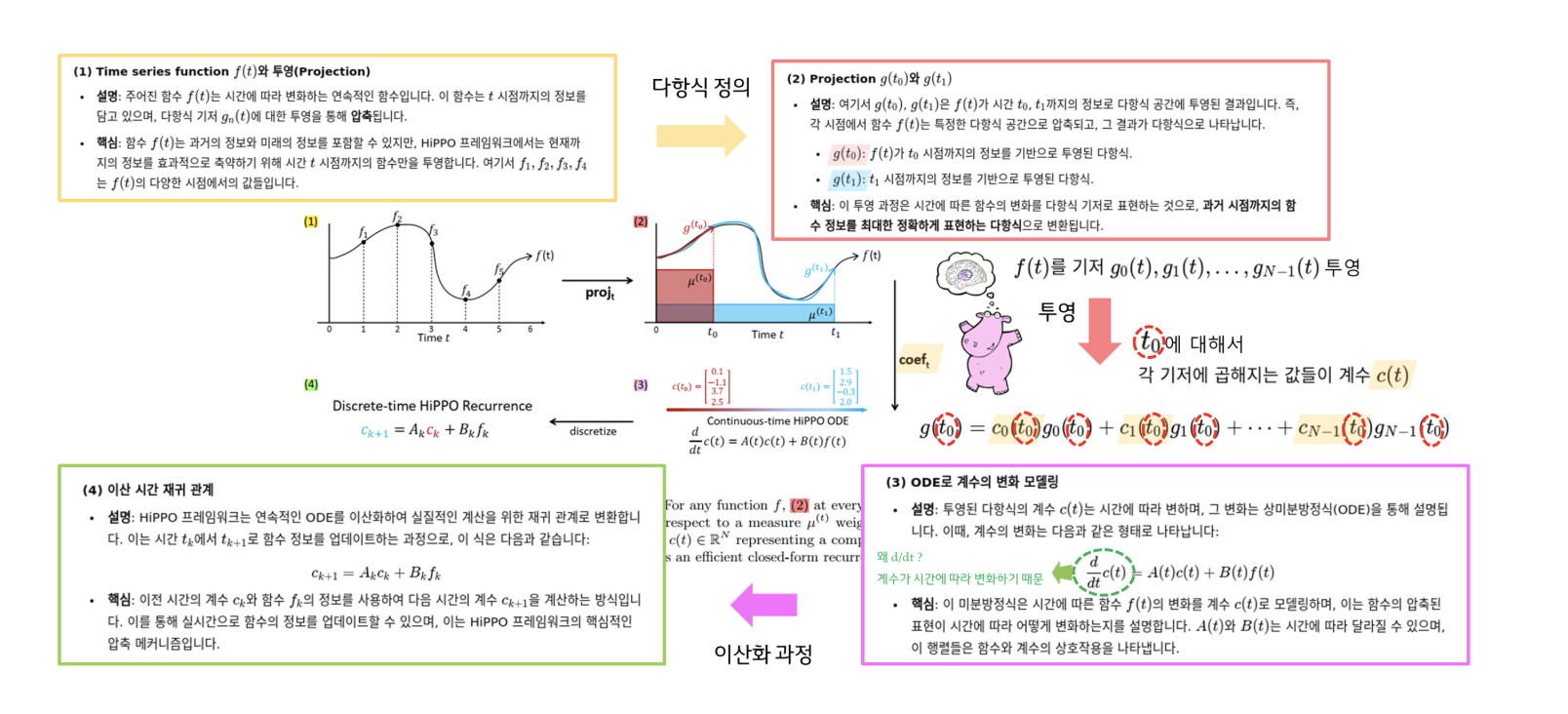
Time에 따라 변하는 (우리가 기억해야하는) 함수 f(t)가 있다고 하자.
(1) Projection 연산 : 함수 ***f*(*t*)를 다항식 공간으로 투영**
-
각 시간 t0, t1 , … T에 따라 optimal하게 projection되는 polynomial function g(t)가 존재한다고 하자
-
이때, f를 우리가 잘 다룰 수 있는 함수 g에 projection 한다.
-
투영 연산자 proj는 함수 f(t)를 일정 시간 t까지의 정보로 제한하여 다항식 공간 G에 투영합니다. 즉, 주어진 f(t)의 정보를 다항식 g(t)로 근사하여 나타냅니다.
-
g(t) : n orthogonal polynomial basis
-
이때, polynomial 기저공간(subspace)G 에 중요도에 대한 측도 (measure) μ(t)를 가중하여 투영 (projection)한다.
-
정리하자면, 투영을 통해 얻은 다항식이 시간 t 이전의 함수 정보 f≤t(x)를 최대한 정확하게 표현하는 것이 중요하기에, 주어진 측도 μ(t) 하에서 오차가 최소화되도록 다항식 g(t)로 함수를 근사하는 것이 목표!
(2) Coefficients 계산: 계수 ***c*(*t*) 구하기**
-
즉, n개의 정규직교하는 다항함수를 가지고 f를 근사하겠다
-
그럼 n개의 함수에 대한 가중치를 생각해볼 수 있음 → 이 가중치가 c(t)
-
g(t)를 R^N space vector를 가지는 coef. **c(t)로 mapping.**
-
잘 정의된 기저 공간에 대해, 얻어진 각 basis에 대한 coefficients c(t)∈\RN 는 함수 f의 history를 잘 압축할 수 있다.
-
c(t)는 즉, f를 g에 projection했을 때, 그 간격을 최소화하는 coefficient
-
-
투영된 다항식 g(t)는 다항식 기저 함수들의 선형 결합으로 표현되며, 각 기저 함수에 곱해지는 계수 c(t)는 시간에 따라 변화.
-
HiPPO는 이 계수 c(t)를 효율적으로 계산하여, 함수 f(t)의 과거 기록을 압축하는 방식으로 표현
(3) 미분 방정식 (ODE)으로 계수의 진화 모델링
-
그렇다면, 이런 좋은 coefficient를 어떻게 얻냐?
- 적절한 basis와 measure를 선택하게 되면 (A,B→ 훈련의 대상은 아님), c(t)의 업데이트 룰이 해석적으로 도출이 된다. 도함수를 통해 계산된다!
→ 이는 즉, 어떠한 시점 t에서도 히스토리를, 선정한 polynomial basis상에서 가장 최적으로 projection하는 coefficient를 찾을 수 있다!
-
투영된 함수의 계수 c(t)는 시간에 따라 진화하며, 이 변화는 상미분 방정식(ODE)으로 표현됩니다:
-
이 방정식은 계수 c(t)가 시간 t에 따라 어떻게 변화하는지를 설명합니다. A(t)와 B(t)는 각각 계수와 함수의 변화율을 나타내는 행렬.
-
중요한 점은, HiPPO가 이 ODE를 통해 함수를 시간에 따라 온라인 방식으로 압축한다는 것. 즉, 실시간으로 함수의 정보를 저장하고 진화.
-
(4) Discrete-time HiPPO Recurrence (이산 시간 재귀 관계)
-
해당 시스템을 이산화하면 online으로 추가되는 데이터에 대해 효율적인 closed-form recurrence 시스템을 구성할 수 있다.
-
우리가 다루는 공간은 이산적이므로, 이를 회귀 (recurrence)문제로 다시 정의.
-
measure을 통해서 A와 B matrix를 정의:
- projection matrix를 결정지을 measures에 대해서 기본적인 2가지 transition을 보여주고 있는데 (translated Legendre (LegT), translated Laguerre (LagT)) 현 시점에서는 중요하지 않아 생략!
-
이 과정을 통해, HiPPO는 함수의 과거 기록을 선형 결합의 형태로 압축하여 저장하고, 실시간으로 업데이트
그렇다면 얘가 왜 SSM?
→ 수식을 잘 보면: continuous한 g(t)를 구성하는 matrix는 A와 B **(HiPPO framework: A * C + B* f)
C=1, D=0으로 고정
class HiPPO(nn.Module):
"""Linear time invariant x' = Ax + Bu."""
def __init__(self, N, method='legt', dt=1.0, T=1.0, discretization='bilinear', scale=False, c=0.0):
"""
N: the order of the HiPPO projection
dt: discretization step size - should be roughly inverse to the length of the sequence
"""
super().__init__()
# (1) method를 통해서 measures 정의. (transition 함수)
self.method = method
self.N = N
self.dt = dt
self.T = T
self.c = c
# continous한 g(t)를 구성하는 A와 B matrix 정의.
A, B = transition(method, N)
A = A + np.eye(N)*c
self.A = A
self.B = B.squeeze(-1)
self.measure_fn = measure(method)
# State Space Model (SSM) 정의를 위한 C와 D를 각각 1과 0으로 설정.
C = np.ones((1, N))
D = np.zeros((1,))
# 현재 continuous function이므로, 이를 discrete하게 만들어주기 위해 signal.cont2discrete 적용.
dA, dB, _, _, _ = signal.cont2discrete((A, B, C, D), dt=dt, method=discretization)
dB = dB.squeeze(-1)
self.register_buffer('dA', torch.Tensor(dA)) # (N, N)
self.register_buffer('dB', torch.Tensor(dB)) # (N,)
self.vals = np.arange(0.0, T, dt)
self.eval_matrix = basis(self.method, self.N, self.vals, c=self.c) # (T/dt, N)
self.measure = measure(self.method)(self.vals)
def forward(self, inputs, fast=True):
# forward 함수를 통해서, coeff를 계산.
"""
inputs : (length, ...)
output : (length, ..., N) where N is the order of the HiPPO projection
"""
inputs = inputs.unsqueeze(-1)
u = inputs * self.dB # (length, ..., N)
if fast:
dA = repeat(self.dA, 'm n -> l m n', l=u.size(0))
return unroll.variable_unroll_matrix(dA, u)
c = torch.zeros(u.shape[1:]).to(inputs)
cs = []
# dA * Ck + dB * f를 통해서 Ck+1을 예측.
for f in inputs:
c = F.linear(c, self.dA) + self.dB * f
cs.append(c)
return torch.stack(cs, dim=0)
한줄 요약: HiPPO는 f(t)에 대해서 fixed probability measure를 통해 N개의 basis functions으로 구성된 polynomal g(t)를 생성하고, g(t)를 통해서 coefficients를 생성하는 f -> u 간의 mapping operator 모델
즉, SSM을 학습시키는 것은 아니고, RNN에 결합해서 사용했습니다.
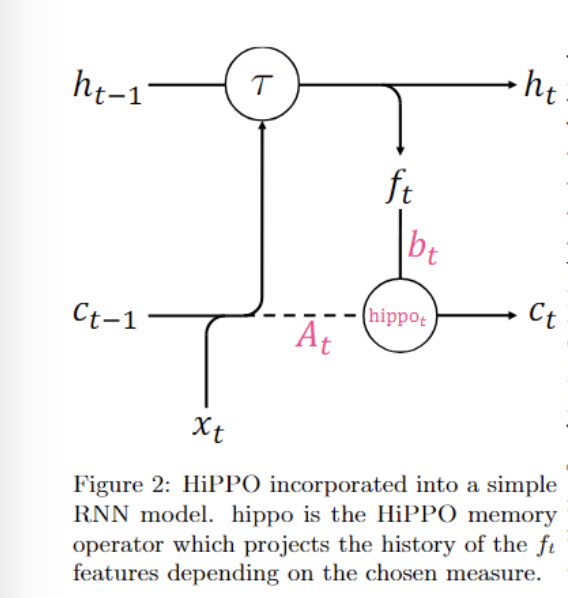
2. LSSL: Combining Recurrent, Convolutional, and Continuous-time Models with Linear State-Space Layers (NeurIPS, 2021)
[GOAL]
RNN,CNN,NeuralODE각각의 장점을 살리면서도 각 모델의 단점을 극복하는 새로운 구조인 Linear State-Space Layer(LSSL)를 제안. 주요 목표는CNN의 병렬 처리 장점,RNN의 상태 추론 능력,NeuralODE의 시간 척도(Time-scale) 적응력을 동시에 제공하는 모델을 개발하는 것입니다.
-
본격적인 SSM 아키텍쳐의 시작
-
SSM만을 stacking하여 sequential modeling
-
convoluation을 통한 fast training + recurrence를 통한 efficient inference
HiPPO 같은 경우에는 Coef.를 계산할 때 A, B, C, D가 fixed state space representation!
LSSL은 fixed하지 않는 A, B, C, D를 동시에 활용!
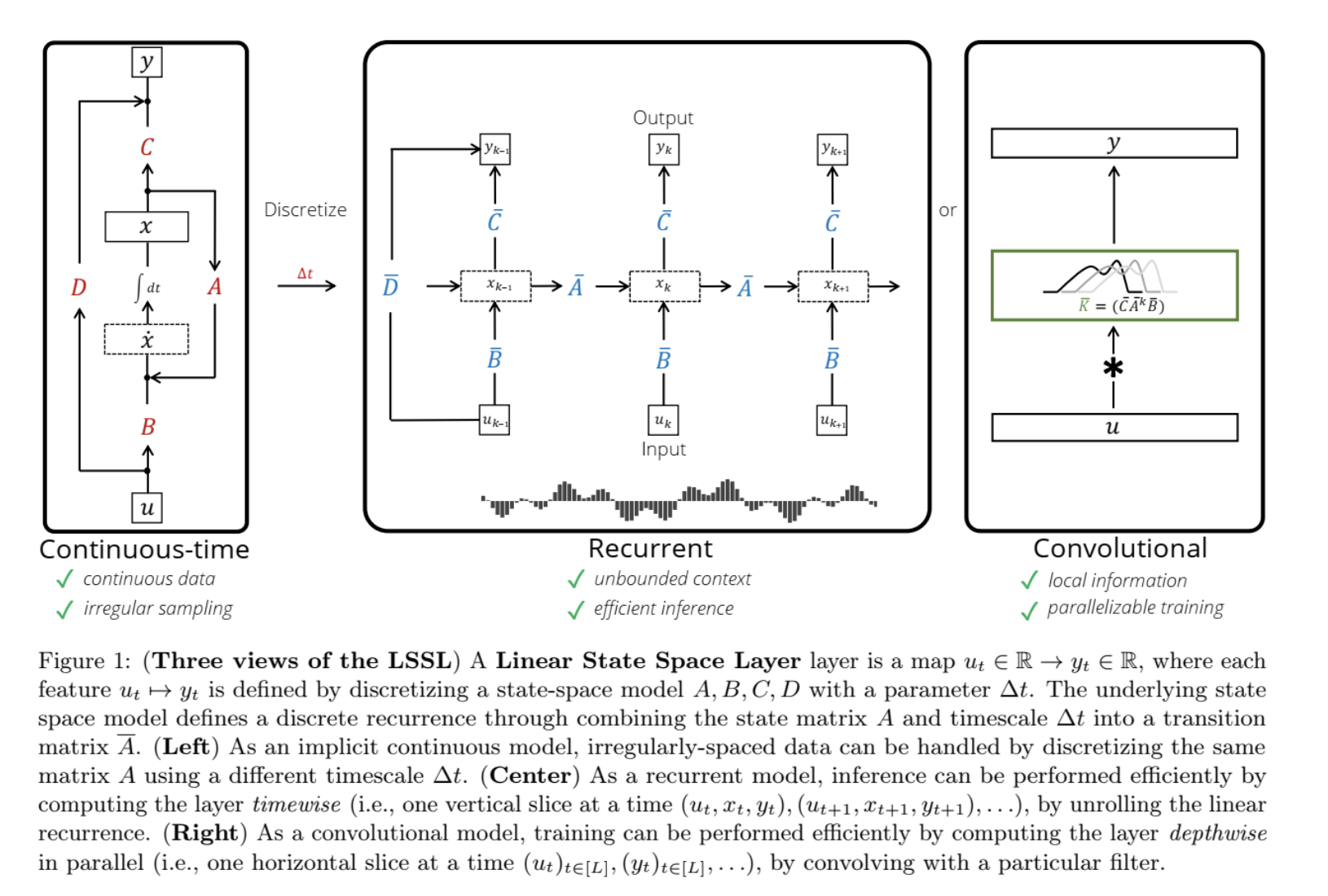
LSSL은 본격적인 SSM 아키텍쳐의 시작인만큼, 위에서 언급한 3가지 관점의 representation을 처음으로 소개합니다:
-
View 1. Continuous-time 관점:-
이 모드에서는 상태 공간 모델이 연속적 시간 t에 따라 변하며, 불규칙한 샘플링 데이터도 처리할 수 있습니다. (미분 방정식 형태)
-
식 x˙(t)=Ax(t)+Bu(t)는 상태가 시간에 따라 어떻게 변화하는지 나타내며, 출력은 y(t)=Cx(t)+Du(t)로 정의됩니다.
-
-
View 2. Recurrent 관점:-
이산화(Discretization)를 통해 RNN과 같은 형태로 사용할 수 있으며 시간 간격 Δt에 따라 상태가 변화하고, 이전 상태 정보 xk−1를 사용하여 현재 상태 xk와 출력을 계산합니다.
-
이를 통해 무한한 문맥(Unbounded Context)을 처리할 수 있으며, 효율적인 추론이 가능합니다.
-
-
View 3. Convolutional 관점:-
합성곱적 방식으로도 표현이 가능합니다. 합성곱 커널 K는 선형 시스템을 기반으로 계산되며, 이를 통해 입력 시퀀스에 대해 병렬로 처리할 수 있습니다.
-
CNN과 같이 로컬 정보(Local Information)를 사용하면서도, 병렬화된 훈련이 가능하다는 장점이 있습니다.
-
즉, LSSL은 Input u_k가 들어왔을 때,
-
Xk = u_k * B + Xk-1 * A
-
u_k에 B matrix를 곱하고 (linear)
-
이전 hidden state cell의 X_k-1에 A matrix를 곱하고 (linear)
-
-
output yk = X_k * C + uk * D
-
이렇게 총 A,B,C,D 4개의 layer parameters를 훈련하면 된다!

A, B, C, D를 각각의 linear layer라고 두고 state space model을 디자인 하게 되는데, **최종적으로 time step Δt와 A가 모델의 성능과 데이터셋을 예측하는데 중요한 역할**을 한다는 것을 알아냈습니다.
→ A matrix는 메모리의 업데이트를 담당. 잘 담는게 중요!
→ State matrix A가 학습 가능하도록 설정했을 때, HiPPO에서 제안한 state matrix A보다 성능이 더 잘 나올 수 있음을 보임.
특히, LSSL을 하나의 레이어로 사용하지 않고 여러 레이어로 쌓아서 보다 깊은 네트워크로 확장할 수 있다고 합니다:
-
기본 LSSL 구조: LSSL은 R^L→R^L seq-to-seq 매핑을 수행하며, 각각의 LSSL 레이어는 파라미터 A,B,C,D와 time step Δt로 정의됨. 입력 시퀀스는 H 차원의 피처로 처리되며, 각 피처가 독립적으로 학습. -
Layer Stacking: Deep LSSL은 여러 LSSL 레이어를 쌓아서 더 복잡한 시퀀스 데이터를 처리할 수 있음. 각 레이어는 서로 다른 상태 공간 파라미터와 시간 간격을 학습하여, 다차원적인 시간 척도에서 데이터를 처리.
그러나 실제로는, 다음과 같은 문제들이 존재합니다:
- 연산 메모리 문제 때문에 활용이 어려움
-
single input-single output을 만들어내던 A,B,C가 각각 d_model만큼 존재
-
즉, 차원마다 SSM 시스템이 개별적으로 존재 → d model개의 element들은 모두 독립적으로 다뤄짐
- vainishing gradient 문제 존재
-
A를 random initialization하면 업데이트가 잘 안된다는 문제 존재 → Hippo 방식으로 A를 initialize
- 거의 모든 deep SSM 모델들은 A를 Hippo Matirx로 초기화
3. S4: Efficiently Modeling Long Sequences with Structured State Spaces (ICLR, 2022)
LSSL 논문에서 언급했듯, SSM은 딥러닝에 적용하기에는 computational burden이 매우 커 practical하지 않습니다.
Discrete-time SSM (recurrent SSM)에서 computational cost의 주 요인은 A matrix의 반복된 곱셈 연산입니다.
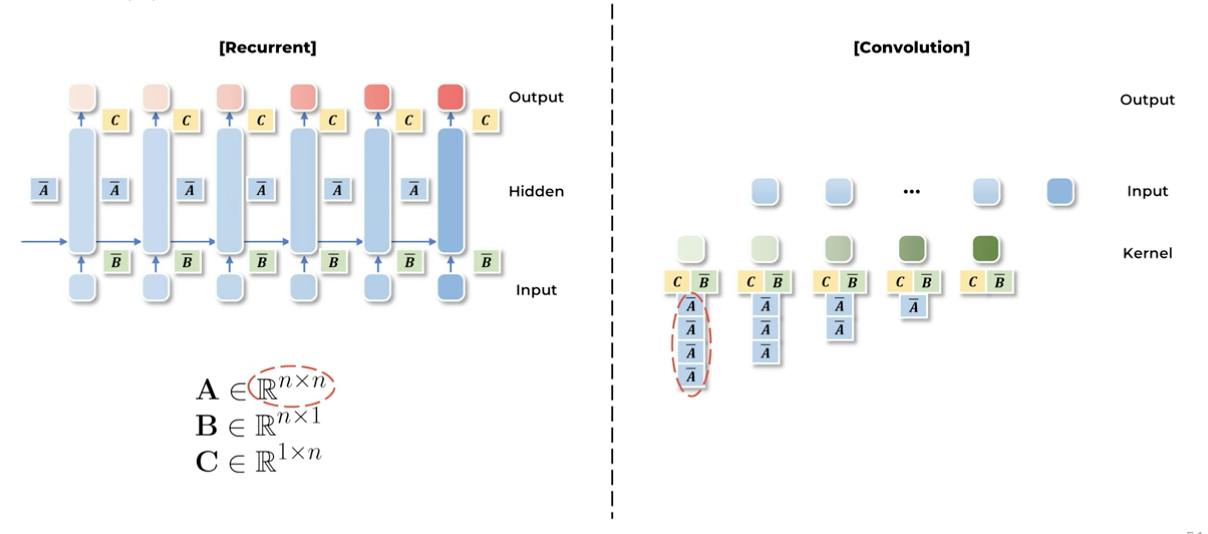
상태 공간 모델(SSM)의 중요한 문제는, 상태 공간의 크기가 커짐에 따라 연산 복잡도가 증가한다는 것입니다. 구체적으로, HiPPO 행렬 ***A***를 여러 번 곱하는 연산이 복잡도를 증가시키는 주 원인입니다.
-
그림에서 볼 수 있듯, 상태 업데이트를 위해서는 A를 여러번 곱해야함
-
A를 직접 계산하면 O(N^2L)에 달하는 연산량과 O(NL)의 메모리 공간이 필요. 이는 특히 대규모 시퀀스 모델링에서 병목이 됨.
-
심지어 deepSSM을 적용하기 위해 stacking하여 A가 d_model개 있다고 생각하면 더더욱 computation 적으로는 학습하기 어려운 모델이 되는 것
-
입력과 출력이 d_model 차원으로 확장된다면, 모든 차원을 동시에 처리하기 위해 하나의 공통된 SSM 매트릭스 **(A,B,C)를 사용하는 것을 생각해볼 수 있지만, 이는 **LTI 시스템의 요구 사항을 위배. 차원별로 독립적인 처리가 이루어지지 않으면 차원 간의 상호작용이 발생하고, 시간에 따라 결과가 달라질 수 있기 때문.
S4(Structured State Spaces)는 이를 해결하기 위해 상태 공간 모델의 수학적 강점을 유지하면서도, 이를 더 효율적으로 계산할 수 있는 방법을 제공합니다.
-
대각화 (Motivation: Diagonalization)
-
A를 직접 계산하는 메모리 및 연산 문제는 켤레(conjugation)라는 수학적 기법을 도입하여 연산을 단순화할 수 있음
-
Lemma 3.1에서 상태 공간 모델(SSM)의 행렬 A, B, C에 켤레 변환을 적용하면 동일한 모델을 얻을 수 있음을 보여줌. 켤레 변환을 할 시, 대각화나 정규형으로의 변환이 가능해짐
-
*Lemma 3.2: **HiPPO 행렬 A*가 대각화될 수 있음을 보임. 이를 통해 연산을 간소화할 수 있음
-
diagonalization을 통해서 time-complexity가 O(N^2L)에서 O(NL)까지 줄어드는 것을 확인할 수 있다!
-
Normal Plus Low-Rank Parameterization (NLPR)
-
그러나 diagonalization을 통해서 A, B, C를 conjugate하는 방법은 아쉽게도 HiPPO matrix에서 numerical issue로 계산이 안 될 수 있음 (대각 행렬이 아니여서)
-
이를 해결하기 위해, 논문에서는 정규 행렬(normal matrix)과 저랭크 행렬(low-rank matrix)의 합으로 분해하는 NPLR (Normal Plus Low-Rank) 방법론을 통해 계산의 안정성과 효율성을 높임.
-
저랭크 행렬의 항목 수가 적기 때문에 이 방법을 사용하면, A를 여러 번 곱하는 연산의 복잡도를 대폭 줄일 수 있음.
-
general하게 모든 SSM 관점에서 (HiPPO matrix도 포함) diagonalization을 통해서 A를 V^{-1}AV와 처럼 표현하기 위해 NPLR을 도입했다고 생각해볼 수 있습니다.
따라서, NPLR을 Lemma 3.1에 대입하게 된다면 SSM은 (A, B, C) ~ (Diagonal - PQ*, B, C)로 재정의 할 수 있다. 즉, S4는 총 5개의 trainable parameters(P, Q, B, C, diagonal)를 훈련하게 된다!
-
S4 Algorithms and Computational Complexity
-
S4는 Cauchy kernel을 사용하여 효율적인 계산을 가능하게 하며, 이로 인해 긴 시퀀스를 처리하는 데 필요한 연산량과 메모리 사용량을 크게 줄일 수 있음.

H3: Hungry Hungry Hippos: Towards Language Modeling with State Space Models
S4는 continuous한 task에 대해서는 잘하지만 language modeling을 못한다는 문제가 존재했습니다. H3 저자들은 S4가 어떤 task를 못하는지 분석하여 이 원인을 파헤쳐봅니다.
-
inductive head
-
정해진 special token 뒤에 어던 글자가 왔었는지 기억하고 생성하는 task
-
associative recall
-
여러 Key-value쌍을 기억해서 주어진 Key에 대한 value를 생성해내는 task
이 두 개를 못하기 때문에 S4가 언어모델링을 잘 수행하지 못한다고 주장하며, 두 개의 능력을 심어줌으로써 이를 개선할 수 있다고 주장합니다:
-
T 시점의 token 정보를 t+m 시점까지도 delay&convey하는 능력
-
지금 시점에 input된 정보를 지금 시점의 memory와 비교하는 능력
이 두 개의 능력은 input에 대해 sequence 방향으로의 Conv1D layer를 추가하는 것으로 쉽게 해결할 수 있다고 주장합니다.
(이후 내용은 크게 중요하지 않아 생략)
4. Mamba: Linear-Time Sequence Modeling with Selective State Spaces
지금까지 언급된 것처럼 SSM은 재귀적 신경망(RNN)과 합성곱 신경망(CNN)의 이점을 결합한 모델로, 시퀀스의 길이에 비례하는 선형적인 계산 복잡도를 가지고 있어 매우 효율적입니다.
하지만, 많은 고민에도 불구하고 SSM은 정보 밀도가 높은 텍스트 데이터에서는 Transformer만큼의 성능을 내지 못한다는 치명적인 단점이 존재합니다.
Mamba는 선택 메커니즘을 도입한 Selective State Space Model(선택적 상태 공간 모델)을 기반으로 하며, 긴 시퀀스를 다루면서도 Transformer 수준의 성능을 유지하면서도 계산 비용을 줄일 수 있는 모델입니다.
즉, mamba는 S4+selection (S6) 모델! S가 6개여서 mamba라고 이름 붙였다고 하네요. 요런 느낌..

물론 transformer만큼 강력하지는 않기 때문에 보편화되지 않았겠죠?! 그래도 대항마라고 엄청 화제가 된 모델인데 ICLR2024 리젝당한 것은 신기한 사실. 실험 결과가 부족하다는 평을 들었다고 하네옹
**Selective State Space Models **
(1) Motivation: Selection as a Means of Compression
H3 논문에서도 언급 되었듯, S4와 같은 LTI 시스템은 language modeling에서는 좋지 않은 성능을 보입니다. 저자들은 이를 해결하기 위해서는 두 가지 task에 대한 능력이 향상되어야 된다고 주장합니다.
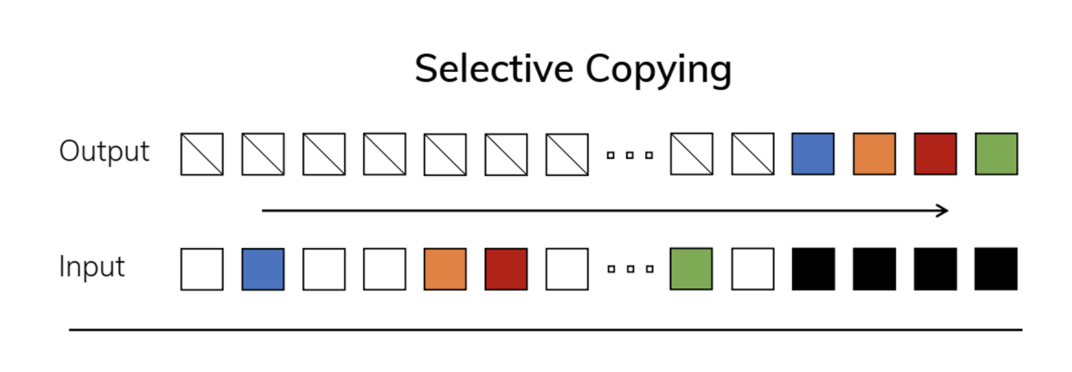
- Selective Copying Task
-
단순히 시퀀스 데이터를 기억하고, 특정 위치에서 복사하는 작업인 Copying Task는 입력과 출력 간의 간격이 일정하게 유지되기 때문에, LTI(Linear Time-Invariant) 모델로 쉽게 처리할 수 있는 단순한 작업.
-
Selective Copying Task는 Copying Task와 달리, 입력과 출력 간의 간격이 일정하지 않고 랜덤하게 변동됩니다.
-
모델은 시퀀스 내에서 중요한 정보를 선택적으로 기억하고, 나머지 불필요한 정보는 무시해야 함.
-
hidden ht에 x_t를 선택적으로 update. 특정 토큰만 update!
-
-
기존 구조로 가능한가? no!
- 왜냐면 input에 따라서 action이 달라져야한다는 것인데, 이는 LTI 시스템 상 근본적으로 불가
-
이 문제를 해결하려면 시간 가변 모델(Time-Varying Model)과 선택적 메커니즘(Selection Mechanism)이 필요.
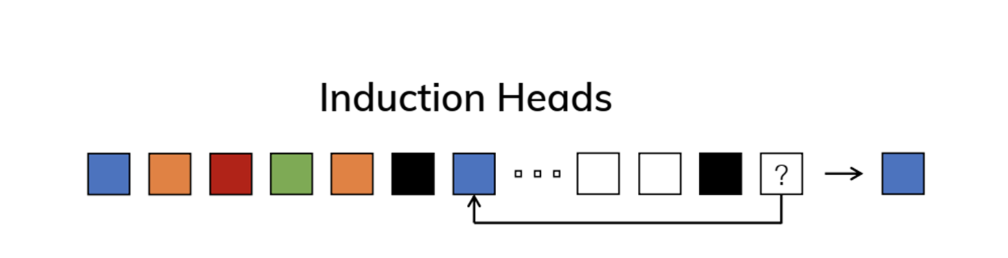
- Induction Heads Task
-
모델이 이전에 학습된 정보를 바탕으로 문맥(Context)을 이해하고, 문맥에 맞는 출력을 유추하는 task
-
선택적 메커니즘과 함께 연관 기억 메커니즘을 사용하면, 모델이 문맥을 기반으로 필요한 정보를 기억하고, 새로운 입력이 들어올 때 그 정보를 다시 사용할 수 있음
(2) Improving SSMs with Selection
저자들은 위의 두 가지 task에 대해서 SSM이 잘 작동하게 하기 위해 Selection Mechanism을 도입합니다(SSM + Selection (S6)).
Selection Mechanism은 SSM의 주요 매개변수(time step Δ,B,C) 세 가지를 입력에 따라 선택적으로 변동시킴으로써 시퀀스의 중요한 부분을 선택적으로 기억하고, 불필요한 부분은 무시하게 합니다.
당연히, 이 선택 메커니즘은 LTI를 유지하지 않기 때문에 시간에 따라 동적으로 변화하는 시퀀스를 처리할 수 있지만, 이 때문에 kernel의 형태로 병렬화를 할 수 없게 되기에 연산 속도를 위해서 추가적인 알고리즘이 필요합니다.
우선, selection mechanism을 적용한 S6를 S4와 비교하며 알아봅시다.

계산 방식: 선형 재귀 또는 합성곱 연산을 사용하여 시간 불변적 처리만 가능
S4에는 LTI 시스템이기 때문에, (D, N)의 고정된 파라미터가 모든 시퀀스에 동일하게 적용됩니다.
-
파라미터 A, B, C:
A,B,C는 모두(D, N)형태로 존재하며, 여기서 D는 입력 차원, N은 숨겨진 차원(hidden state). 고정 파라미터. -
이산화 (discretization): continuous 시스템을 이산화하여 A, B 매트릭스의 값을 변환하는 연산을 수행하는데, 이때 사용하는시간 간격
Δ는(D)크기의 파라미터. -
S4에서는 고정된 Δ가 사용됩니다. 이산화된 Δ는 각 시퀀스에 대해 각각의 매트릭스 A, B와 곱해져 ht를 업데이트합니다.

S6은 입력 및 출력의 형태는 동일. 차이는 선택 메커니즘을 적용해 입력 데이터에 따라 파라미터가 변화한다는 점!
즉, S6에서는 입력 의존적인 선택(selectivity)이 추가되어 시점에 따라 달라지는 방식으로 처리됩니다.
-
매개변수 변화:
-
*B***, *C**: S4에서는 고정된 매개변수였으나, S6에서는 sB(x), sC(x)와 같은 함수로 입력 x*에 따라 변화합니다. 즉, B,C를 직접적으로 학습시키는 것이 아닌 linear operator를 학습.
-
Δ: S4에서는 고정된 값이었으나, S6에서는 sΔ(x)를 통해 입력에 따라 변화. 이산화된 Δ는 각 시퀀스에 대해 각각의 매트릭스 A, B와 곱해져 ht를 업데이트. 이는 모델이 시점에 따라 가변적인 시간 스케일을 적용할 수 있게 함.
-
-
작동 방식:
-
매개변수 A, B, C와 시간 스케일 Δ는 입력 데이터 x에 따라 변화합니다. 이를 통해 각 시퀀스마다 다른 매핑이 일어납니다.
-
각 시점에서 재귀적 계산(recurrence)만 수행되며, 이는 시간에 따라 변화하는 time-varying 모델입니다. 특히, 각 시퀀스마다 다르게 이산화된 파라미터가 적용되기 때문에 각 토큰에 맞는 연산이 수행됩니다.
-
[정리]
-
입력 의존성
-
S4: 고정된 파라미터를 사용하여, 모든 시점에서 동일한 계산을 수행. 즉, 모든 시점에서 동일한 방식으로 입력 데이터를 처리.
-
S6: 선택 메커니즘을 통해 입력 데이터 x에 따라 매개변수들이 동적으로 변화하기에 데이터의 특성에 따라 각 시점에서 필요한 정보를 선택적으로 처리할 수 있음.
-
-
시간 불변성(Time-invariant) vs 시간 가변성(Time-varying)
-
S4: 시간 불변적인 구조로, 동일한 파라미터가 모든 시점에 적용. 이 덕분에 합성곱(convolution) 연산 가능
-
S6: 시간 가변적인 구조로, 입력에 따라 매개변수들이 변화하고, 재귀적 방식으로 계산이 이루어짐. 이를 통해 시퀀스의 각 시점에서 중요한 정보는 기억하고, 불필요한 정보는 무시하는 선택적 처리가 가능해짐.
-
-
효율성
-
S4: 시간 불변성을 유지하는 SSM은 계산의 병렬화가 가능하여, 비교적 효율적인 계산을 수행할 수 있음
-
S6: 선택 메커니즘을 추가함으로써 더 많은 계산이 필요+system matrices가 더 이상 입력에 독립적이지 않으므로 미리 global하게 적용될 수 있는 kernel을 만드는 것이 불가→ convolution을 통한 학습 병렬화가 어려워짐에 따라서 계산 효율성을 유지하기 위해서 추가적인 대응이 필요
-
(3) Efficient Implementation of Selective SSMs
어떻게 하드웨어의 메모리 계층을 최적화하여 선택적 상태 공간 모델의 성능을 극대화할 수 있는가?
추가적인 대응:
-
연산의 associativity를 이용해 parallel scan!
-
GPU의 메모리 계층을 활용한 하드웨어 최적화
-
Selective Scan & 시간 가변적 선택 처리
-
Selective SSM은 시간 가변적이기 때문에, 각 시점마다 다른 방식으로 데이터를 처리합니다. 이로 인해, 각 시점에서 중요한 정보를 선택적으로 처리하고, 재귀적 연산(recurrent operation)을 통해 이전 상태를 기반으로 다음 상태를 계산합니다.
-
Selective Scan은 시퀀스 내에서 중요한 정보를 선택적으로 처리하고, 불필요한 정보는 무시하는 과정 -
이때 각 시점에서 입력 데이터를 분석하여 중요한 정보만 선택적으로 처리하여 각 시점에서 처리되는 데이터의 양이 줄어들기 때문에, 메모리 사용과 계산 자원을 절약할 수 있습니다.
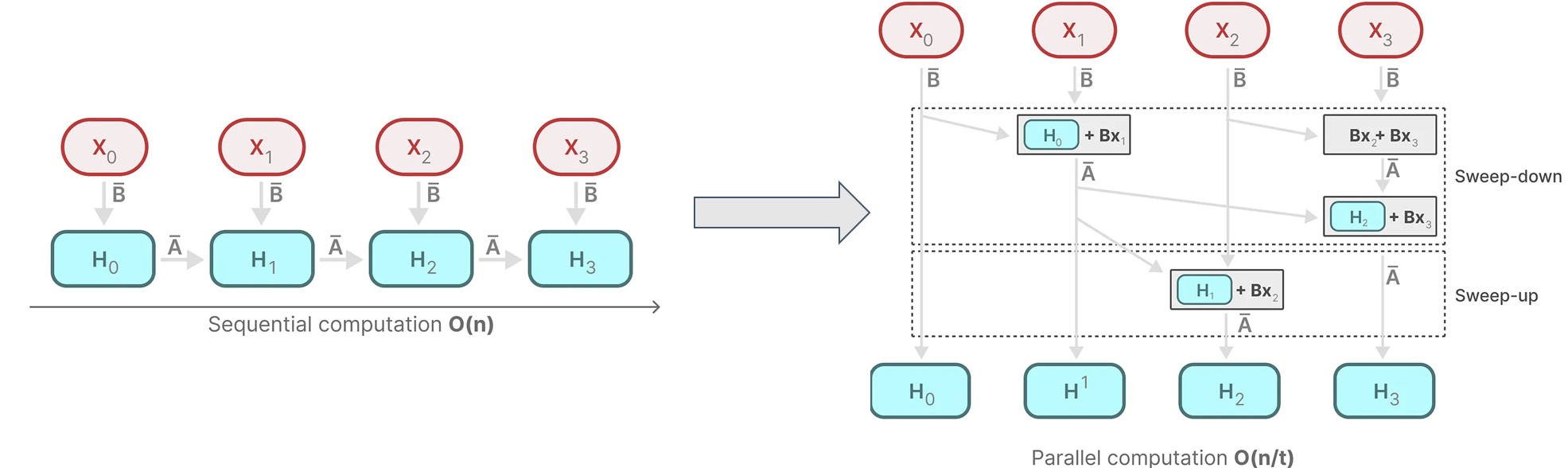
- Parallel Scan Operation
-
병렬 스캔 알고리즘(Parellel Scan Operation)은 Selective Scan 계산을 **병렬로 처리 **할 수 있도록 설계한 것
-
결합규칙(association rule) 기반 접근법을 사용하여 “먼저 계산할 수 있는 것은 계산해주자!” 라는 간단한 방법을 사용.
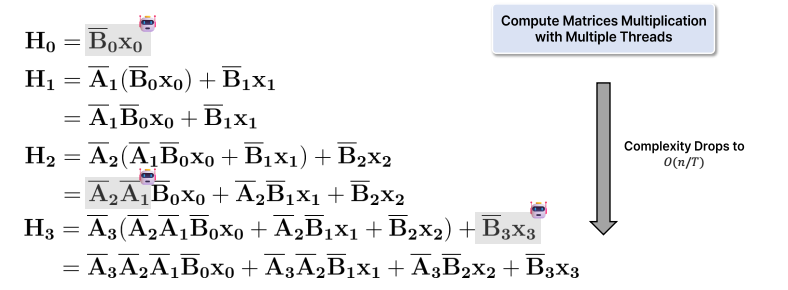
- Hardware-Aware State Expansion
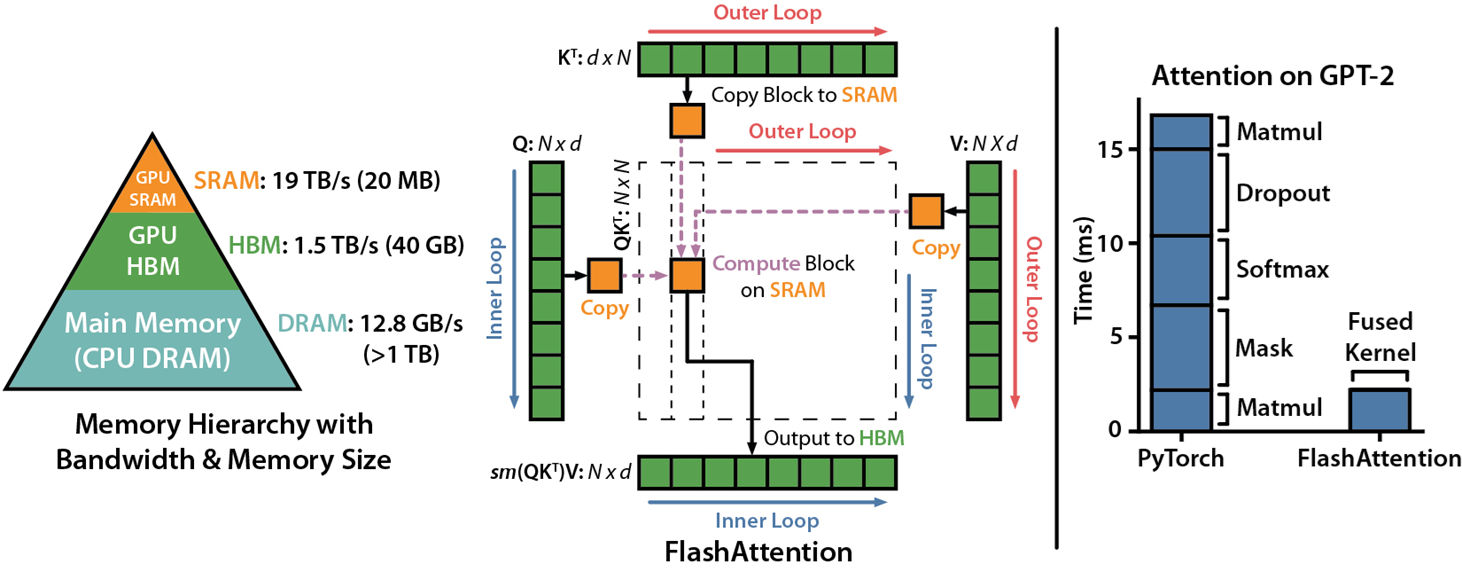
다들 아시다시피, GPU는 즉각적인 데이터 접근이 가능한 고속 메모리(SRAM)와 대용량 메모리(HBM)를 가지고 있습니다. 그리고, FlashAttention에서도 언급되었듯이, GPU의 주요 병목 현상은 SRAM과 DRAM 사이의 Copy and PASTE에서 발생합니다.
S6에서는 FlashAttention에서 나온 Kernel Fusion을 사용하여 계산의 속도를 올립니다.
즉, 입력 벡터와 가중치 매개변수를 고성능 메모리로 전송한 후 모든 계산을 한 번에 처리하고, 다시 메인 메모리로 데이터를 전송합니다.
- 이로 인해 데이터 전송 시간은 그대로 유지되면서도 16배 확장된 벡터를 사용하는 데 필요한 추가 계산 시간을 사용할 수 있게 됩니다.
→ 즉, 계산 자체의 효율성을 개선할 수 없으니 총 시간이라도 줄여보겠다!
Mamba 아키텍처
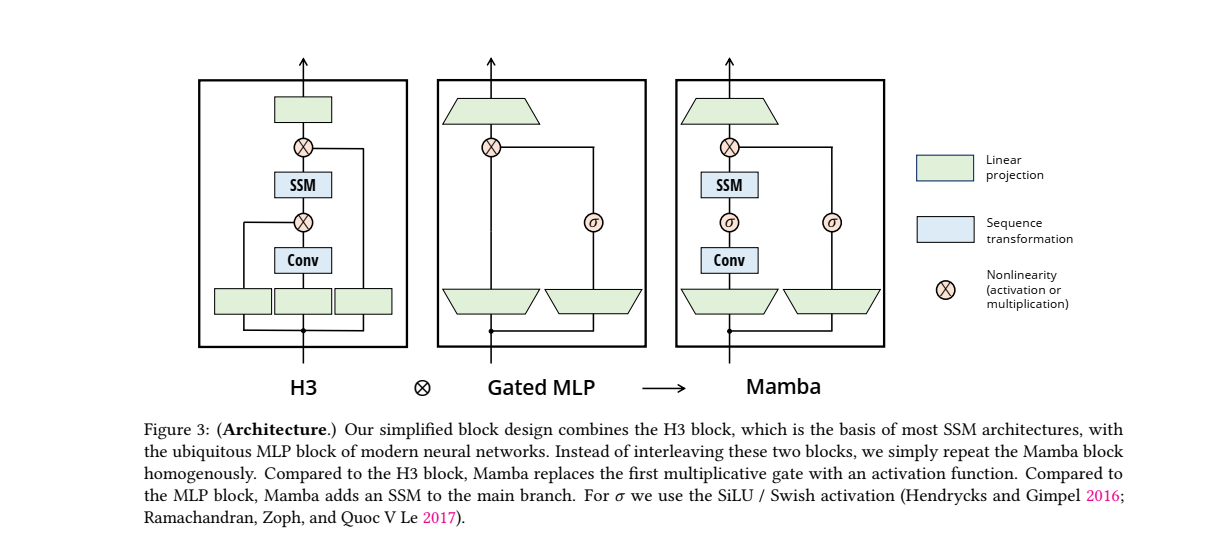
Mamba 블록은 MLP 블록과 대부분의 SSM 아키텍처의 기초가 되는 H3 블록을 조합한 것!
여러 개의 Mamba 블록을 반복적으로 쌓아 모델의 깊이를 확장할 수 있습니다.
-
구성 요소:
-
SSM: 시퀀스 데이터를 처리하는 역할.
-
Conv: 합성곱 층이 추가되어, 시퀀스 내의 국소적인 정보 처리에 기여.
-
활성화 함수(SiLU/Swish): H3와는 다르게, 곱셈 게이트 대신 활성화 함수 사용. 곱셈 게이트 대신 비선형 활성화 함수(SiLU 또는 Swish)를 사용하여 계산 복잡성을 줄이고 데이터의 표현력을 높임.
-
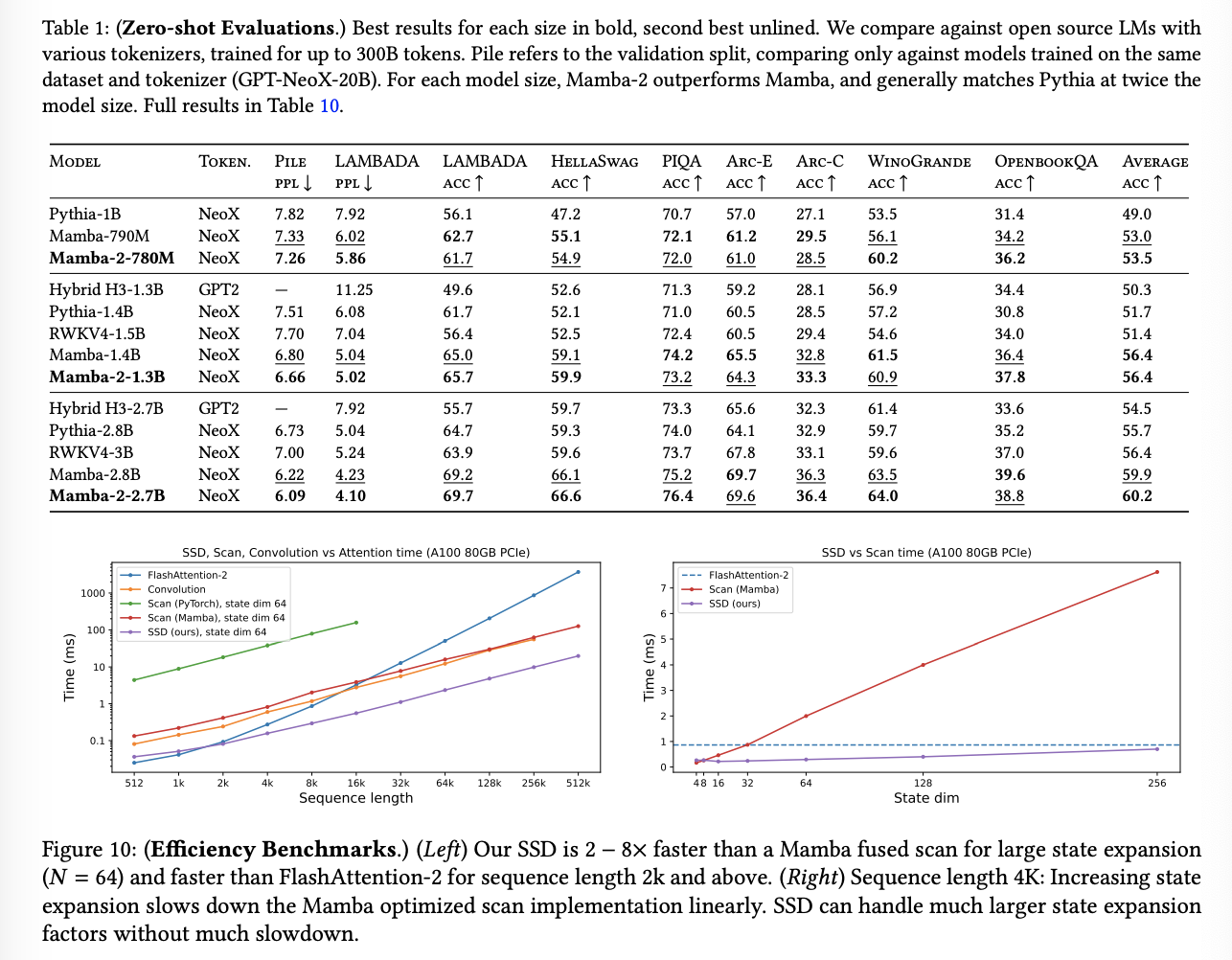
성능
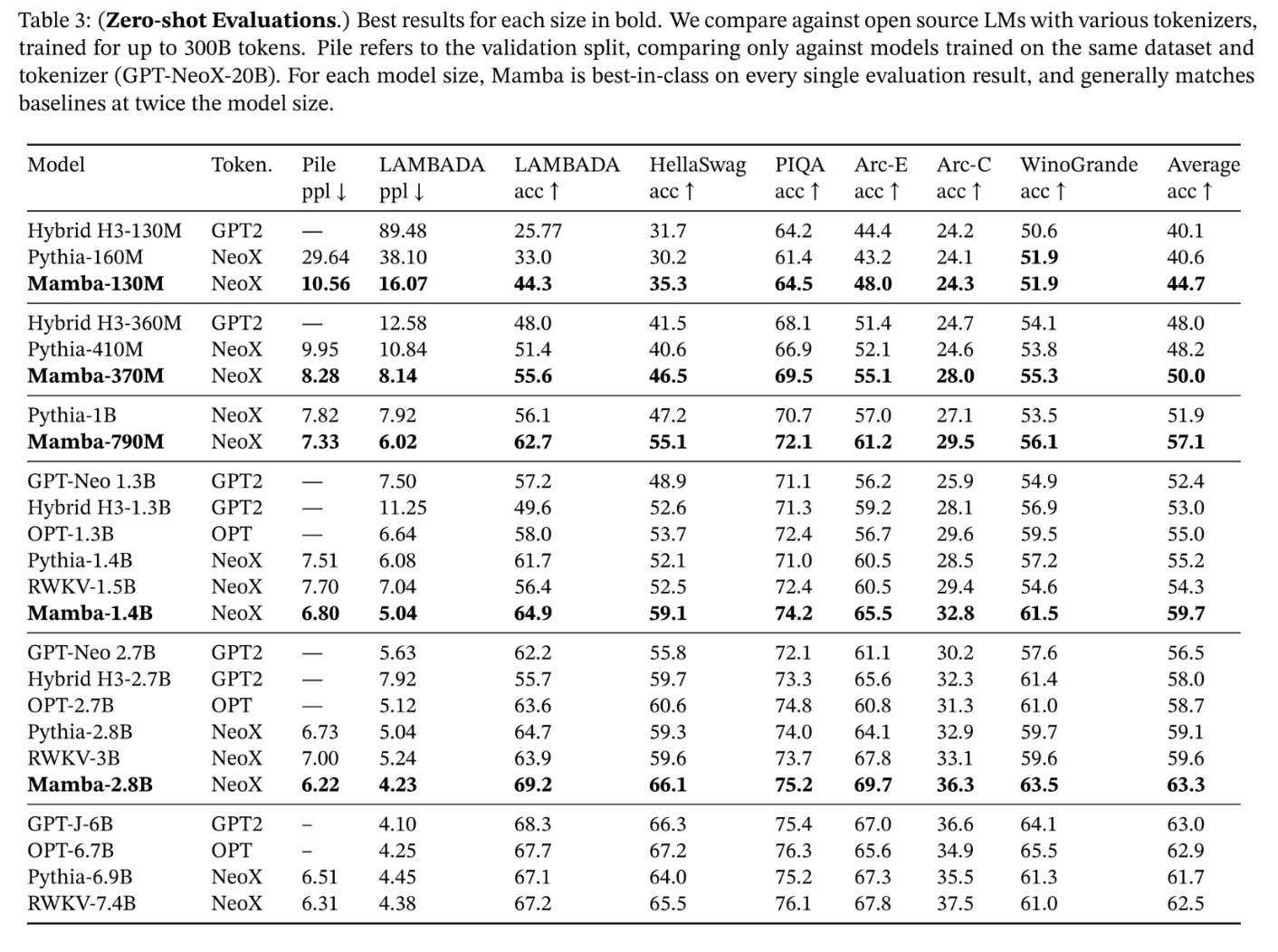
Mamba는 Transformer보다 5배 빠른 추론 속도를 보이며, 메모리 사용량도 적습니다.
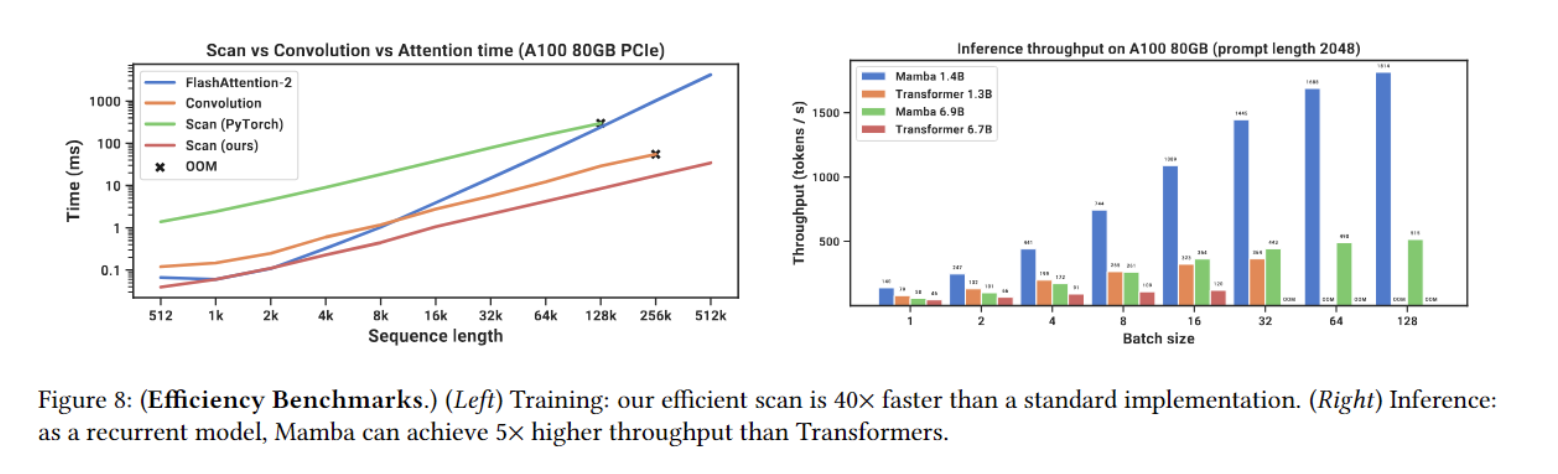
5. Mamba2 - Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality(ICML, 2024)
이 논문에서는 Structured State-Space Duality, SSD 개념을 제안하여, SSM과 Transformers의 attention 메커니즘이 서로 밀접한 관계를 가지며 특정한 수학적 변환을 통해 연결되고, 따라서, 그 동안 진행되었던 다양한 최적화 기법을 적용할 수 있음을 보입니다.
또한, SSM의 선형적 구조를 1-Semiseparable 행렬로 변환함으로써 단순 행렬 곱셈으로 치환 → 병렬화로 이어져 속도를 올릴 수 있음을 보입니다.
-
Research Questions:
-
What are the conceptual connections between state space models and attention? Can we combine them?
-
Can we speed up the training of Mamba models by recasting them as matrix multiplications?
-
1. State Space Models are Structured Matrices
SSM과 Structured Matrices
0) SSM을 수학적으로 정의하는 방식
✅ 정의 2.1: 시퀀스 변환 (Sequence Transformation)
-
SSM은 입력 시퀀스 X를 출력 시퀀스 Y로 매핑하는 함수입니다.
-
여기서 X, Y \in \mathbb{R}^{T \times P} 이며, θ는 학습 가능한 파라미터 집합.
✅ 정의 2.2: SSM 연산자 (SSM Operator)
- SSM을 연산자로 정의할 때, 특정한 행렬 연산을 수행하는 함수로 표현될 수 있음.
Y=SSM(A,B,C)(X)
✅ 정의 2.3: 행렬 변환 (Matrix Transformation)
- SSM을 하나의 행렬 연산으로 표현할 수도 있음.
Y = M_\theta X
- 이때, Mθ는 특정한 구조화된 행렬 (Structured Matrix)이며, 이를 이용해 연산을 최적화할 수 있음.
구조화된 행렬이란?
일반적인 T×T 행렬은 O(T^2)개의 매개변수를 필요로 하며, 이는 계산 비용이 큽니다.
하지만 구조화된 행렬은 특정한 구조를 가지므로, 더 적은 매개변수로 표현할 수 있으며, 연산 속도를 개선할 수 있습니다.
예시: Semiseparable Matrices (준분리 행렬)
-
Semiseparable 행렬은 특정한 계층적 구조를 가지며, 효율적인 행렬 연산을 가능하게 함.
-
SSM의 핵심 연산이 Semiseparable 행렬 연산과 동일하다는 점을 논문에서 증명.
1) State Space Models의 행렬 변환 형태
논문에서는 SSM을 하나의 행렬 변환(Matrix Transformation)으로 표현할 수 있음을 보입니다.
SSM 기본 수식
SSM은 다음과 같은 순차적(재귀적) 수식으로 정의됩니다:
ht = A h{t-1} + B x_t
y_t = C^T h_t
이를 풀어쓰면:
ht = A_t A{t-1} … A1 B_0 x_0 + A_t A{t-1} … A2 B_1 x_1 + … + A_t B{t-1} x_{t-1} + B_t x_t
이제 이를 벡터화하여 행렬 연산(Matrix Multiplication)으로 표현할 수 있습니다:
y = SSM(A, B, C) (x) = M x
여기서,
-
M은 SSM을 나타내는 특정한 구조화된 행렬입니다.
-
이 행렬은 특정한 수학적 성질을 가지며, SSM을 효율적으로 계산하는 방법을 찾는 것이 가능해집니다.
2) Semiseparable Matrices (준분리 행렬)
논문에서는 SSM이 Semiseparable 행렬과 동일한 구조를 가진다는 점을 증명합니다
✅ 정의 3.1: Semiseparable 행렬
-
Semiseparable 행렬은 특정한 부분 행렬(submatrix)이 낮은 랭크(rank)를 가지는 구조화된 행렬.
-
구체적으로, 하삼각(lower-triangular) 행렬의 모든 부분 행렬이 최대 N의 랭크를 가짐.
-
즉, 행렬 내의 각 작은 블록들이 낮은 차원의 정보만 유지하면서도 원래 행렬의 주요 특성을 보존하는 특수한 구조를 가짐.
-
이러한 행렬 구조를 이용하면 연산량을 크게 줄일 수 있음.
2.1 The Sequentially Semiseparable (SSS) Representation
✅ 정의 3.2: Sequentially Semiseparable (SSS) 표현
-
하삼각 행렬 M이 SSM과 같은 연산을 수행할 수 있도록 다음과 같이 정의할 수 있음:
- A lower triangular matrix 𝑀 ∈ R (T,T) has a N-sequentially semiseparable (SSS) representation if it can be written in the form M{ji} = C_j^T A_j A{j-1} … A_{i+1} B_i
-
SSM의 행렬 연산을 특정한 Semiseparable 행렬 구조로 표현 가능함
𝑀 = SSS(𝐴{0:T}, 𝐵{0:T},𝐶_{0:T}).

- 즉, SSM의 수식을 Semiseparable 행렬의 행렬 곱셈으로 변환할 수 있음.
✅ 정의 3.3: An N-SSS matrix 𝑀 with representation (4) is N-semiseparable.
(생략)
✅ 정의 3.4: Every N-semiseparable matrix has a N-SSS representation
(생략)
2.2 1-Semiseparable Matrices: the Scalar SSM Recurrence Semiseparable Matrices: the Scalar SSM Recurrence
1-SS
-
1-Semiseparable (1-SS) 행렬은 특정한 하삼각 행렬의 랭크가 1로 제한되는 특수한 경우입니다.
-
즉, SSM의 상태 크기(state size) N=1인 경우를 의미합니다.
-
M{ji}=a_ja{j−1}⋯a_{i+1}
-
이것을 행렬 연산 형태로 표현하면 다음과 같이 나타낼 수 있습니다.
- M=1SS(a_0:T)
-
1-SS 행렬은 다음과 같은 특정한 행렬 구조를 가집니다.

- 이 행렬은 각 타임스텝에서 이전 값을 누적 곱셈(cumulative product)하는 형태를 가짐.
1-SS 행렬을 이용한 행렬 연산은 기본적인 스칼라 SSM 재귀식(Scalar SSM Recurrence)과 동일한 형태를 가집니다
풀어쓰면:
이것이 결국 1-SS 행렬의 행렬 곱셈과 동일한 구조를 가짐을 알 수 있습니다.
즉, 1-SS 행렬의 행렬 곱셈은 결국 단순한 스칼라 재귀(Scalar Recurrence)를 반복 수행하는 것과 동일함을 보일 수 있습니다.
3) State Space Models are Semiseparable Matrices
**✅ 정의 3.5: **
SSM의 변환 연산 **y=SSM(A,B,C)(x)은 Semiseparable 행렬 M과의 행렬 곱셈 **y=Mx** 와 동일하다**
즉, 모든 SSM은 Semiseparable 행렬 변환으로 나타낼 수 있으며, 두 개념이 동등함을 의미.
이를 통해 다음과 같은 사실이 도출됩니다.
- SSM 연산을 Semiseparable 행렬 연산으로 최적화 가능
- 행렬 곱셈 최적화 기법을 적용하여 연산 속도를 크게 향상시킬 수 있음.
- Transformer의 Attention과 유사한 수학적 표현 가능
- Attention 연산도 행렬 변환으로 표현되므로, SSM을 Transformer 구조와 비교하고 최적화하는 것이 가능.
2. Structured Masked Attention: Generalizing Linear Attention with Structured Matrices
Linear Attention과 Structured Matrices
이 섹션에서는 Transformer의 Self-Attention을 분석하고, 이를 일반화하여 **Structured Masked Attention (SMA) **개념을 도입합니다.
특히, 기존의 Linear Attention이 수행하는 연산을 더 일반적인 구조화된 행렬 연산(Structured Matrices)을 이용해 확장하고 최적화하는 방법을 제안합니다.
Attention
Y=softmax(QK^T)⋅V
Autoregressive 모델에서, 과거의 정보만 사용하기 위해 **Causal Mask **(L)을 적용합니다.
Y=(L∘QK^T)V
여기서 L은 하삼각(lower-triangular) 행렬로, 미래 정보가 사용되지 않도록 만듭니다.
Linear Attention
softmax attention의 quadratic한 계산 복잡도를 개선하기 위한 하나의 대안: linear attention
기존 어텐션에서 소프트맥스(Softmax)를 제거하고 행렬 곱셈 순서를 변경하면 연산량을 줄일 수 있음.
Y=Q⋅cumsum(K^T⋅V)
선형 어텐션은 소프트맥스 함수의 계산을 제거하여, 시퀀스 길이에 따라 선형적인 계산 복잡도를 가질 수 있음
Structured Masked Attention (SMA)
논문에서는 기존의 선형 어텐션을 더 발전시켜, 구조화된 마스크드 어텐션(Structured Masked Attention, SMA)이라는 새로운 개념을 도입.
SMA는 기존의 선형 어텐션의 장점을 유지하면서도, 구조화된 행렬의 성질을 사용해 더 효율적인 방식으로 어텐션을 수행
-
기존 Linear Attention은 단순히 Causal Mask L을 사용.
-
하지만, 더 일반적인 구조화된 행렬 L을 사용할 경우, 더 강력한 모델링이 가능.
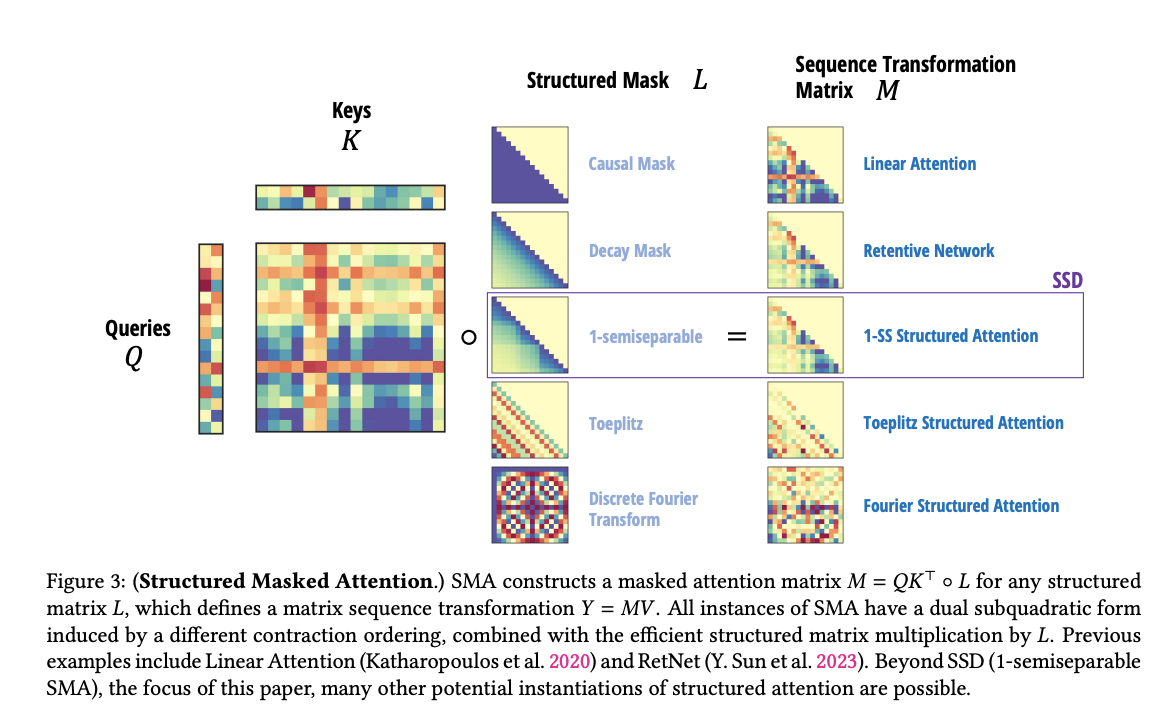
즉,L을 단순히 Causal Mask로 고정하는 것이 아니라, *입력에 따라 동적으로 변할 수 있는 구조화된 행렬(Structured Matrix)**로 확장할 수 있습니다.
3. State Space Duality
해당 섹션에서는 SSM과 SMA(attention)가 어떻게 duality 관계를 통해 서로 연결되는지를 설명하며, 두 개념이 시퀀스 모델링에서 어떤 방식으로 상호 보완적인 역할을 할 수 있는지 설명합니다.** **
-
SSM은 준분리 행렬(Semiseparable Matrix)로 표현 가능
-
SSM의 기본 행렬 변환: M{ji} = C_j^T A{j:i} B_i
-
만약 Aj가 단순한 스칼라라면, 이를 다음과 같이 변형할 수 있음: M = L \circ (CB^T)
-
이는 masked kernel attention의 수식과 동일함.
-
즉, SSM을 단순한 이차 시간 복잡도로 계산하면, 결과적으로 마스킹된 어텐션과 동일한 연산이 수행됨.
-
→ SSM과 어텐션 기반 모델이 이론적으로 동일한 방식으로 동작한다!
→ 어텐션 기법은 본질적으로 상태 공간 모델의 한 형태임.
→ 따라서, SSM의 선형 시간 복잡도 \mathcal{O}(T)를 활용해 효율적인 어텐션 모델을 설계할 수 있음
.
4. The Mamba-2 Architecture
Mamba-2는 SSM(Structured State Space Model)과 Attention의 연결을 바탕으로 **보다 효율적인 학습과 추론을 가능하게 하는 모델입니다. **
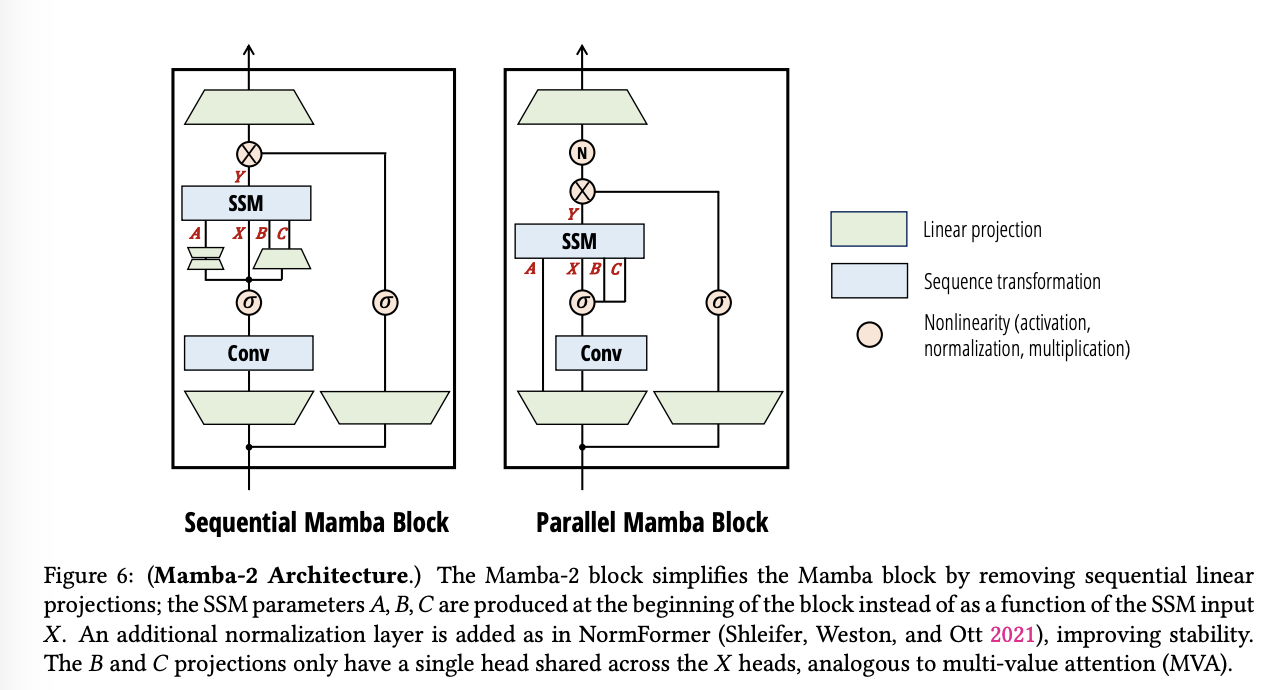
1) Block Design
Mamba-2의 블록 설계는 기존 Mamba 블록을 단순화하면서도 성능을 향상시키는 방향으로 변경되었습니다.
- ** Parallel Parameter Projections**
-
기존 Mamba-1에서는 A,B,C 행렬이 입력 X에 따라 생성되었으며, 순차적인 연산(Sequential Computation)이 필요했습니다.
-
Mamba-2에서는 A,B,C,X를 블록의 시작 부분에서 동시에 병렬 생성하도록 변경하여 연산 효율성과 병렬 처리 성능을 증가시켰습니다.
-
즉, SSM을 순차적인 재귀 연산으로 구현하는 대신, 1-SS 행렬을 통해 병렬 행렬 곱셈으로 변환
-
이는 Transformer의 Q,K,V 연산이 병렬로 수행되는 것과 유사한 개념.
-
- Extra Normalization
-
대규모 모델에서 발생하는 학습 불안정성을 해결하기 위해 추가적인 정규화 계층을 도입.
-
Mamba-2에서는 LayerNorm, GroupNorm, RMSNorm 등의 정규화 기법을 활용하여 학습 안정성을 개선했습니다.
-
이는 NormFormer (Shleifer et al., 2021)에서 사용된 기법과 유사하며, SSM 구조에서도 효과적으로 적용됨.
2) Multihead Patterns for Sequence Transformations
-
SSM은 시간에 따른 상태를 업데이트하면서 시퀀스를 변환하는 방식.
-
이를 멀티헤드 구조로 확장하면 여러 개의 독립적인 변환을 동시에 수행할 수 있어 모델의 표현력을 향상할 수 있습니다.
- Transformer에서 Multi-Head Attention (MHA)가 Q,K,V 행렬을 여러 개의 “헤드”로 분리하여 각각 독립적인 어텐션을 수행하는 것과 유사.
(Multihead 패턴 정의)
-
멀티헤드 시퀀스 변환은 H개의 독립적인 헤드를 가지며, 전체 모델 차원 D=d_model을 유지합니다.
-
각 헤드는 SSM 파라미터 A,B,C를 독립적으로 가질 수도 있고 공유할 수도 있음.
-
Transformer와 마찬가지로, H가 커질수록 모델 차원이 증가하지만, 개별 헤드의 차원 N과 P는 일정하게 유지됩니다.
-
일반적으로 N과 P를 64 또는 128로 설정하며, 모델 차원 D가 증가할 때 헤드 개수 H를 늘립니다.

- ** Multihead SSM (MHS) → Multihead Attention (MHA)**
-
가장 일반적인 멀티헤드 구조로, 각 헤드가 독립적으로 SSM을 수행합니다.
-
모든 파라미터 A,B,C가 독립적이며, 여러 개의 시퀀스 변환을 병렬로 수행할 수 있습니다.
-
일반적인 Transformer의 Multi-Head Attention (MHA) 방식과 동일한 구조.
- ** Multi-contract SSM (MCS) → Multi-query Attention (MQA)**
-
MQA는 inference 속도를 높이기 위한 최적화 기법.
- Key-Value(K,V)를 공유하여 캐싱 효율을 높이고, 연산량을 줄임.
-
Mamba-2에서는 이를 SSM의 Multi-Contract 구조로 변환하여 적용.
- B (V에 해당)와 X를 공유하고, C는 각 헤드마다 독립적.
- Multi-expand SSM (MES) → Multi-key Attention (MKA)
-
MKA는 각 헤드가 별도의 Key를 가지며, Value는 공유하는 방식.
-
Mamba-2에서는 SSM에서 C와 X를 공유하고, B는 독립적으로 유지.
-
이렇게 하면 다양한 Key를 학습하면서도, Value 공간은 공통적으로 활용 가능.
- Multi-input SSM (MIS) → Multi-value Attention (MVA)
-
MQA가 Query마다 Key-Value를 공유하는 방식이라면, MVA는 Key-Value마다 Query를 공유하는 방식.
-
Mamba-2에서는 MIS 방식으로 구현:
- B와 C를 공유하지만, X는 각 헤드에서 독립적으로 처리.
실험 결과, MVA 방식이 Mamba 모델에서 가장 효과적인 패턴으로 나타남.
5. Systems Optimization for SSMs
Mamba-2는 병렬 처리에 적합하도록 설계되었으며, 특히 텐서 병렬화와 시퀀스 병렬화(Sequence Parallelism)를 모두 지원합니다. 이는 매우 긴 시퀀스 작업에서 각 시퀀스를 여러 디바이스에 분산시켜 병렬 처리할 수 있게 하며, 각 GPU 간의 재귀 상태(recurrent state)를 효율적으로 전송할 수 있습니다.
또한, Mamba-2는 Transformer와 달리 시퀀스 길이에 따라 패딩(padding)을 사용할 필요가 없습니다. 대신, 각 시퀀스의 길이에 맞춘 효율적인 연산을 수행할 수 있기 때문에, 변동 길이 시퀀스를 처리할 때 더욱 높은 효율성을 보입니다.
(자세한 내용 생략)
6. Result