Titans: Learning to Memorize at Test Time
논문 정보
- Date: 2025-02-04
- Reviewer: 준원 장
1. Introduction
- Transformer
⇒ (1) key-value associations을 저장 (2) query를 통해 retrieve하는 방법을 학습
⇒ current context window에 직접적인 dependencies가 형성될 수 밖에 없음
- Overcome the scalability issue of Transformers
⇒ linear transformer: softmax대신 kernel trick으로 attention 계산
⇒ data가 matrix-valued states로 mapping/compressed이 되기 때문에 very long context에서 효용X
-
Limitation of recurrent neural network
-
단기 기억, 장기 기억, 메타 기억, 현재 맥락에 대한 attention을 모두 적절하게 구현한 architecture의 부재
-
구성 요소가 독립적으로 작동할 수 있는 상호 연결된 시스템의 부재
-
(LSTM, GRU가 어느정도는 하지만) 여전히 데이터를 통해 추상화된 과거 역사를 암기하는 능력이 결여
-
-
Memory Perspective
⇒ 논문에서는 Memory 관점에서 기존의 Model을 독자에게 이해시키고자 함
- memory: input에 의해서 발생하는 neural update
-
RNN
-
𝑓 (M{𝑡 −1}, 𝑥𝑡 )
-
𝑔(M𝑡, 𝑥𝑡 )
→ t번째 입력에 의해서 ‘vector-valued memory module’ M이 업데이트 되고, retreiving 되는 것의 반복
- Transformer
→ RNN과 달리 past key, value를 계속 appending함으로써 메모리 업데이트
→ matrix-valued memory Module
-
위의 논의들을 바탕으로 논문에서는 5개 RQ를 던짐
-
좋은 메모리 구조란 무엇일까?
-
적절한 메모리 업데이트 메커니즘이란 무엇일까?
-
좋은 메모리 검색 프로세스란 무엇일까?
-
(기억이 단일과정이 아니며 단일 기능도 수행하지 않고 각각 다른 신경 구조로 서로 다른 기능을 수행하며 독립적으로 작동한다는 점을 고려할 때) 서로 다른 상호 연결된 메모리 모듈을 통합하는 효율적인 아키텍처는 무엇일까?
-
(데이터를 linear manner로 벡터나 행렬에 저장한다는 가정은 oversimplification일 수도 있다) long-term memory를 효과적으로 저장/기억하려면 deep memory module이 필요한가?
-
⇒ 위의 물음에 대한 해답을 제시하면서 test time에 memorize가 가능한 architecture 제공
2. Preliminaries
Notations
-
Input: x ∈ ℝ^{(N×d_m)}
-
Neural Network Module: \mathcal{M}
-
Attention Mask: M
-
Segment
-
i번째 세그먼트: S^{(i)}
-
i번째 세그먼트의 j번째 토큰, 벡터, hidden state: S_j^{(i)}
-
-
Neural Network
-
forward pass with weight adjustment: \mathcal{N}(x)
-
forward pass without weight adjustment: \mathcal{N}^{*}(x)
-
forward pass in k-th layer: \mathcal{N}^{(k)}
-
Backgrounds
-
Transformers
-
yi = \sum{j=1}^i \frac{\exp(Qi^T K_j/\sqrt{d_m}) V_j}{\sum{l=1}^i \exp(Q_i^T K_l/\sqrt{d_m})}
-
𝑁 × 𝑑 operation이 필요함 → 긴 메모리를 처리하기 위해서는 larger memory consumption and lower-throughput
-
-
Efficient Attentions (linear attentions)
-
kernel function: \phi(x,y) = \phi(x)\phi(y)
-
attention: yi = \sum{j=1}^i \frac{\phi(Qi^T K_j)}{\sum{l=1}^i \phi(Qi^T K_l)} V_j = \sum{j=1}^i \frac{\phi(Qi)^T \phi(K_j)}{\sum{l=1}^i \phi(Qi)^T \phi(K_l)} V_j = \frac{\phi(Q_i)^T \sum{j=1}^i \phi(Kj)V_j}{\phi(Q_i)^T \sum{l=1}^i \phi(K_l)}
-
kernel 이 identity function이면 다음과 같이 recurrent format을 갖는 transformer로 전개
-
Mt = M{t-1} + K_t^T V_t
y_t = Q_t M_t
-
RNN
-
hidden state = memory units
-
recurrent process를 memory 관점에서 read/write로 해석할 수 있음
-
read(input → hidden) : y_t = g(\mathcal{M}_t, x_t) \quad \text{Read Operation}
-
write(hidden → output): \mathcal{M}t = f(\mathcal{M}{t-1}, x_t) \quad \text{Write Operation}
-
-
⇒ 이 관점에서 보면 Equation은 matrix-valued memory에 key와 value를 계속해서 write하는 과정이라 볼 수 있음
결국 sequence가 길어짐에 따라 모델이 forwarding 하면서 풀어야 하는 문제는 2개로 좁혀짐 (memory module을 잘 추가해야 하는건 여기에선 당연한 문제)
-
forget mechanism을 잘 추가해 memory 적재를 줄이느냐? (xLSTM, Mamaba2)
-
write operation를 improving시키냐? (뭐 논문 설명을 보면 잘 지우면서 write시키냐, 병렬처리학습이 가능하냐로 설명함)
3. Learning to Memorize at Test Time
논문이 제안하고자 하는것은 ‘inference time’때 long-term memory를 잘 활용하는 meta memory model → neural network (e.g., LM)이 sequence를 처리할 때 이를 적절히 ‘저장할 함수’를 파라미터로써 학습시키는 것
3.1 Long-term Memory
→ memorization이 가능한 learning function, 데이터가 들어오면 해당 데이터를 모듈이 어떻게 저장하는지에 대한 방법을 학습
-
Learning Process and Surprise Metric.
- Online learning을 차용한 후 너무나 직관적인 방법을 활용해 current sequence input x_t이 그동안의 Memory Module이 저장해온 data의 pattern과 다르면 Memory Module을 update하는 식으로 학습
→ \nabla \ell(\mathcal{M}_{t-1}; x_t)을 surprise 로 정의하는데 사실상 past sequence랑 많이 다르면 Memory Module을 많이 업데이트 하겠다.라는 전형적인 DL 업데이트
→ gradient descent with momentum의 형식과 똑같이 surprise S_t를 정함
-
\eta{t}와 \theta{t}가 모두 function of input x_t
-
data-dependent manner로 memory module을 update하는 방법을 학습시켜야 하기 때문에
(e.g., 모든 토큰이 관련성이 있고 동일한 컨텍스트에 있을 경우, recent past tokens 대비 input xt가 \eta{t} \rightarrow 1로 해야 올바르게 학습이 됨)
- Objective.
→ past data를 key와 value의 pair로 저장하는 이전 model들의 관점을 따라 아래의 loss로 memory module을 학습
-
input x_t를 사영시킨 이후 memory module이 key ↔ value의 관계를 학습시키는 방식
-
이 학습 파이프라인 관점에서 W_K, W_V는 hyperparameter
-
Forgetting Mechanism.
→ GRU, LSTM같이 forgetting 부분 도입. 해당 weight decay/forgetting 부분도 input x_t에 의해서 학습되도록 설계
-
Memory Architecture.
-
vector-valued나 matrix-valued를 활용해 memory module을 설계할 경우 → \mathcal{M}_t =w_t
- 이 경우 온라인 선형 회귀 목표를 푸는게 되고, 최적의 값은 데이터의 종속성이 선형이라는 가정을 해야함
-
따라서 논문에서 편의를 위해 편의상 표기를 ‘\mathcal{M}_t =w_t’로 하지만 expressive power를 위해 2 layer MLP를 썼다고 함
-
-
Retrieving a Memory.
- 위에서 설계한건 memory module이기에 information을 retrieve해서 current sequence해 concat해 processing을 해야 비로소 쓸모가 완성이 됨
3.2 How to Parallelize the Long-term Memory Training
→ long-term memory module 학습시에 긴 sequence를 parallel하게 학습할 수 있다.를 수식적으로 보여준 부분
-
\mathcal{M}_0에서 학습시작
-
t’: 0
-
t: b
-
\betai = \prod{j=1}^i(1-\alpha_j)
→각 청크(rank)에 관련된 행렬을 저장함으로 분산학습 가능
→ 각 chunk에 대한 u_t를 구해놓고 recurrent하게 surprise value값 구하기 가능
3.3 Persistent Memory
→ 학습 가능하지만 input-independent한 파라미터 세트를 사용하여 task-related memory로 활용하고자 함
(여기서부터 2016-2019 모델링 연구 느낌 너무 강함;;;)
-
prefix/prompt tuning처럼 sequence앞에 task-specific learnable (inference에서는 fix인) parameter를 도입
-
그럼 저자들은 이 module을 왜 도입했냐?
-
memorization of the task knowledge (prefix/prompt tuning랑 똑같음)
-
이 parameter도 결국 attention의 대상이 되는데, input-independent attention weights이 필요해서
-
attention map을 살펴보면 initial bias가 있는데 input-independent parameter가 attention distribution redistributing해줄 것으로 기대 (근데 보통 special token에 skewed걸리지 않나?)
-
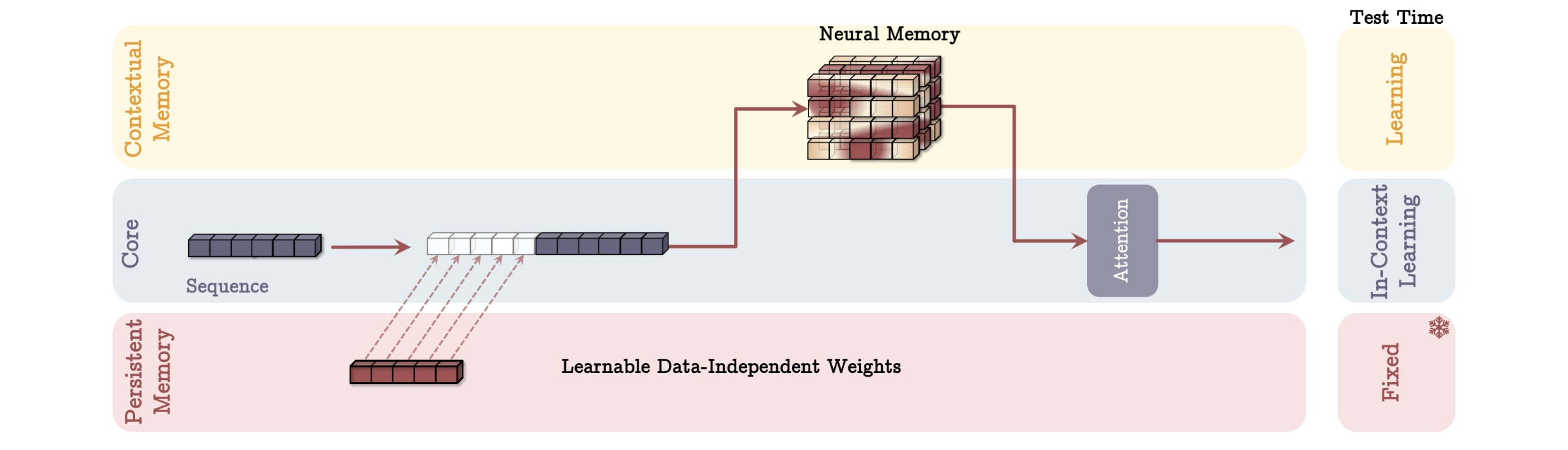
4 How to Incorporate Memory?
위에서 소개한 ‘neural memory’를 neural network에 incorporate하는 3가지 방법을 제시함 → 논문에서는 기존 neural network를 short-term memory modules라고 표현하면서, 특히 transformer는, key value를 누적하기 때문에 long context에서는 한계가 있다고 언급 → 하지만 제안하는 memory module을 memory에 read/write하면서 current key/value representation을 강화
→ 아래 모든 framework에서 core를 neural network/lm정도로 생각하고 따라가면 된다.
→ 또한 아래의 모든 framework가 test time에 어떻게 동작하는지를 기준으로 따라가자.
4.1 Memory as a Context (MAC)
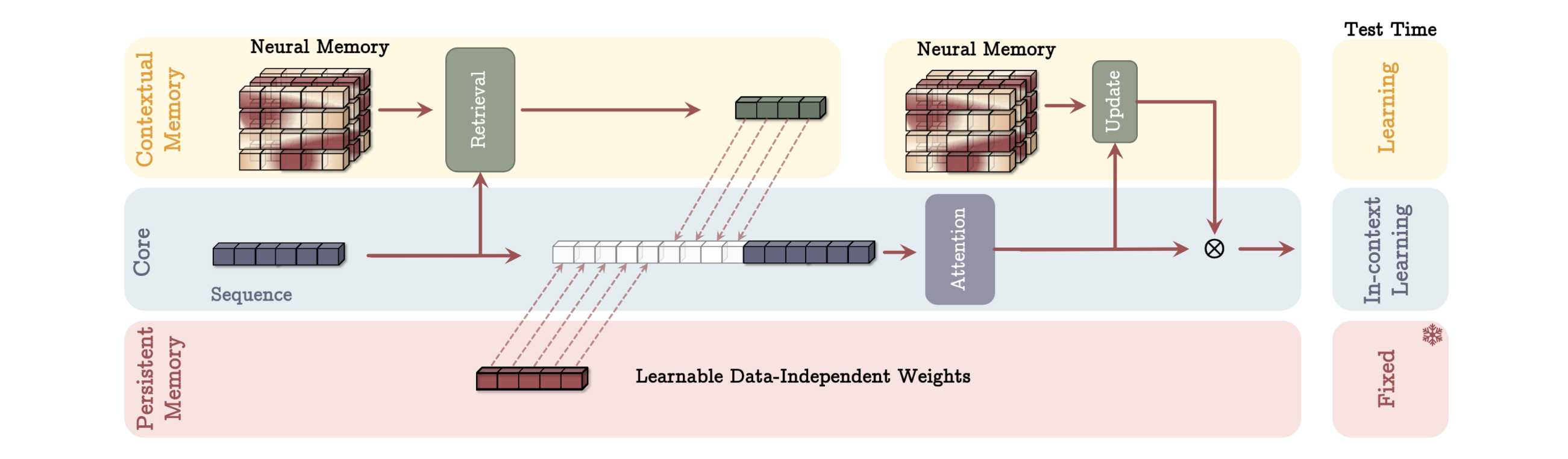
→ S^{(i)} \ (i = 1,\ldots,N/C) : sequence를 고정 크기 세그먼트만 처리하는 시스템
-
ht = \mathcal{M}{t-1}^*(\mathbf{q}_t) : memory module에서 고정 세그먼트와 유사한 past information retrieve
-
\tilde{S}^{(t)} = [p_1 \quad p_2 \quad \cdots \quad p_{N_p}] h_t S^{(t)} \ y_t = \text{Attn}(\tilde{S}^{(t)}) : persistent memory, past information, 고정 segment를 neural network에 forwarding해서 attention
→ attention은 standard attention과 동일함
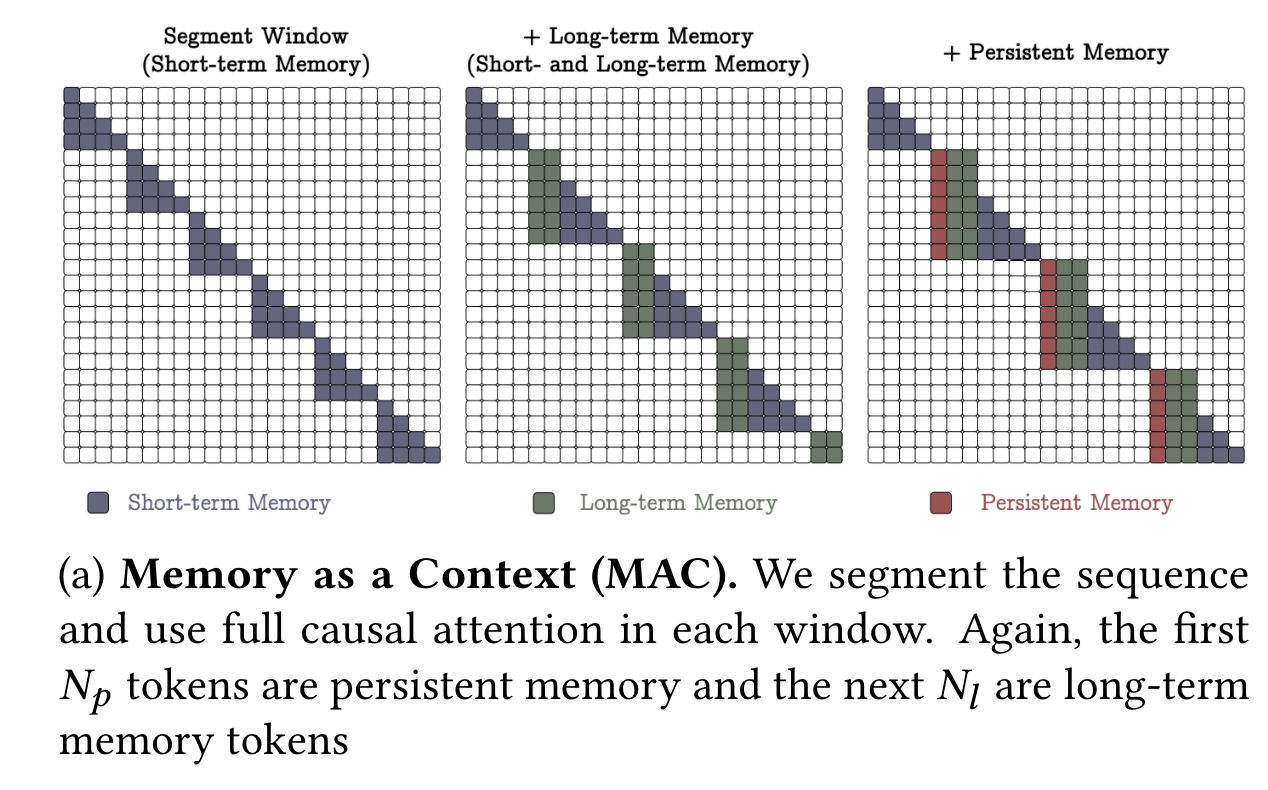
→ 세그먼트별로 persistent memory, past information가 추가됨에 따라 attention window만 길어지는 것을 알 수 있음
-
\mathcal{M}t = \mathcal{M}{t-1}(y_t) : attention output을 활용해 long-term memory module을 update
-
o_t = y_t \otimes \mathcal{M}_t^*(y_t) : update되 memory module에 attention output을 통과한 후 이를 기존 attention output과 tensor곱 연산 해 최종 output 계산
⇒ 해당 구조의 가장 큰 장점은 attention이 current/longterm에 동시에 attention을 주기 때문에 어떤 정보가 유용한지 파악 후 메모리 용량을 관리하기에 용이하다는 것
4.2 Gated Memory (MAG)
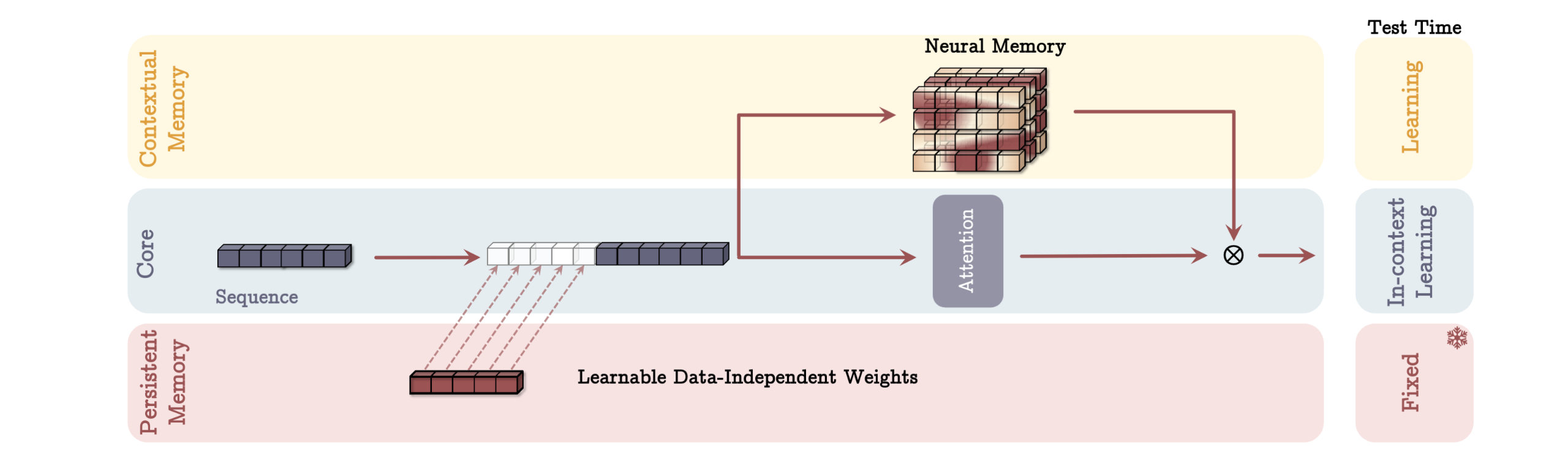
→ 이전처럼 memory module이 current input에 의해 update되긴 하지만 attention에 활용되지는 않음
-
\tilde{x} = [p_1 \quad p_2 \quad \cdots \quad p_{N_p}] x - y = \text{SW-Attn}^*(\tilde{x}) : sliding window attention으로 attention 처리
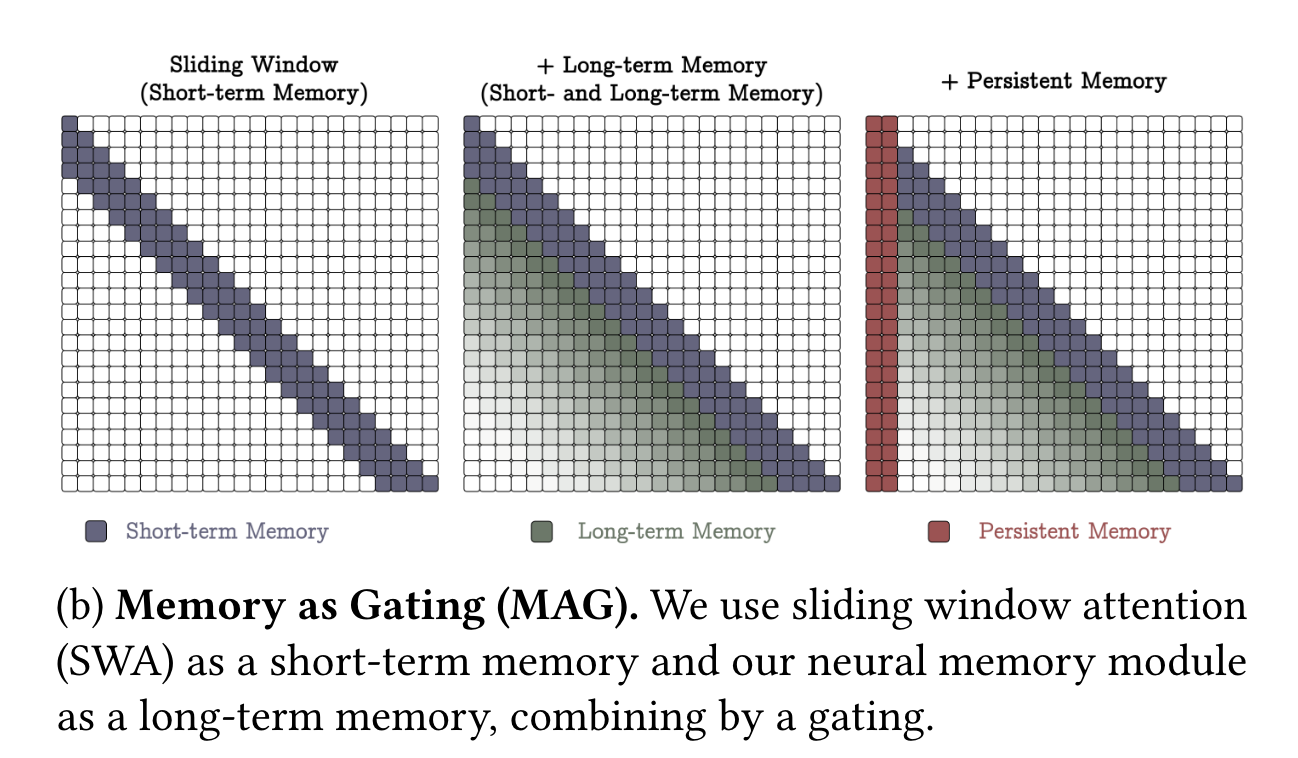
- o = y \otimes \mathcal{M}(\tilde{x})
→ y \ 와 \mathcal{M}(\tilde{x})의 output을 학습 가능한 벡터 값 가중치를 사용하여 정규화한 후 \sigma(\cdot) 적용 후 비선형 게이팅을 통해 최종 output을 만듦
→ (그리고 이게 아마 몇개의 layer로 쌓일 것이기 때문에) 그림에서 long-term memory는 fading의 형태로 attention map에 나타남. 반면, 다른 memory module은 precise하게 attention이 들어감.
4.3 Memory as a Layer (MAL)
→ attention과 neural memory module이 본인들이 설계한 의도를 100% 활용하지 못하도록 설계된 구조.
-
\tilde{x} = [p_1 \quad p_2 \quad \cdots \quad p_{N_p}] x -
y = \mathcal{M}(\tilde{x})
- o = \text{SW-Attn}(y)
→ attention의 장점을 활용못하니 attention 부분을 neural memory module로 바꾼 LMM로 또 다른 실험을 해봤다고 함.
5. Experiments
5.1 Experimental Setup
-
Models
-
scale: (i) 170M, (ii) 340M, (iii) 400M, and (iv) 760M parameters. (memory module + core를 의미하는 듯, MAC, MAG, MAL의 크기가 위와 같다고 하는것으로 보아)
-
training dataset: FineWeb-Edu dataset (i)~(iii)- 15B / (iv) - 30B
-
-
Training
-
max_lengths: 4K tokens.
-
batch_size: 0.5M tokens
-
5.2 Results - Language Modeling
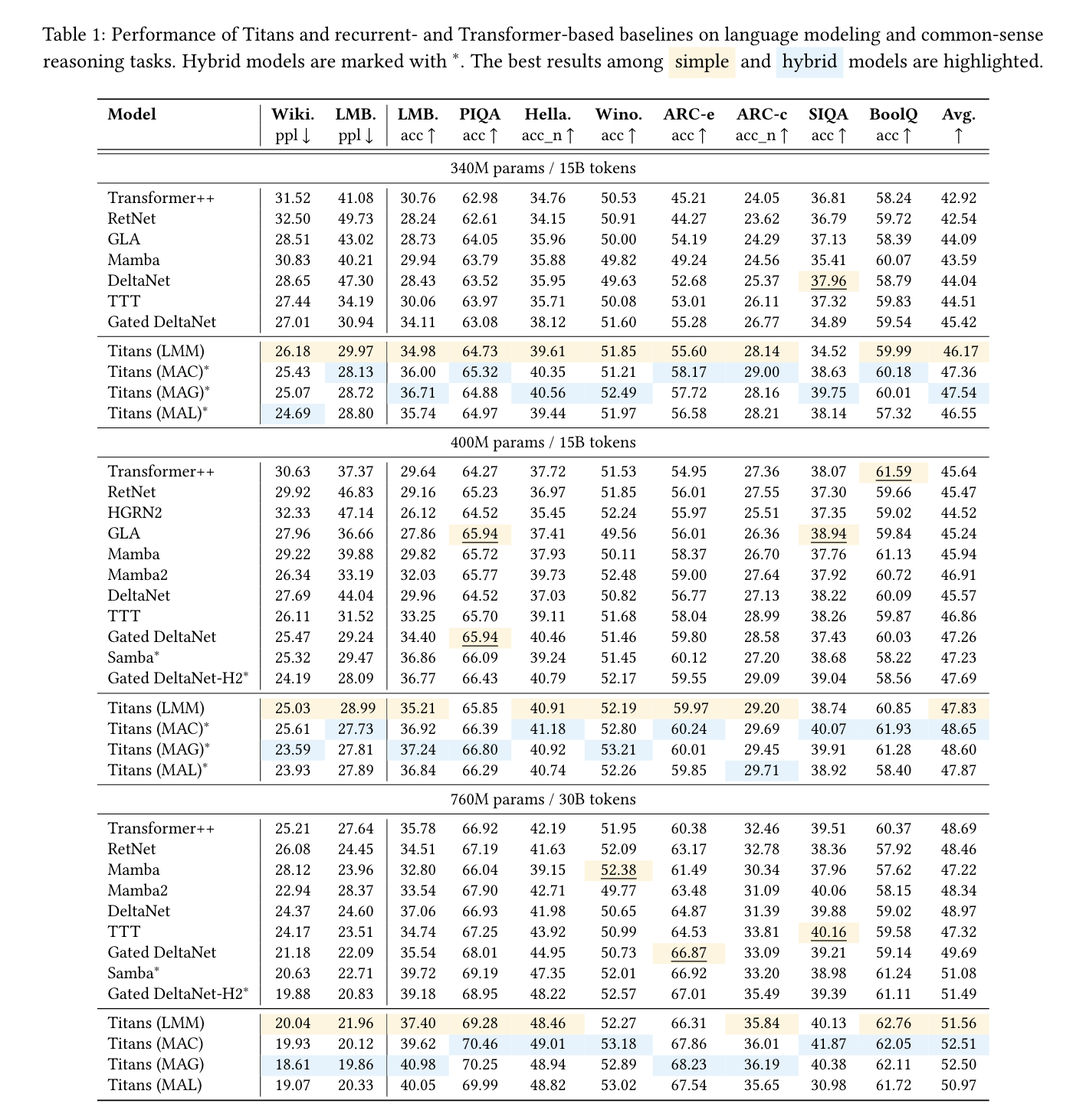
→ attention이 들어간 모델: hybrid model → *표기
→ attention을 안썼는데 가장 성능이 좋은 model → model
→ attention을 활용했는데 가장 성능이 좋은 model → model
-
Titan이 전반적으로 성능이 가장 좋다.
-
Mamba, Mamba2, and Gated DeltaNet도 gating mechanism을 쓰지만 본인들의 neural & deep memory가 더 효용이 높다고 하는데 attention 때문에 잘나온게 아닌가?라는 듦.
→ 그래서 Samba (Mamba + attention) and Gated DeltaNet-H2 (Gated DeltaNet + atttention)보다도 성능이 좋기 때문에 본인들이 powerful neural memory module를 잘 구축한 프레임워크를 만들었다고 주장
- 구조상 메모리를 가져와서 attention하고 update하는 MAC이 long sequence data에 대한 dependency가 강하다고 함
5.2 Results - Needle in a Haystack
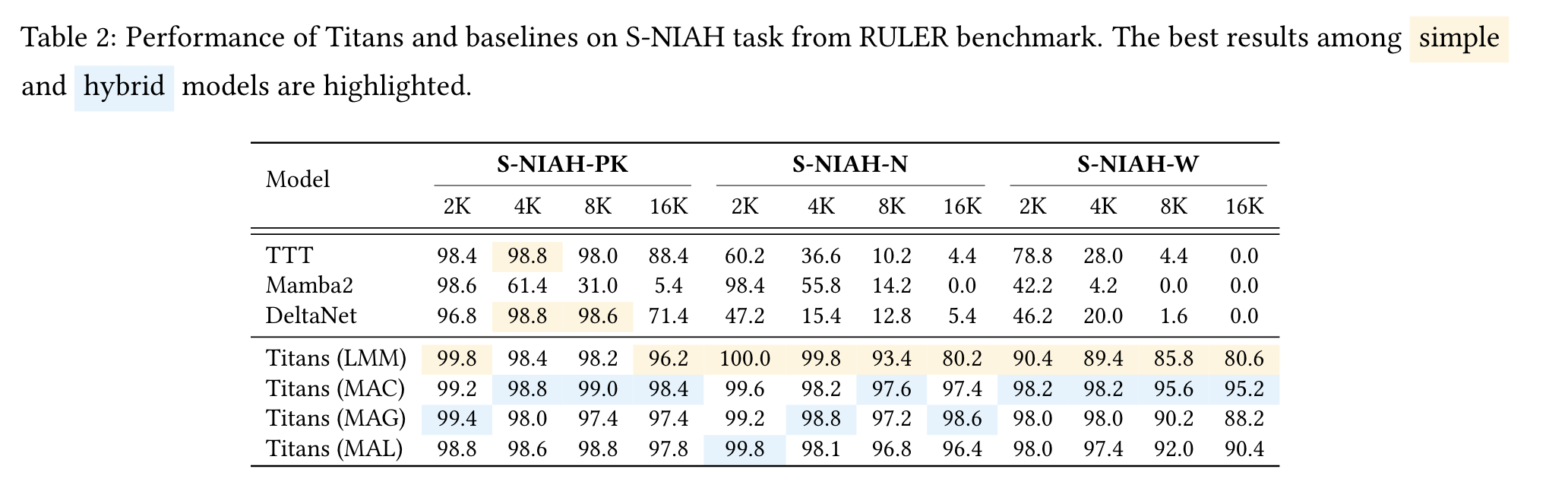
-
TTT에 비해서는 momentum과 forgetting mechanism이 있어서 유연한 memory module 관리가 가능
-
forgetting mechanism가 있는 Mamba2에 비해서는 deep non-linear 구조를 가지고 있기 때문에 보다 더 효용성 높은 memory module 관리가 가능
⇒ 가장 long context handling 능력을 많이 요구하는 S-HIAH task에서 성능이 좋다.
5.2 Results - The Effect of Deep Memory
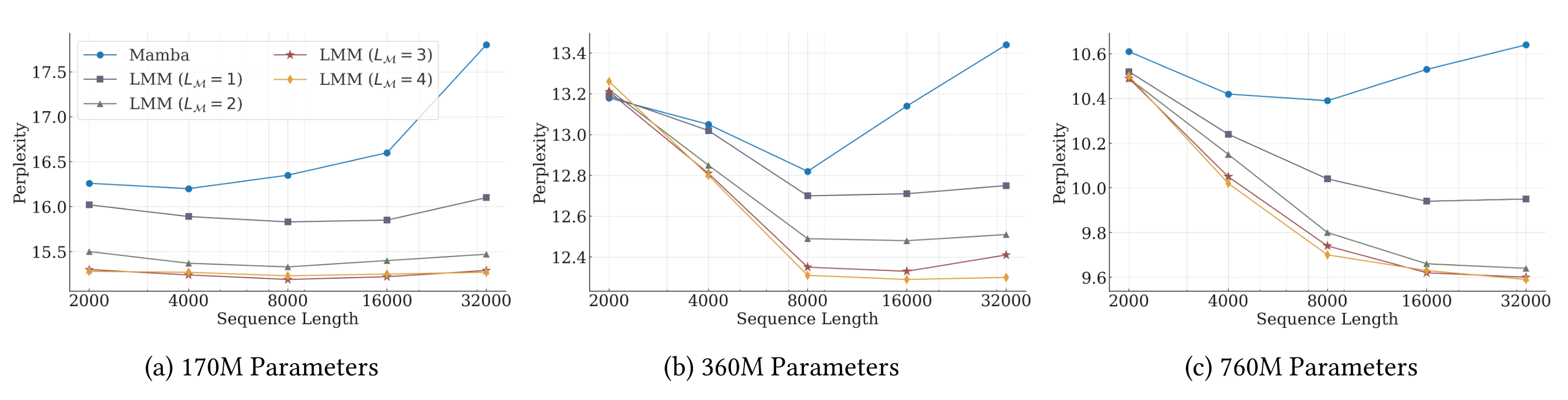
→ memory module로만 구조를 짜도 Mamba보다 long context 대한 ppl이 떨어짐
→ memory module depth만 올려도 ppl이 떨어지며, 모델 파라미터를 키울수록 긴 길이에 대한 ppl이 덜어짐
5.2 Results - Time Series & DNA Modeling
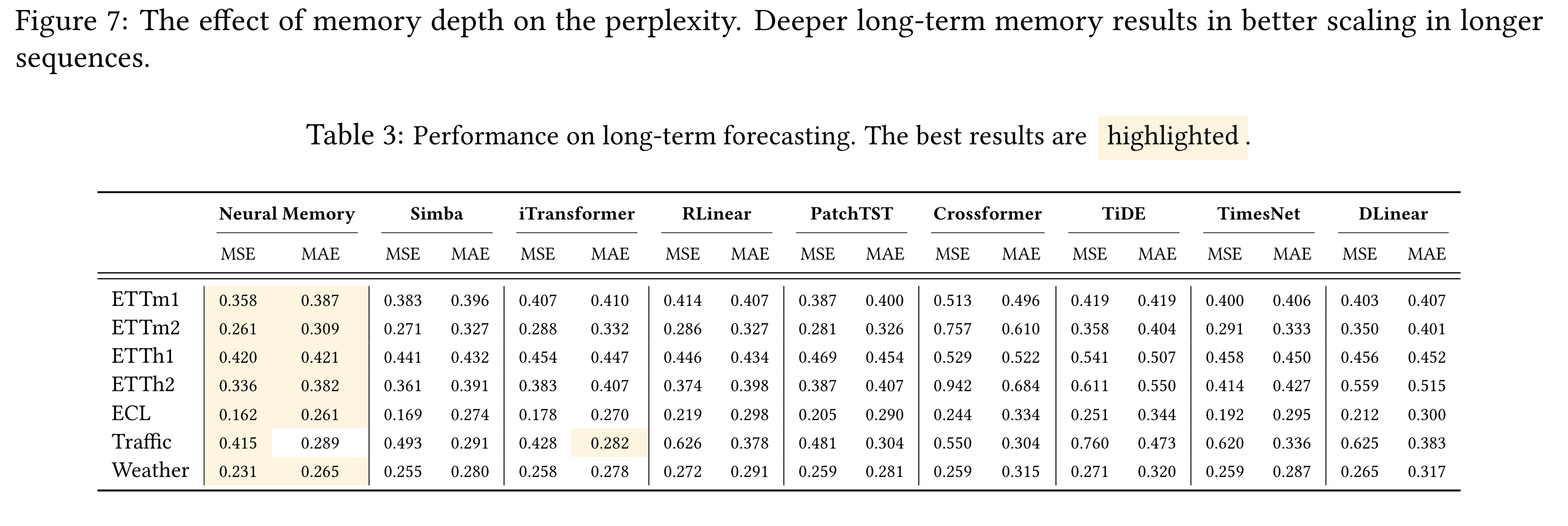
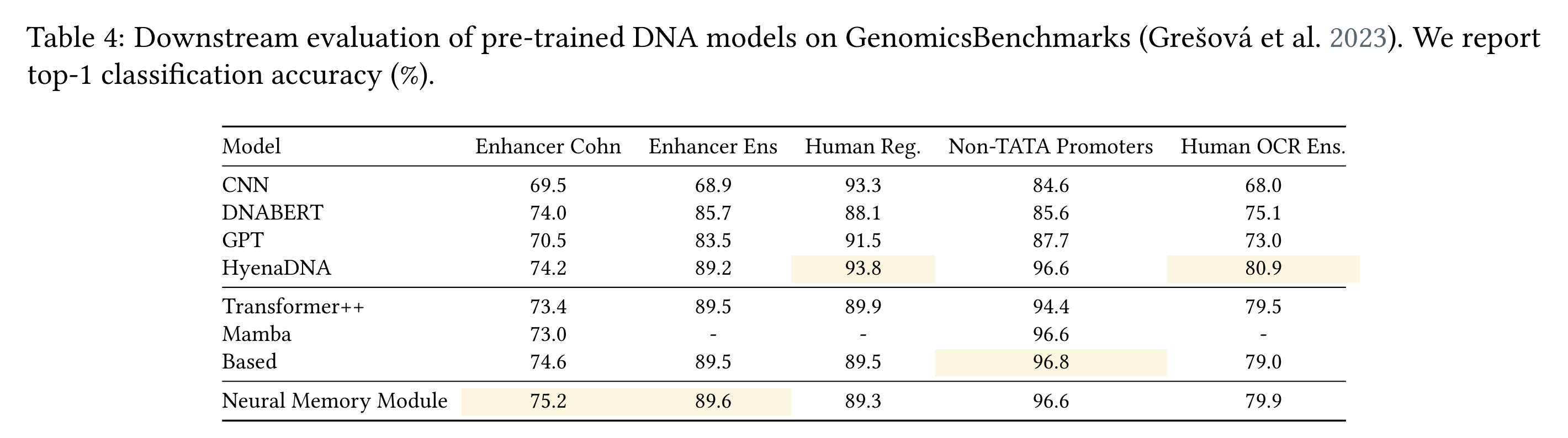
→ (위) Mamba module를 neural memory로 대체했더니 잘 나오더라
→ (아래) DNA modeling task에서도 성능 잘 나오더라
5. Conclusion
-
test time때 memory module을 read/write하는 meta in-context learner를 만들고자 했던거 같음
-
attention을 통해 모든 knowledge를 기억하는게 아니라 pre-training때 일부 knowledge는 학습시켜놓고, inference/forwarding되면서 필요한 memory를 관리하는 시스템을 만들고자 하는게 이 논문의 최종 목표가 아니었을까?라는 생각이 듦.