WHEN IS TASK VECTOR Provably EFFECTIVE FOR MODEL EDITING? A GENERALIZATION ANALYSIS OF NONLINEAR TRANSFORMERS
논문 정보
- Date: 2025-03-11
- Reviewer: hyowon Cho
1. Intro
LLM의 학습 연산 및 메모리 비용 문제를 해결하기 위한 방법론으로 대표적인 것은 PEFT이지만, 간혹 Task Vector를 이용한 접근법들이 등장하고 있다.
태스크 벡터 기법은 다음과 같이 작동한다:
-
단순한 태스크에서 사전 학습 모델을 미세 조정하여 태스크 벡터를 생성 → 이는 미세 조정된 모델과 사전 학습 모델 간의 가중치 차이를 나타냄.
-
보다 복잡한 태스크를 처리하기 위해 여러 태스크 벡터를 선형 조합하여 모델을 수정 → 복잡한 태스크에 대한 추가 미세 조정 없이 효율적인 적응이 가능함.
이 방법은 선형 조합만으로도 다양한 다운스트림 태스크에 적응할 수 있는 장점이 있으며, 다음과 같은 특성을 보인다:
-
태스크 벡터 추가 → 해당 태스크 성능 향상
-
태스크 벡터 제거 → 특정 태스크의 지식 제거 (unlearning)
-
적절한 조합 → 라벨 데이터 없이도 유사한 관계를 가진 새로운 태스크(out-of-domain task)에 일반화 가능
-
또한, 저차원(low-rank) 또는 희소(sparse) 태스크 벡터를 사용하면 성능을 유지하면서도 효율성을 더욱 향상할 수 있음
태스크 벡터의 실용적 성공에도 불구하고, 이에 대한 이론적 분석은 아직 충분하지 않음. 특히, 다음과 같은 질문이 제기된다:
태스크 벡터가 멀티태스크 학습, unlearning, 및 out-of-domain generalization를** *****언제, 왜*** 성공적으로 수행할 수 있는가?
오늘 소개할 논문은 비선형 Transformer 모델에서 태스크 벡터(task arithmetic)의 이론적 일반화 분석을 최초로 수행하며, multi-task learning, unlearning, out-of-domain generalization에 대한 이론적 근거를 제공한다.
특히, binary classification 태스크를 대상으로 태스크 벡터 효과가 산술적 하이퍼파라미터(arithmetic hyperparameters)에 어떻게 의존하는지를 정량적으로 분석한다.
비록 분석은 단순화된 단일 헤드(single-head) 및 단일 층(one-layer) 비선형 Transformer을 기반으로 하지만, 이론적 통찰은 실제 아키텍처에서도 검증된다.
(건우 연구에 태스크 벡터가 활용된다고 들어서, 선행 연구 참고용으로 가져왔습니다🙌)
논문의 contribution은 다음과 같다:
- task addition 및 task negation에 대한 세밀한 특성 학습 분석
-
태스크 추가(task addition)
- 태스크 간 연관성이 없거나(aligned) 서로 긍정적인 영향을 미치는 경우 멀티태스크 학습이 효과적으로 수행됨.
-
태스크 제거(task negation)
- 태스크가 무관(irrelevant)하거나 상충(contradictory)할 경우, 즉 한 태스크의 성능 향상이 다른 태스크의 성능 저하를 초래하는 경우, 태스크 제거가 효과적임.
- 태스크 벡터를 활용한 out-of-domain generalization에 대한 최초의 이론적 보장 제공
-
연관성이 없는 태스크들의 태스크 벡터 집합을 활용하여 적절한 산술 계수(arithmetic coefficients)를 선택하면 다양한 새로운 태스크에 일반화할 수 있음을 증명.
-
일반화를 위해 필요한 적절한 산술 계수의 범위를 특성화.
- 태스크 벡터의 low-rank approximation 및 magnitude-based pruning에 대한 이론적 정당화
- 태스크 벡터의 저차원 및 희소(sparse) **근사가 **일반화 성능에 미치는 영향을 최소화할 수 있음을 증명.
Related Works
Weight interpolation technique
-
가중치 보간 또는 모델 병합(model merging)은 여러 모델의 가중치를 선형적으로 보간(interpolation) 하는 기법
-
이 기법은 서로 다른 다운스트림 태스크에서 미세 조정된 모델 또는 다른 하이퍼파라미터로 학습된 모델을 병합하는 방법으로 활용됨 (model soups)
-
실험적으로, 가중치 보간은 모델을 더 넓은 최적점(wider optima)으로 유도하여 일반화 성능을 향상할 수 있으며 단일 태스크(single-task) 및 멀티태스크(multi-task) 성능에서 기존 미세 조정(fine-tuning) 방법을 능가할 수도 있음.
-
태스크 벡터 접근법은 이러한 가중치 보간의 특수한 형태로 볼 수 있으며, 태스크 벡터에 대한 선형 연산(linear operations)을 수행하는 방식.
Feature learning analysis for Transformers.
-
최근 연구들은 Transformer의 최적화 및 일반화 성능을 특성 학습(feature learning) 관점에서 분석.
-
신경망이 학습 과정에서 중요한 특징을 점차적으로 학습하고, 불필요한 특징을 배제하는 과정을 설명하는 프레임워크를 따름.
-
하지만, 병합된 모델에 대한 논의는 전혀 이루어지지 않음
2. TASK VECTOR: DEFINITION AND OBSERVATIONS
2.1 PRELIMINARIES
신경망 f: X \times \Theta \to Y 는 입력 X \in X 를 받아 출력 y \in Y 를 생성하며, \Psi \in \Theta 는 모델의 파라미터를 나타낸다.
-
\Psi^{(0)}: 사전 학습된(pre-trained) 모델
-
\Psi^*_T: 특정 태스크 T 에 대해 미세 조정된(fine-tuned) 모델
태스크 벡터(Task Vector) 정의
정의 1. 태스크 T 에 대한 **태스크 벡터 **\Delta \Psi_T 는 사전 학습 모델과 미세 조정 모델 간의 가중치 차이로 정의됨:
\Delta \Psi_T = \Psi^*_T - \Psi^{(0)}
즉, 특정 태스크에 대한 모델의 변화량을 나타내는 벡터임.
Task Arithmetic과 일반화
-
주어진 사전 학습 모델 \Psi^{(0)}와 여러 태스크 벡터 { {\Delta \Psi{T_i}}{i \in V}}를 사용하여 병합된 모델(merged model) 을 구성할 수 있음:
-
\Psi = \Psi^{(0)} + \sum{i \in V} \lambda_i \Delta \Psi{T_i}
-
여기서 \lambda_i 는 태스크 벡터의 가중치.
-
-
손실 함수 l(X, y; \Psi) 를 사용하여 태스크 **T′** 에 대한 일반화 오류는 다음과 같이 정의됨:
- \mathbb{E}{(X,y) \sim D{T’}} l(X, y; \Psi)
-
멀티태스크 학습 (Multi-Task Learning)
-
태스크 벡터를 추가( λi>0 )하면, 해당 태스크들의 성능을 유지하면서 동시에 학습 가능:
-
\mathbb{E}{(X,y) \sim D{T_i}} l(X, y; \Psi) \leq \Theta(\epsilon), \quad \forall i \in V_A
-
멀티태스크 학습이 성공했을 때, 모델 Ψ가 모든 태스크 Ti 에 대해 일정 수준 이하의 일반화 오류(Θ(ϵ) )를 유지함을 의미
-
-
-
학습 제거 (Unlearning)
- 특정 태스크 벡터를 부호 반전( λi<0 )하여 제거하면, 해당 태스크의 성능이 저하됨: \mathbb{E}{(X,y) \sim D{T_i}} l(X, y; \Psi) \geq \Theta(1), \quad \forall i \in V_N
\mathbb{E}{(X,y) \sim D{T_j}} l(X, y; \Psi) \leq \Theta(\epsilon), \quad \forall j \in V \setminus V_N
-
도메인 외 일반화 (Out-of-Domain Generalization)
-
태스크 벡터를 활용하여 새로운 태스크에 일반화 가능: \Delta \Psi{T’} = \Delta \Psi{TA} + (\Delta \Psi{TB} - \Delta \Psi{T_C})
-
이는 특정 태스크 벡터 조합을 사용하여 유사한 관계를 가진 새로운 태스크에 적용할 수 있음을 의미함.
-
2.2 EMPIRICAL OBSERVATIONS
Colored-MNIST 데이터셋을 활용하여 태스크 간 관계를 분석
-
무관한 태스크 (Irrelevant Tasks)
- 한 데이터셋에서는 홀수/짝수 분류가 빨강/초록 색과 강하게 연관되지만, 다른 데이터셋에서는 색과 무관.
-
정렬된 태스크 (Aligned Tasks)
- 두 데이터셋 모두 홀수/짝수 분류가 빨강/초록 색과 같은 방식으로 연관.
-
상충하는 태스크 (Contradictory Tasks)
- 두 데이터셋에서 홀수/짝수 분류와 색의 관계가 정반대.
모델 평가 방식
- 두 개의 태스크 T1 과 T2 를 고려하여, 모델 \Psi = \Psi^{(0)} + \Delta \Psi{T_1} + \lambda \Delta \Psi{T_2} 의 성능을 측정.
주요 실험 결과 1

-
무관한 태스크 (Irrelevant Tasks)
- 멀티태스크 학습과 학습 제거가 모두 우수함
-
정렬된 태스크 (Aligned Tasks)
-
멀티태스크 학습 성능이 좋음
-
하지만 학습 제거(Unlearning) 성능은 낮음
-
-
상충하는 태스크 (Contradictory Tasks)
-
학습 제거(Unlearning) 성능이 매우 뛰어남
-
그러나 멀티태스크 학습 성능이 저조함
-
그렇다면 질문이 생긴다:
💡 핵심 질문(Q1): 태스크 간의 상관관계가 멀티태스크 학습과 학습 제거 성능에 미치는 영향은 어떻게 정량적으로 측정될 수 있는가?
주요 실험 결과 2
-
Colored-MNIST를 이용해 새로운 태스크 T′ 를 구성
- T′는 T1 과 정렬된 태스크, T2와 상충하는 태스크
-
\lambda1, \lambda_2를 최적화하여 \Psi = \Psi^{(0)} + \lambda_1 \Delta \Psi{T1} + \lambda_2 \Delta \Psi{T_2} 를 학습
-
실험 결과, 적절한 λ1,λ2 선택 시 개별 미세 조정된 모델보다 뛰어난 성능을 보임

💡 핵심 질문(Q2): 태스크 벡터 연산이 도메인 외 일반화에서 효과적인 이유는 무엇이며, 최적의 λi 를 선택하는 방법은 무엇인가?
3. A DEEP DIVE INTO TASK VECTORS
💡 핵심 질문(Q1): 태스크 간의 상관관계가 멀티태스크 학습과 학습 제거 성능에 미치는 영향은 어떻게 정량적으로 측정될 수 있는가?
💡 핵심 질문(Q2): 태스크 벡터 연산이 도메인 외 일반화에서 효과적인 이유는 무엇이며, 최적의 λi 를 선택하는 방법은 무엇인가?
이제 제안된 질문들을 해결함과 동시에
-
태스크 벡터를 수학적으로 formulate하고
-
멀티 태스크, 언러닝, OOD에 대한 이론적 분석을 수행해봅시다
-
또한, low-rank approximation & sparsification 방법이 성능을 유지하면서 계산 비용을 줄일 수 있음을 증명한다.
3.1 Main Theoretical Insights
이 연구에서는 이진 분류(binary classification) 태스크 집합을 다룬다.
-
각 태스크의 레이블(label)은 판별적 토큰(discriminative tokens)과 그 반대되는 토큰(opposite tokens) 간의 다수결(majority voting)로 결정됨.
-
단일 층(one-layer) 및 단일 헤드(single-head) Transformer 모델을 분석 대상으로 함.
Major takeaways:
-
P1. 태스크 추가(Task Addition) 및 제거(Task Negation)의 정량적 분석
-
태스크 T1 과 T2 간의 상관관계(correlation) α 를 정의:
-
α>0 → 정렬된(aligned) 태스크
-
α<0 → 상충하는(contradictory) 태스크
-
α=0 → 무관한(irrelevant) 태스크
-
-
멀티태스크 학습이 성공적으로 수행되는 조건
-
\lambda \geq 1 - \alpha + \beta (여기서 β 는 작은 상수)
-
학습 제거(unlearning)이 성공하는 조건
- **무관한 태스크의 경우**: \lambda \leq 0 - **상충하는 태스크의 경우**:\lambda \in [-\Theta(\alpha^{-2}), O(\alpha^{-1})]
-
P2. Out-of-Domain Generalization through Task Arithmetic
-
기존 태스크 Ti 와 타겟 태스크 T′간의 상관관계 **\gamma_i** 를 정의.
-
만약 모든 Ti 가 T′ 와 완전히 무관하지 않다면, 적절한 태스크 벡터 조합을 통해 도메인 외 일반화가 가능함을 증명.
-
일반화 성능을 보장하기 위해 산술적 하이퍼파라미터(arithmetic hyperparameter)를 **\gamma_i** 의 함수로 정량적으로 도출.
-
-
P3. Low-Rank Approximation 및 Magnitude-Based Pruning가 모델 editing 성능을 유지함
-
태스크 벡터를 저차원 근사 또는 희소화하여 계산 비용을 줄이는 기법이 일반화 성능을 보장함을 최초로 이론적으로 증명.
-
MLP 층에서 태스크 벡터의 작은 크기의 행(rows with small magnitudes)을 제거하여 희소화 가능.
-
3.2 PROBLEM FORMULATION
데이터 및 모델 정의
-
데이터 X = (x_1, x_2, \dots, x_P) \in \mathbb{R}^{d \times P}는 P 개의 토큰을 포함하며,
-
각 토큰 x_i 는 d-차원의 벡터이고,
-
모든 토큰은 단위 노름을 가짐 (∥xi∥=1).
-
-
레이블 y∈{+1,−1} 는 스칼라 값.
Transformer 모델 구조
본 연구에서는 단일 층 Transformer을 사용하며, 모델은 self-attention 레이어 1개와 2층 MLP으로 구성됨.
수학적으로 모델은 다음과 같이 표현된다:
f(X; \Psi) = \frac{1}{P}\sum{l=1}^P a^\top \text{ReLU}(W_O \sum{l=1}^P W_V x \cdot \text{softmax} (x^\top W_K^\top W_Q x))
여기서,
-
\Psi = { {a^{(l)}}_{l=1}^{P}, W_O, W_V, W_K, W_Q } 는 모델의 모든 파라미터 집합.
-
a^{(l)} \in \mathbb{R}^{m} 및 W_O \in \mathbb{R}^{m \times m_a} 는 MLP 계층의 가중치.
**Fine-tuning Algorithm **
-
손실 함수로 Hinge Loss 사용함:
-
SGD 사용하여 모델을 fine-tuning
-
a^{(l)}_i 는 {+1/\sqrt{m}, -1/\sqrt{m}} 에서 샘플링됨.
-
Fine-tuning 동안 **a^{(l)}**는 업데이트되지 않음.
데이터 생성 과정 (Definition 2: Data Formulation)
데이터 X는 여러 개의 토큰 x1,x2,…,xP로 이루어진다.
각 토큰은 d차원의 벡터이고, X \in \mathbb{R}^{d \times P}이다.
레이블 y는 {+1,−1}중 하나이며, 이진 분류 문제이다.
이때, 각 태스크 T는 특정한 패턴(=판별적 정보, discriminative pattern) **\mu_T**를 가진다.
이 패턴은 레이블을 결정하는 데 중요한 역할을 하는 특수한 벡터라고 보면 된다.
1. 레이블 y정하기
- y=+1 또는 y=−1 중에서 랜덤하게 선택한다. (즉, 데이터를 반반 확률로 양성(+) 또는 음성(-) 샘플로 정함)
2. 데이터 X 만들기
데이터 X는 P개의 토큰으로 이루어져 있다.
각 토큰은 다음 중 하나가 된다:
- 판별적 패턴(Discriminative Pattern): \mu_T 또는 −\mu_T
-
이 패턴은 레이블과 관련이 있다.
-
y=+1 이면, μT 가 더 많이 등장한다.
-
y=−1 이면, −μT 가 더 많이 등장한다.
-
(예: “고양이”를 분류하는 태스크라면, μT 는 “고양이 관련 특징”을 포함하는 벡터라고 볼 수 있음)
- 태스크 무관(irrelevant) 토큰: v1,v2,…,vM
-
이 토큰들은 레이블과 무관하다.
-
vj들은 μT 와 직교(orthogonal)한 랜덤 벡터들이다.
-
(예: “고양이” 태스크와 무관한 “날씨” 관련 단어들처럼, 분류할 때 필요하지 않은 정보)
3. 토큰 구성 비율
각 샘플에는 다음과 같이 세 종류의 토큰이 포함됨:
-
레이블 관련 토큰 (Label-Relevant Tokens, μT): 전체 토큰 중 비율이 δ∗
-
혼동 패턴 (Confusion Pattern, −μT): 비율이 δ#
-
태스크 무관 토큰 (Task-Irrelevant Tokens, vj): 비율이 (1 - \delta^* - \delta^#)/M
즉, 레이블을 결정하는 핵심 토큰( μT,−μT)과 그렇지 않은 토큰(vj)이 섞여 있는 구조다.
- **예제**
예제 1: 동물 사진 분류
-
태스크: 개 🐶 vs 고양이 🐱 분류
-
판별적 패턴: 개를 나타내는 특징 벡터 μT (예: 귀 모양, 꼬리 형태)
-
태스크 무관 토큰: 배경 색상, 카메라 화질 등 (이것들은 개/고양이를 구별하는 데 영향을 주지 않음)
데이터 생성 과정
-
사진 한 장을 랜덤으로 뽑고, 개인지 고양이인지 결정 (y)
-
개의 사진이라면, “개 관련 특징( μT )”이 더 많이 포함됨
-
고양이 사진이면, “고양이 관련 특징( −μT )”이 더 많이 포함됨
-
배경이나 조명 같은 “무관한 특징( vj )”들도 포함됨
🎯 예제 2: 감성 분석 (Positive vs Negative)
-
태스크: 영화 리뷰가 긍정적인지( y=+1 ) 부정적인지( y=−1 ) 분류
-
판별적 패턴: 긍정적인 단어들( μT ) vs 부정적인 단어들( −μT )
-
태스크 무관 토큰: 영화 제목, 감독 이름 등 감성 분석과 관계없는 단어들
데이터 생성 과정
-
리뷰 하나를 선택하고, 긍정( y=+1 )인지 부정( y=−1)인지 랜덤 결정
-
긍정 리뷰라면, “좋아요”, “재밌어요” 같은 긍정적인 단어( μT )가 더 많이 포함됨
-
부정 리뷰라면, “별로였어요”, “실망했어요” 같은 부정적인 단어( −μT )가 더 많이 포함됨
-
감독 이름 같은 감성 분석과 상관없는 단어( vj )들도 포함됨
3.3 HOW DO TASK ADDITION AND NEGATION AFFECT THE PERFORMANCE?
1. 문제 설정
-
두 개의 이진 분류 태스크 T1, T2 를 고려
-
각 태스크의 판별적 패턴(Discriminative Pattern):
-
\mu_{T_1} (태스크 T1 의 특징)
-
\mu_{T_2} (태스크 T2 의 특징)
-
-
태스크 벡터: \Delta \Psi{T_1}, \Delta \Psi{T_2}
-
모델 병합: \Psi = \Psi^{(0)} + \Delta \Psi{T_1} + \lambda \Delta \Psi{T_2}
-
태스크 간의 상관관계( α ) 정의: \alpha = \mu{T_1}^\top \mu{T_2} \in [-1,1]
- α>0: **정렬된(aligned) 태스크** - α<0: **상충하는(contradictory) 태스크** - α=0: **무관한(irrelevant) 태스크**
-
-
실험적으로 도출된 추가 변수 (설명은 x):
-
\beta = poly(\eta \delta^*) + \Theta(\epsilon \sqrt{M}) (< \Theta(1))
-
뉴런 수: m \gtrsim M^2 \log M(여기서 M=Θ(d))
-
설명
-
β 는 두 개의 주요 항목으로 구성됨:
1. **poly(\eta \delta^*)**** : 학습률(η)과 태스크의 판별적 정보량(****\delta^*****)에 의해 결정되는 다항식(poly) 항목**
- δ∗ 는 **레이블과 직접적인 관련이 있는 토큰(판별적 패턴, μT)의 비율**을 의미함.
- 즉, 이 값은 **태스크의 난이도(task difficulty) 및 학습률(learning rate)과 관련됨**.
- **δ∗ 가 클수록, 즉 중요한 패턴이 많이 포함될수록 모델이 더 빠르게 수렴할 가능성이 높음.**
1. **\Theta(\epsilon \sqrt{M})**** : 일반화 오류(ϵ)와 데이터 차원(M)에 의해 결정되는 항목**
- M 은 데이터 차원의 크기 (M=Θ(d))
- 이 항목은 **모델의 일반화 성능(generalization performance)과 관련됨**.
- 차원이 클수록 \sqrt{M}이 증가하므로, **차원이 높을수록 일반화 오류가 증가할 가능성이 있음**.
\beta < \Theta(1)**의 의미**
- **β값이 너무 크면, 태스크 벡터를 추가하거나 제거할 때 오류가 크게 증가하므로 모델이 원하는 성능을 내지 못할 수 있음.**
- 따라서 β 가 일정 수준 이하(<Θ(1))로 유지되면, **태스크 벡터 추가/제거 시 성능이 안정적으로 유지될 수 있음**.
Theorem 1 (멀티태스크 학습 성공 조건)
주어진 사전 학습 모델을 태스크 T1 및 T2 에 대해 미세 조정한 후, 모델 병합이 성공하기 위한 조건은 다음과 같다:
- 미세 조정 시 필요한 조건 3가지:
-
충분한 배치 크기(Batch Size) 필요:
-
** **B \geq \Omega(\epsilon^{-2} \log M)
-
배치 크기 B 가 충분히 커야 함.
-
배치 크기가 작으면 모델이 안정적으로 학습되지 않아 태스크 벡터가 제대로 형성되지 않을 수 있음.
-
일반적으로 \epsilon^{-2} \log M만큼의 배치 크기를 확보하면, 모델이 충분히 학습 가능.
-
-
적절한 학습률(Learning Rate)
-
** \eta \leq O(1)**
-
학습률 η 가 너무 크면 학습이 불안정해지고, 너무 작으면 학습이 지나치게 오래 걸릴 수 있음.
-
따라서, O(1) (즉, 적절한 크기의 상수) 이하로 학습률을 유지해야 함.
-
-
충분한 학습 반복 횟수(Training Iterations)
-
t \geq T = \Theta(\eta^{-1} \delta^{-2})
-
δ 델타는 태스크의 판별적 패턴( μT)을 포함하는 토큰의 비율을 나타냄.
-
학습 반복 횟수 t 가 충분히 커야 태스크 벡터가 제대로 학습됨.
-
반복 횟수는 학습률 η 와 태스크의 판별적 정보량 δ∗에 반비례.
-
δ∗ 가 클수록(즉, 중요한 패턴이 많이 포함될수록) 적은 반복 횟수로도 학습 가능.
-
δ∗가 작을수록(즉, 태스크 판별 패턴이 약할수록) 더 많은 반복이 필요함.
-
-
- 이 조건을 만족하면, 병합된 모델의 일반화 오류는 다음과 같이 유지됨:
-
태스크 T1의 일반화 오류
-
\mathbb{E}{(X,y) \sim D{T_1}} l(X, y; \Psi) \leq \Theta(\epsilon) + \lambda \cdot \beta -
즉, T1 에 대한 모델의 오류는 \Theta(\epsilon)** + 추가적인 항목( **** \lambda \cdot \beta ****)으로 구성됨**. -
( ** \lambda \cdot \beta **) 항목은 태스크 벡터 병합에 따른 추가적인 오류를 나타냄. -
β가 작을수록 멀티태스크 학습이 안정적임.
- 즉, λ값이 너무 크면 모델 성능이 불안정해질 수 있음.
-
-
-
태스크 T2 의 일반화 오류
-
\mathbb{E}{(X,y) \sim D{T_2}} l(X, y; \Psi) \leq \Theta(\epsilon)
-
즉, T2 에 대한 모델의 오류는 \Theta(\epsilon)**으로 유지됨.**
-
λ가 적절하게 선택되면 태스크 T2 에 대해 성능이 안정적으로 유지됨.
-
즉, 적절한 λ값이 설정되면, 두 태스크에서 모두 성능을 유지하면서 멀티태스크 학습이 가능하다!
- 멀티태스크 학습이 성공하기 위한 λ 의 조건
태스크 벡터 병합이 성공하려면, λ 를 적절하게 설정해야 한다.
-
λ 값이 너무 크면, ∣λ∣⋅β 항목이 커져서 특정 태스크의 오류가 증가할 수 있음. -
λ값이 너무 작으면, 태스크 벡터의 효과가 충분히 발휘되지 않을 수 있음.
-
즉, λ는 태스크 간의 관계( α)를 고려하여 최적의 값을 찾아야 한다.
- 무관한 태스크 (α=0)
\lambda \geq 1 - \beta
- **정렬된 태스크 (α>0)**
\lambda \geq 1 - \alpha + \beta
- **상충하는 태스크 (α<0)**
- **적절한 λ 를 선택해도 두 태스크의 일반화 오류를 모두 낮추는 것이 불가능**
- 즉, **상충하는 태스크에서는 멀티태스크 학습이 어렵거나 불가능**
정리!
-
태스크가 무관하거나 정렬된 경우, 적절한 λ 를 선택하면 멀티태스크 학습이 성공할 수 있음.
-
상충하는 태스크의 경우, 하나의 태스크 성능이 좋아질수록 다른 태스크의 성능이 나빠지므로 멀티태스크 학습이 불가능.
Theorem 2 (학습 제거 성공 조건)
-
태스크 T1의 일반화 오류
-
\mathbb{E}{(X,y) \sim D{T_1}} l(X, y; \Psi) \leq \Theta(\epsilon) + \lambda \cdot \beta
-
-
태스크 T2 의 일반화 오류
- \mathbb{E}{(X,y) \sim D{T_2}} l(X, y; \Psi) \ge \Theta(1)
즉, 모델\Psi는 태스크 T1 에 대한 성능을 유지하면서, T2 의 성능을 심각하게 저하시켜야 함.
학습 제거가 성공하기 위한 λ의 조건
- 무관한 태스크 (α=0)
\lambda \leq 0
- 상충하는 태스크 (α<0)
-\Theta(\alpha^{-2}) \leq \lambda \leq -poly(\eta \delta^*)/\alpha
-
정렬된 태스크 (α>0)
-
α가 작을 경우에만 적절한 λ가 존재
-
즉, 태스크 간 정렬 정도가 높을수록 학습 제거가 더 어려움
-
정리!
-
태스크가 무관하거나 상충하는 경우, 적절한 λ 를 선택하면 특정 태스크를 효과적으로 제거 가능.
-
정렬된 태스크의 경우, 하나의 태스크를 제거하려 하면 다른 태스크의 성능도 같이 저하되므로 학습 제거가 어려움.
3.4 CAN A MODEL PROVABLY GENERALIZE OUT-OF-DOMAIN WITH TASK ARITHMETIC?
이 섹션에서는 태스크 벡터의 선형 조합을 통해 모델이 기존 학습된 태스크를 넘어 새로운(out-of-domain) 태스크로 일반화할 수 있는지에 대한 이론적 분석을 수행한다.
선행 연구에 따르면, 태스크 벡터들은 서로 직교(orthogonal)하는 경향이 있음. 따라서, 본 연구에서는 각 태스크의 주요 특징을 나타내는 벡터들{ \mu{T_i} }{i \in V_{\Psi}}**이 직교 정규 집합(orthonormal set)이라고 가정**
-
새로운 태스크 T′ 의 판별적 패턴: \mu{T’} = \sum{i \in V{\Psi}} \gamma_i \mu{Ti} + \kappa \cdot \mu’{\perp}
-
\gamma_i \in \mathbb{R}: 기존 태스크의 판별적 패턴 μTi 에 대한 선형 가중치.
-
\mu’_{\perp}: 기존 태스크들의 판별적 패턴과 완전히 직교한(orthogonal) 새로운 구성 요소.
-
\kappa (카파): 새로운 태스크의 직교 성분 μ⊥′ 의 크기를 조절하는 계수.
-
즉, 새로운 태스크 T′ 의 판별적 패턴은 기존 태스크의 패턴들의 선형 조합( **\sum \gammai \mu{Ti}**)과, 기존 태스크와 전혀 다른 새로운 패턴( **\kappa \cdot \mu’{\perp}**)으로 구성됨.
⇒ 만약 κ=0 이면, T′는 기존 태스크들의 선형 결합으로 정확하게 표현될 수 있고, 그렇지 않으면 완전히 새로운 태스크가 됨.
Theorem 3 (도메인 외 일반화 성공 조건)
태스크 벡터를 만드는 방식은 위의 조건과 동일
모델 \Psi 가 새로운 태스크 T′에 대해 일반화 오류를 보장하기 위해서는 다음 조건을 만족해야 한다.
- (A) 적어도 하나의 기존 태스크가 새로운 태스크와 연관되어야 함
\exists i \in V_{\Psi} \text{ such that } \gamma_i \neq 0
-
즉, T′의 판별적 패턴(**\mu_{T’}**)이 기존 태스크 중 적어도 하나와 관련이 있어야 함.
-
만약 모든 \gamma_i = 0 이라면, T′는 기존 태스크들과 완전히 무관한 새로운 태스크이므로, 일반화가 어려움.
-
(B) 적절한 **\lambda_i**가 존재해야 함
\sum{i \in V{\Psi}} \lambdai \gamma_i \geq 1 + c, \quad \sum{i \in V_{\Psi}} \lambda_i \gamma_i^2 \geq 1 + c
-
즉, 각 태스크 벡터의 가중치 **\lambda_i** 들이 적절히 조정되어야 함.
-
첫 번째 조건은 태스크 T′의 주요 패턴을 충분히 반영하기 위한 제약.
-
두 번째 조건은 이진 분류에서 필요한 마진(margin)을 유지하기 위한 제약.
-
-
(C) **\lambda_i**의 크기가 너무 크지 않아야 함
| \lambda*i | \cdot \beta \leq c, \quad \forall i \in V*{\Psi} |
-
즉, 각 태스크 벡터의 가중치 λi가 너무 크면 오류가 증가할 수 있음.
-
따라서, 적절한 범위 내에서 λi를 조정해야 모델이 안정적으로 일반화됨.
위 조건이 충족되면, 새로운 태스크 T′ 에 대한 일반화 오류는 다음과 같이 유지됨:
\mathbb{E}{(X,y) \sim D{T’}} l(X, y; \Psi) \leq \Theta(\epsilon)
즉, 도메인 외 태스크에 대해 모델이 안정적인 성능을 유지할 수 있음!
3.5 CAN TASK VECTORS BE IMPLEMENTED EFFICIENTLY?
이 섹션에서는 태스크 벡터(Task Vector) 기법의 계산 효율성을 향상시키는 방법으로, Low-Rank과 Sparsity를 검토한다.
Corollary 1. *(Low-rank approximation)
-
-
태스크 벡터 ΔW_T 와 ΔV_T 는 저차원(rank-1) 근사를 사용할 수 있음.
-
여러 연구(Ilharco et al., 2022a)에서 태스크 벡터가 직교하는 경향이 있고, 대부분 특정한 방향으로 업데이트됨이 확인됨.
-
이는 rank-1 근사로도 충분한 표현이 가능함을 의미함.
-
-
저차원 근사 행렬을 ΔW_LR, ΔV_LR 라고 할 때, 다음이 성립함:
-
\Delta WT - \Delta W{LR}|_F \leq M \cdot \epsilon + \frac{1}{\log M} -
M 은 데이터 차원의 크기이며, 학습 중 특정 방향으로 업데이트가 이루어지기 때문에 오차가 M 에 비례할 수 있음.
-
\epsilon 은 태스크 벡터의 일반화 오류를 나타내며, 이 값이 작을수록 모델이 잘 학습됨.
-
l**\frac{1}{logM}** 항목
-
저차원 근사는 데이터 차원이 클수록 더 잘 작동하는 경향이 있음.
-
즉, M 이 커질수록 근사 오류가 로그 스케일로 감소함.
-
-
-
|\Delta VT - \Delta V{LR}|_F \leq \delta^{-1} \epsilon
-
δ^{−1}ϵ 항목은 태스크 벡터가 특정 패턴을 얼마나 잘 학습했는지를 반영함.
-
δ 는 태스크의 판별적 패턴이 데이터에서 차지하는 비율을 나타내며, δ 가 클수록 모델이 해당 태스크를 더 잘 학습할 수 있음.
-
따라서, \delta^{-1}는 태스크의 학습 가능성을 나타내는 척도로 볼 수 있으며, 이 값이 크면 rank-1 근사가 더 어려워지고 오차가 증가할 가능성이 있음.
-
태스크의 판별적 패턴 비율 δ가 충분히 크다면, rank-1 근사로 인해 발생하는 오차는 작게 유지될 수 있음.
-
-
즉, 저차원 근사로 인해 발생하는 오차가 매우 작다는 것을 보장.
이 결과가 의미하는 바는 다음과 같다.
-
태스크 벡터는 본질적으로 저차원 구조를 가지며, rank-1 근사를 적용해도 성능을 유지할 수 있다.
-
태스크 벡터의 근사 오차는 데이터 차원( M)과 학습 정도(δ에 의해 결정됨.
-
데이터 차원 M 이 크면 rank-1 근사로 인한 오차가 로그 스케일로 감소함.
-
δ값이 크면 태스크 벡터의 주요 패턴을 더 잘 유지할 수 있음.
- 연산량을 줄이면서도 모델 성능을 유지하는 최적화 전략으로 활용 가능.
- 모델을 경량화하는 데 유용하며, 메모리 사용량 감소 및 계산 비용 절감 가능.
Corollary 2. *(Sparsity of task vectors)
-
Corollary 2에서는 태스크 벡터 **\Delta V_T^* 의 희소성을 수학적으로 증명**한다.
-
태스크 벡터 \Delta V_T^*의 각 행 u_i에 대해 다음이 성립:
- 중요한 행들( **i \in L**)
| u_i | \geq \Omega(m^{-1/2})
- 이 행들은 **상대적으로 큰 가중치를 가지며 중요한 정보를 포함**.
- 즉, **모델이 특정 태스크를 학습할 때 중요하게 업데이트된 가중치들**.
- 불필요한 행들(** i \in [m] \setminus L**)
| u_i | \leq O(m^{-1/2} \sqrt{\log B / B})
- 이 행들은 **가중치 값이 매우 작아서 중요하지 않은 정보만 포함**.
- 배치 크기(B) 가 커질수록 불필요한 행들의 가중치는 더욱 작아짐.
- 즉, **모델이 학습할 때 거의 업데이트되지 않은 가중치들**.
-
결과: 불필요한 행을 제거(Pruning)해도 괜찮음!
-
즉, 태스크 벡터의 일부 요소를 제거해도 멀티태스크 학습, 학습 제거, 도메인 외 일반화 성능이 유지됨.
-
모델이 중요한 정보만 남겨놓고 불필요한 가중치를 제거해도 문제없이 작동할 수 있다.
-
4. NUMERICAL EXPERIMENTS
4.1 EXPERIMENTS ON IMAGE CLASSIFICATION
Experiment Setup
-
사용한 모델:
-
ViT-Small/16
-
ImageNet-21K로 사전 학습된 모델을 사용하여 fine-tuning 진행.
-
-
사용한 데이터셋:
-
Colored-MNIST
-
이진 분류(binary classification) 태스크에서 숫자의 홀수/짝수를 분류하는 문제로 실험 수행.
-
숫자의 색상(빨강/초록)을 조작하여 태스크 간 상관관계(irrelevant, aligned, contradictory)를 조정.
-
Define ro and re as the proportion of red colors in odd and even digits
-
-
태스크 간 상관관계 측정 방법:
- 두 개의 태스크 T1,T2 가 각각 미세 조정된 모델 ΨT1∗, ΨT2∗ 의 출력을 기반으로 출력 벡터 간 코사인 유사도(Cosine Similarity)를 평균하여 상관관계 α를 계산.
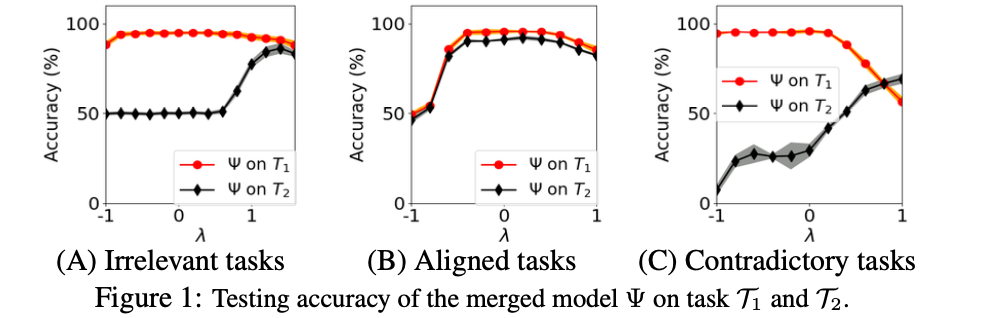
Multitask & Unlearning
-
태스크 간 상관관계가 다른 3가지 경우를 비교:
-
Case I (무관한 태스크, **\alpha \approx 0**) → 0.164
-
Case II (정렬된 태스크, α>0) → 0.891
-
Case III (상충하는 태스크, α<0) → −0.849
-
-
결과:
-
무관한 태스크
-
λ≥1→ 멀티태스크 학습 성공
-
λ≤0 → 특정 태스크 제거 성공
-
-
정렬된 태스크
-
λ>0→ 두 태스크 모두 성능 증가
-
하지만 λ 의 어떤 값도 한 태스크를 제거하면서 다른 태스크를 유지할 수 없음
-
-
상충하는 태스크( α<0 )
-
λ≤0 → 특정 태스크 제거 성공
-
멀티태스크 학습은 불가능
-
-
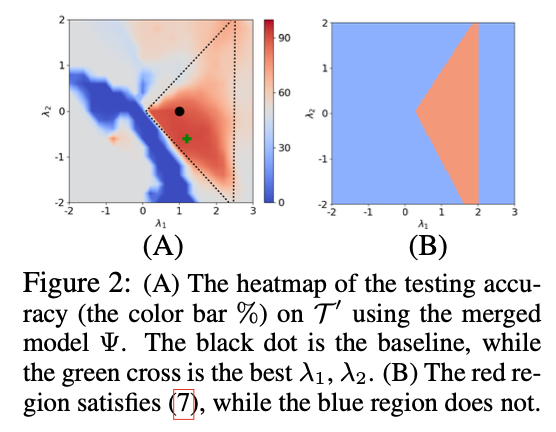
OOD
-
T1 (ro = 0.85), T2 (ro = 0.05), 목표 태스크 T′(ro = 0.9)
-
T1,T2 는 **무관한 태스크 **
-
특정 λ1,λ2 의 삼각형 영역 내에서 도메인 외 일반화 가능
-
Theorem 3에서 제시한 조건 (7)과 일치하는 영역에서 좋은 성능을 보임!
4.2 EXPERIMENT ON LANGUAGE GENERATION TASK
-
사용한 모델:
- Phi-1.5 (1.3B) 모델
-
사용한 데이터셋:
-
Harry Potter 1 (HP1), Harry Potter 2 (HP2) → 정렬된(aligned) 태스크 (α=0.498)
-
Pride and Prejudice (PP) → HP1과 덜 정렬됨 (α=0.239)
-
-
실험 목표:
-
학습 제거(Unlearning) 테스트
-
HP1을 제거하면 HP2와 PP의 성능이 어떻게 변화하는지 분석
-
-
성능 측정:
- Rouge-L Score 사용
-
결과:
-
λ<0 로 HP1을 제거하면, HP2도 함께 성능 저하됨.
-
PP는 상대적으로 덜 영향을 받음.
-
Theorem 2의 예측과 일치!
-
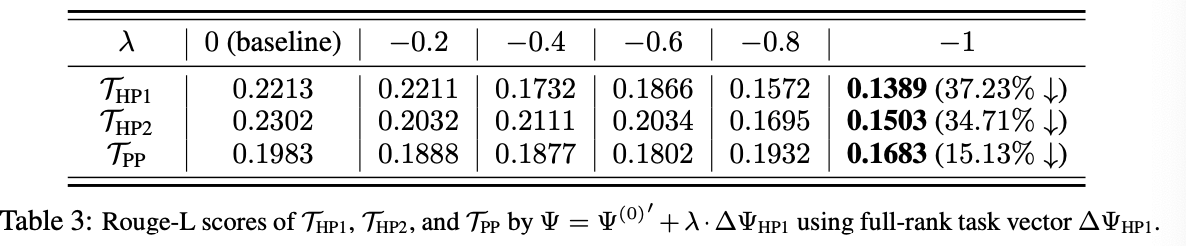
- LoRA 사용 시에도 같은 결과가 유지됨 → Corollary 1 검증!

최종 요약
-
이미지 분류 실험에서, 멀티태스크 학습 및 학습 제거가 태스크 간 상관관계에 따라 다르게 작동하는 것이 확인됨 (Theorem 1, 2 검증).
-
도메인 외 일반화 실험에서도 Theorem 3의 조건이 실험적으로 검증됨.
-
자연어 생성 실험에서, 특정 태스크를 제거하면 정렬된 태스크도 함께 성능이 저하됨 (Theorem 2 검증).
-
LoRA를 적용해도 동일한 패턴을 보이며, Corollary 1(저차원 근사)도 검증됨!